👀个人简介:一个正在努力奋斗逆天改命的二本觉悟生
前言:这篇博客将给大家讲解二叉树的做题小技巧和思路,大家可以先做一遍,再看看答案是否正确,巩固一下
目录
二叉树选择题
二叉树性质:
对任何一棵⼆叉树, 如果度为 0 其叶结点个数为 n 0 , 度为 2 的分支结点个数为 n 2 ,则有n 0 = n 2 + 1
推理过程:
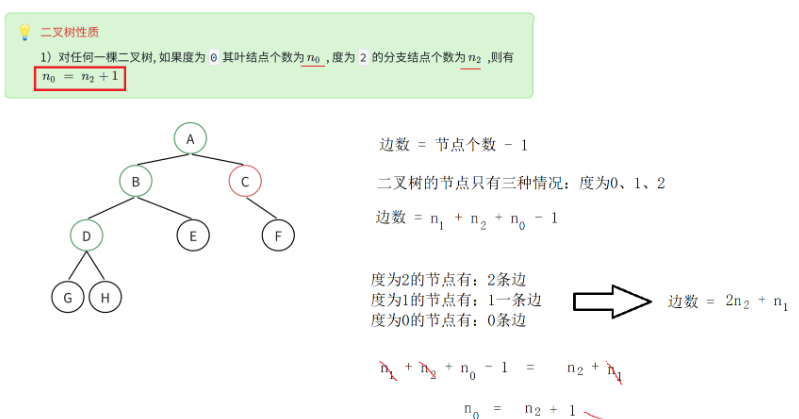
假设一个二叉树有 n2个度为2的节点, n1个度为1的节点, n0个叶节点,则这个二叉树的边数是
2n2+n1 另一方面,由于共有 n2+n0+n1 个节点,所以边数等于 n2+n0+n1-1
结合以上两个公式:
2n2+n1 = n2+n0+n1-1 ,即: n0=n2+1
二叉树的性质选择题:
1.某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为(B)
A.不存在这样的二叉树 B.200 C.198 D.199
由于二叉树的性质,n0=n2+1,因为度为2的节点个数为199个,所以n0=199+1=200,即叶子节点个数为200
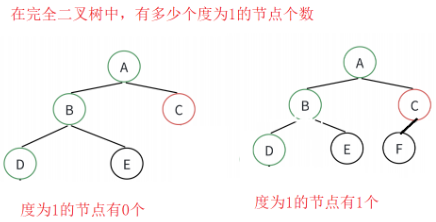
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A)
A.n B.n+1 C.n-1 D.n/2
在完全二叉树中不存在度为1的节点右两个的情况(完全二叉树的性质)
2n=n1+n2+n0
n0=2n-n1-n2因为n0=n2+1
n2+1=2n-n1-n2
2n0=2n-n1+1
完全二叉树里,度为1的节点要么为0,要么为1,所以将0带入,发现n0为分数,所以排除,将1带入,n0=n
3.⼀棵完全二叉树的结点数为531个,那么这棵树的高度为(B)
A.11 B.10 C.8 D.12
前9层节点总个数=2^9-1= 511
我们这个完全二叉树的结点个数为531,所以高度是有10层,且最后一层的结点个数(叶子结点个数)为531-511=20个。
4.⼀个具有767个结点的完全二叉树,其叶子结点个数为(B)
A.383 B.384 C.385 D.386
n0+n1+n2=767 且n2=n0-1
所以n0+n0+n1-1=767
完全二叉树中总结点个数为奇数个(出来头节点剩下全为偶数),所以n1为0
故2n0=768 n0=384
综上所述,叶子结点个数为384个
链式二叉树的遍历选择题:
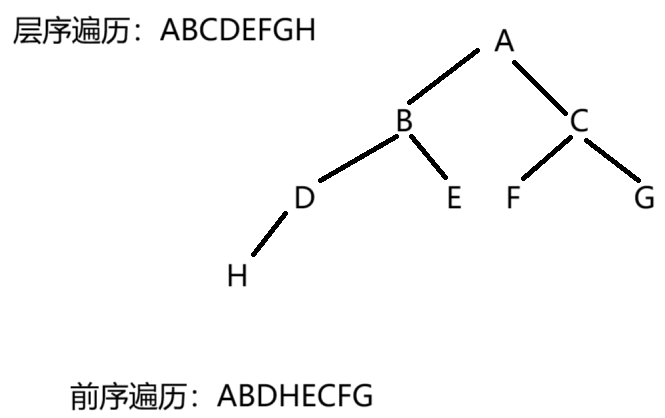
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为(A)
A. ABDHECFG
B. ABCDEFGH
C. HDBEAFCG
D. HDEBFGCA
先根据层序遍历序列画出这颗树,然后再通过画出来的树求出它的前序遍历序列
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为(A)
A. E
B. F
C. G
D. H
先序遍历就是前序遍历其第一个结点肯定就是根结点,所以这题根节点就是E可以直接选A。
补充一下,如果是后序遍历的话根结点一定是最后一个结点。中序遍历的话左右孩子结点分别在根节点两侧(具体是那两个需要确定)。
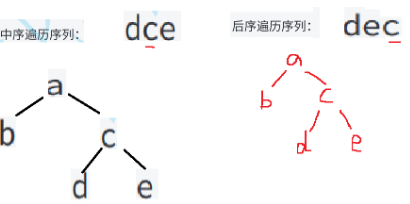
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为(D)
A. adbce
B. decab
C. debac
D. abcde
根据后序遍历,我们可以确定根节点为a,根据中序遍历,左边除了b就没有了所以b肯定为a的左孩子结点,dce为a的右孩子,所以c就是a的右孩子,d为c的左孩子,e为c的右孩子
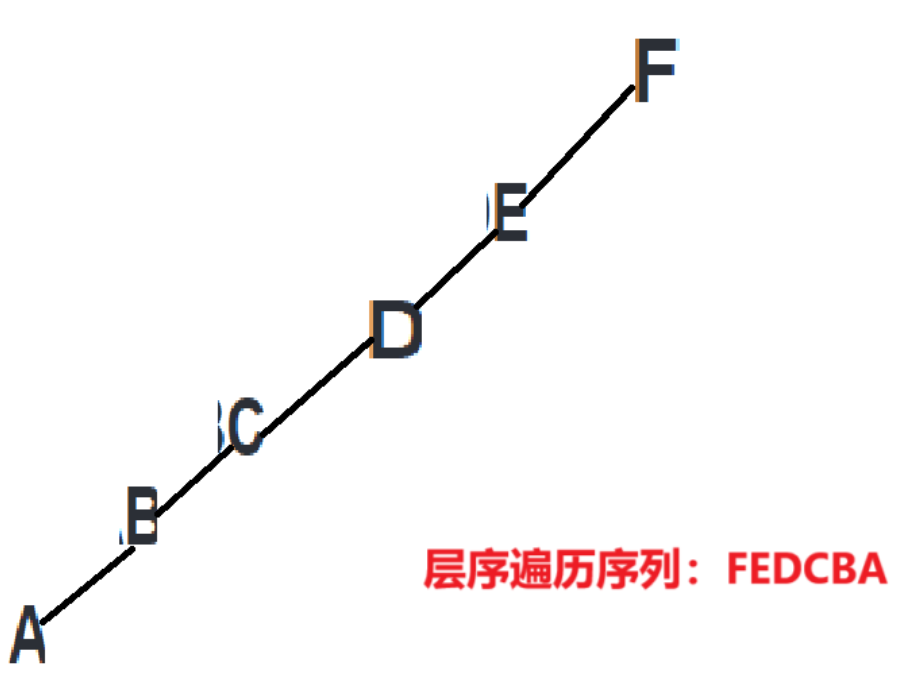
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同⼀层从左到右的序列为(A)
A. FEDCBA
B. CBAFED
C. DEFCBA
D. ABCDEF
和上道题的思路一样,还是根据后序遍历确定根节点,在判断左右孩子即可,如图:
往期回顾:
总结:二叉树的全部内容到此为止就结束了,总体来说难度较顺序表、链表、栈和队列大了一点,后续大家多加复习,接着我会在我的LeetCode刷题集更新二叉树的相关题解,大家可以关注一下,如果文章对你有帮助的话,欢迎评论,点赞,收藏加关注,感谢大家的支持。