leetcode_73 矩阵置零

1. 题意

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

2. 题解

想不到O(1)的空间复杂度的做法，

只有抄抄题解这样子才能维持的了生活。

2.1 暴力

维护两个标记数组，分别表示某行或者某列有0。

时间复杂度$O(n)$

空间复杂度$O(n)$

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        // row column flag

        int r = matrix.size();
        int c = 0;
        if ( r )
            c = matrix[0].size();

        vector<int> row_flags(r, 0);
        vector<int> col_flags(c, 0);

        for (int i = 0;i < r; ++i) {
            for (int j = 0;j < c; ++j) {
                if (0 == matrix[i][j]) {
                    row_flags[i] = col_flags[j] = 1;
                }
            }
        }


        for (int i = 0;i < r; ++i) {
            for (int j = 0; j < c; ++j) {
                if (row_flags[i] || col_flags[j])
                    matrix[i][j] = 0;
            }
        }
    }
};

2.2 原地算法

用数组的第一行和第一列分别来表示，某一列或者某一行它有0。

我们用0来表示有0，因为这样就不用考虑第0行和第0列的情况了。

在用0行和第0列表示之前， 我们需要用两个变量先预处理出第0行

和第0列的情况。

其实就是

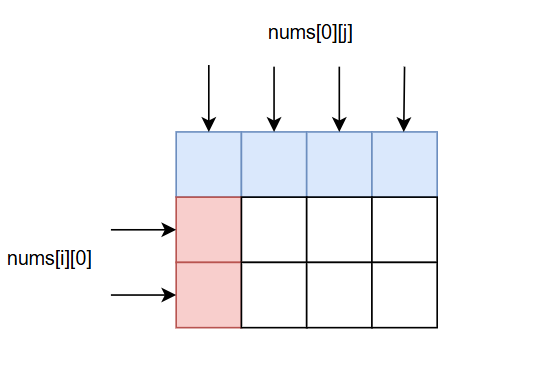
用nums[i][0]表示第i行有没有0；

用nums[0][j]表示第j列有没有0；

其中0<i<rows,0<j<cols

而第0行和第0列就用first_col first_rol单独进行判断了。

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        // row column flag

        int r = matrix.size();
        int c = 0;
        if ( 0 != r)
            c = matrix[0].size();

        int first_col = 0;
        int first_row = 0;

        for (int i = 0;i < c; ++i) {
            if ( matrix[0][i] == 0) {
                first_row = 1;
                break;
            }
        }

        for (int i = 0; i < r; ++i) {
            if ( matrix[i][0] == 0) {
                first_col = 1;
                break;
            }
        }

        for (int i = 1; i < r; ++i) {
            for (int j = 1; j < c; ++j) {
                if ( matrix[i][j] == 0) {
                    matrix[0][j] = 0;
                    matrix[i][0] = 0;
                }   
            }
        }


        for (int i = 1; i < r; ++i) {
            for (int j = 1; j < c; ++j) {
                if (matrix[0][j] == 0 || matrix[i][0] == 0)
                    matrix[i][j] = 0;
            }
        }


        if (first_col) {
            for (int i = 0;i < r; ++i)
                matrix[i][0] = 0;
        }
        if (first_row) {
            for (int i = 0;i < c; ++i)
                matrix[0][i] = 0;
        }

    }
};

而题解中维护一个变量的做法，

其实就是把nums[0][0]这个位置再拿去

表示第0行有0或者第0列有0从而省略掉一个变量。

但这样做其实增加了复杂度，以nums[0][0]表示第0列有无0来说。

对于nums[0][j]=0 , j>0来说，它不能引起nums[0][0]的更新，

因为nums[0][0]表示的是第0列的状况，而不是第0行的状况了。

因此需要加一个判断了。

其次在最后遍历数组的时候，我们需要逆序的列遍历了。

因为如果顺序的话nums[i][0]表示的行信息就被覆盖掉了。

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        // row column flag

        int r = matrix.size();
        int c = 0;
        if ( 0 != r)
            c = matrix[0].size();

        int first_row = 0;

        for (int i = 0;i < c; ++i) {
            if ( matrix[0][i] == 0) {
                first_row = 1;
                break;
            }
        }


        for (int i = 0; i < r; ++i) {
            for (int j = 0; j < c; ++j) {
                if ( matrix[i][j] == 0) {
                    matrix[0][j] = 0;
                    if ( i != 0 )
                        matrix[i][0] = 0;
                }   
            }
        }
       
        for (int i = 1; i < r; ++i) {

             // be carefull here, we need traversal reverse order
            for (int j = c - 1; ~j; --j) {
                if (matrix[0][j] == 0 || matrix[i][0] == 0)
                    matrix[i][j] = 0;
            }
        }
        if (first_row) {
            for (int i = 0;i < c; ++i)
                matrix[0][i] = 0;
        }

    }
};

如果用nums[0][0]表示第0行的状况也是相似的，代码也给出来吧。

class Solution {
public:
    void setZeroes(vector<vector<int>>& matrix) {
        // row column flag

        int r = matrix.size();
        int c = 0;
        if ( 0 != r)
            c = matrix[0].size();

        int first_col = 0;

        for (int i = 0;i < r; ++i) {
            if ( matrix[i][0] == 0) {
                first_col = 1;
                break;
            }
        }


        for (int i = 0; i < r; ++i) {
            for (int j = 0; j < c; ++j) {
                if ( matrix[i][j] == 0) {
                    matrix[i][0] = 0;
                    if (j != 0)
                        matrix[0][j] = 0;
                }   
            }
        }

       
        for (int i = r - 1; ~i; --i) {
            for (int j = 1;j < c; ++j) {
                if ( matrix[0][j] == 0 || matrix[i][0] == 0 ) {
                    matrix[i][j] = 0;
                }
            }
        }


        if (first_col) {
            for (int i = 0;i < r; ++i)
                matrix[i][0] = 0;
        }

    }
};

空间复杂度$O(1)$

3. 参考

leetcode