【数据结构】图

图

图的概念

定义: 图是由顶点集合 (V) 和顶点间的关系 (边) 集合 (E) 组成的一种数据结构 ，记作 G=(V,E)。

图的分类：

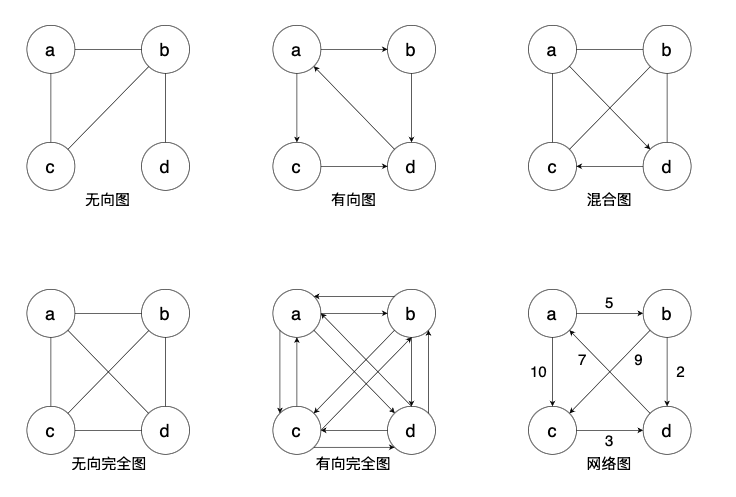
• 无向图：顶点对 <x, y> 是无序（无向边）的图
• 有向图：顶点对 <x, y> 是有序（有向边）的图
• 混合图：既有无向边也有有向边的图
• 完全图：
  • 有 n 个顶点的无向图有 $\frac{n(n-1)}{2}$ 条边，则此图称为无向完全图
  • 有 n 个顶点的有向图有 $n(n-1)$ 条边，则此图称为有向完全图
• 加权图 (网络)：边的关系带有数值（权），例如距离、耗时等

邻接顶点: 有边连接的两个顶点互为邻接顶点

关联边： 若边 e= (v, u)，则称边 e 和顶点 v、u 相关联

子图： 设有两个图 $G＝(V,E)$ 和 $G‘＝(V’,E^{\prime })$。若 $V’\subseteq V$ 且 $E^{\prime }\subseteq E$, 则称 图 $G’$ 是图 $G$ 的子图

权： 某些图的边具有与它相关的数，称之为权，这种带权图叫做网络

顶点的度: 无向图中与该顶点相连的边数 。在有向图中，分为入度（指向该顶点的弧的数目）和出度（从该顶点发出的弧的数目），顶点的度 = 出度 + 入度

路径长度： 非带权图的路径长度是指此路径上边的条数。带权图的路径长度是指路径上各边的权之和

简单路径 ： 若路径上各顶点 v1,v2,…,vm 均不 互相重复, 则称这样的路径为简单路径

简单回路： 若路径上第一个顶点 v1 与最后一个顶点vm 重合, 则称这样的路径为回路或环。

连通图: 在无向图中，任意两个顶点之间都有路径相通；非连通图的极大连通子图叫做连通分量

强连通图: 在有向图中，任意一对顶点 v_i 和 v_j，都存在从 v_i 到 v_j 和从 v_j 到 v_i 的路径；非强连通图的极大强连通子图叫做强连通分量

图的存储结构

邻接矩阵 (Adjacency Matrix)

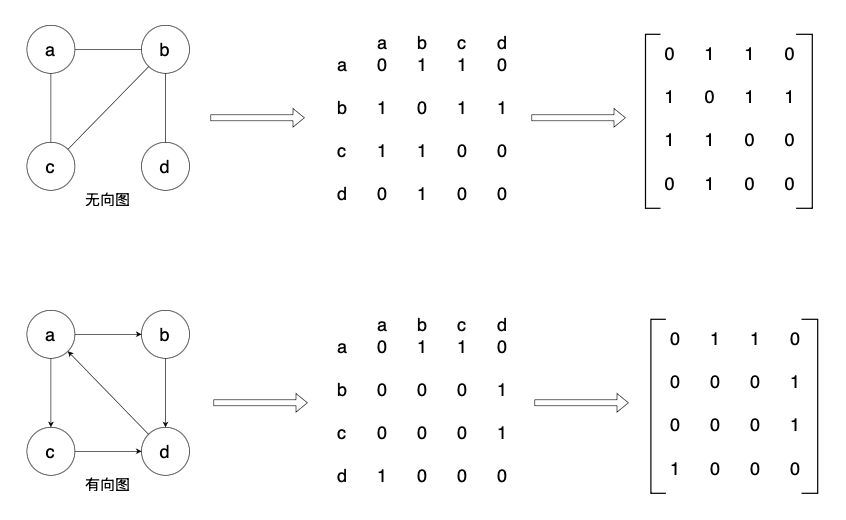
邻接矩阵通常用一个二维数组来表示，其基本思想是 G.arcs[i][j] 的值表示顶点 i 到顶点 j 之间的关系。这个值可以是布尔值（0 或 1），也可以是边的权值。

1. 图的结构定义

   首先，需要定义一个结构体来表示图，其中包含顶点数组、邻接矩阵和顶点的数量。

   #define MAX_VERTEX_NUM 20 // 最大顶点数
   typedef char VertexType; // 顶点的数据类型
   
   // 图的结构体
   typedef struct {
       VertexType Vex[MAX_VERTEX_NUM]; // 顶点数组
       int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵
       int vexnum, arcnum; // 图的顶点数和边数
   } MGraph;
   

   • Vex：存储图中的所有顶点。
   • arcs：核心的邻接矩阵，arcs[i][j] 为 1 表示顶点 i 到 j 有边，为 0 表示无边。对于带权图，这里可以存储权值。
   • vexnum：记录当前图的顶点数量。
   • arcnum：记录当前图的边数量。

2. 创建图的函数

   这个函数会提示用户输入图的顶点和边的信息，并构建邻接矩阵。

   #include <stdio.h>
   
   // 创建一个无向图的邻接矩阵
   void CreateMGraph(MGraph *G) {
       int i, j, k;
       printf("请输入图的顶点数和边数，用空格分隔：\n");
       scanf("%d %d", &G->vexnum, &G->arcnum);
   
       printf("请输入所有顶点的值：\n");
       for (i = 0; i < G->vexnum; ++i) {
           scanf(" %c", &G->Vex[i]); // 注意前面的空格，用于跳过空白符
       }
   
       // 初始化邻接矩阵，所有边都设为0
       for (i = 0; i < G->vexnum; ++i) {
           for (j = 0; j < G->vexnum; ++j) {
               G->arcs[i][j] = 0;
           }
       }
   
       printf("请依次输入每条边的两个顶点（例如：v1 v2）：\n");
       for (k = 0; k < G->arcnum; ++k) {
           char v1, v2;
           int p1, p2;
           scanf(" %c %c", &v1, &v2);
   
           // 查找顶点在数组中的索引
           for (i = 0; i < G->vexnum; ++i) {
               if (G->Vex[i] == v1) {
                   p1 = i;
               }
               if (G->Vex[i] == v2) {
                   p2 = i;
               }
           }
   
           // 设置邻接矩阵的值
           G->arcs[p1][p2] = 1;
           G->arcs[p2][p1] = 1; // 因为是无向图
       }
   }
   

3. 打印邻接矩阵

   这个函数可以帮助直观地看到生成的邻接矩阵，便于验证。

   // 打印邻接矩阵
   void PrintMGraph(MGraph G) {
       int i, j;
       printf("\n邻接矩阵如下：\n");
       // 打印列索引
       printf("  ");
       for(i = 0; i < G.vexnum; ++i) {
           printf("%c ", G.Vex[i]);
       }
       printf("\n");
   
       for (i = 0; i < G.vexnum; ++i) {
           // 打印行索引
           printf("%c ", G.Vex[i]);
           for (j = 0; j < G.vexnum; ++j) {
               printf("%d ", G.arcs[i][j]);
           }
           printf("\n");
       }
   }
   

4. 主函数和完整代码

   将上面的函数组合起来，可以创建一个完整的程序来演示邻接矩阵的实现。

   #include <stdio.h>
   
   #define MAX_VERTEX_NUM 20
   typedef char VertexType;
   
   // 图的结构体定义 (同上)
   typedef struct {
       VertexType Vex[MAX_VERTEX_NUM];
       int arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM];
       int vexnum, arcnum;
   } MGraph;
   
   // 创建图的函数 (同上)
   void CreateMGraph(MGraph *G) {
       int i, j, k;
       printf("请输入图的顶点数和边数，用空格分隔：\n");
       scanf("%d %d", &G->vexnum, &G->arcnum);
   
       printf("请输入所有顶点的值：\n");
       for (i = 0; i < G->vexnum; ++i) {
           scanf(" %c", &G->Vex[i]);
       }
   
       for (i = 0; i < G->vexnum; ++i) {
           for (j = 0; j < G->vexnum; ++j) {
               G->arcs[i][j] = 0;
           }
       }
   
       printf("请依次输入每条边的两个顶点（例如：A B）：\n");
       for (k = 0; k < G->arcnum; ++k) {
           char v1, v2;
           int p1 = -1, p2 = -1;
           scanf(" %c %c", &v1, &v2);
   
           for (i = 0; i < G->vexnum; ++i) {
               if (G->Vex[i] == v1) p1 = i;
               if (G->Vex[i] == v2) p2 = i;
           }
   
           if (p1 != -1 && p2 != -1) {
               G->arcs[p1][p2] = 1;
               G->arcs[p2][p1] = 1;
           }
       }
   }
   
   // 打印邻接矩阵函数 (同上)
   void PrintMGraph(MGraph G) {
       int i, j;
       printf("\n邻接矩阵如下：\n");
       printf("  ");
       for(i = 0; i < G.vexnum; ++i) {
           printf("%c ", G.Vex[i]);
       }
       printf("\n");
   
       for (i = 0; i < G.vexnum; ++i) {
           printf("%c ", G.Vex[i]);
           for (j = 0; j < G.vexnum; ++j) {
               printf("%d ", G.arcs[i][j]);
           }
           printf("\n");
       }
   }
   
   int main() {
       MGraph G;
       CreateMGraph(&G);
       PrintMGraph(G);
       return 0;
   }
   

• 使用一个二维数组表示顶点间的关系
• 优点: 易于实现图的操作，如判断顶点是否邻接、求顶点的度等
• 缺点: 空间复杂度为O(n²)，对于顶点数多的稀疏图会造成空间浪费

邻接表 (Adjacency List)

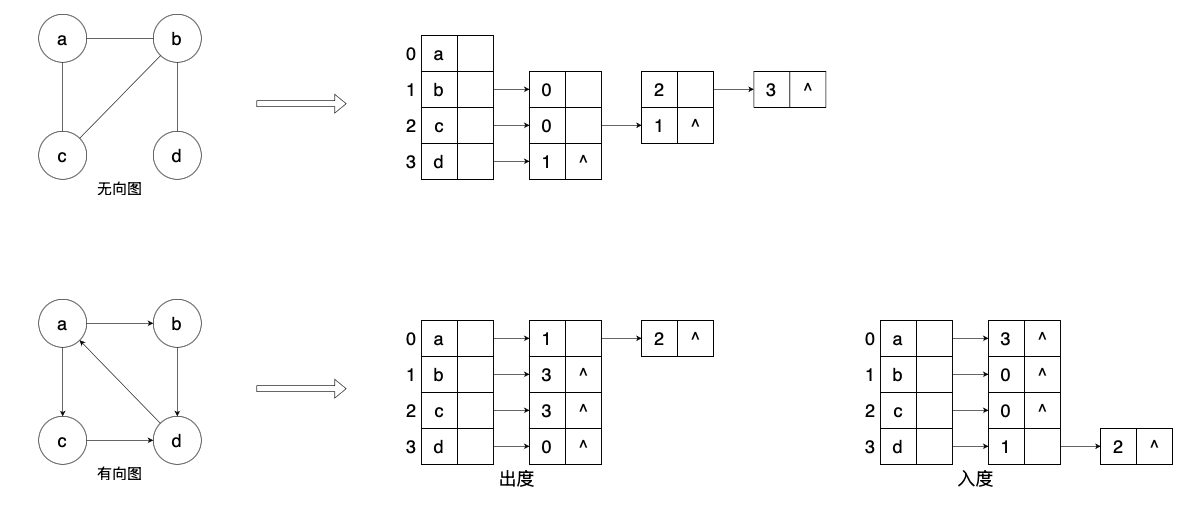
邻接表是另一种重要的图存储结构，它比邻接矩阵更节省空间，尤其适用于稀疏图。其核心思想是为每个顶点维护一个链表，链表中的节点存储与该顶点相连的其他顶点及其边的信息。

1. 图的结构定义

   邻接表的实现需要两个核心结构体：一个用于表示边上的节点，另一个用于表示图本身。

   #define MAX_VERTEX_NUM 20
   typedef char VertexType; // 顶点的数据类型
   
   // 边表节点
   typedef struct ArcNode {
       int adjvex; // 邻接点在顶点数组中的索引
       struct ArcNode *nextarc; // 指向下一个邻接点
   } ArcNode;
   
   // 顶点表节点
   typedef struct VNode {
       VertexType data; // 顶点信息
       ArcNode *firstarc; // 指向该顶点所连的第一个邻接点
   } VNode, AdjList[MAX_VERTEX_NUM];
   
   // 图的结构体
   typedef struct {
       AdjList vertices; // 邻接表
       int vexnum, arcnum; // 图的顶点数和边数
   } ALGraph;
   

   • ArcNode: 边表节点，用于存储邻接点在顶点数组中的索引，以及指向下一个边表节点的指针。
   • VNode: 顶点表节点，用于存储顶点数据和指向其第一个邻接点的指针。
   • AdjList: 实际上是一个VNode数组，即邻接表的主体。
   • ALGraph: 包含邻接表和图的顶点数、边数等信息。

2. 创建图的函数

   这个函数会提示用户输入图的顶点和边的信息，并构建邻接表。

   #include <stdio.h>
   #include <stdlib.h> // 需要用到malloc
   
   // 创建一个无向图的邻接表
   void CreateALGraph(ALGraph *G) {
       int i, k;
       printf("请输入图的顶点数和边数，用空格分隔：\n");
       scanf("%d %d", &G->vexnum, &G->arcnum);
   
       printf("请输入所有顶点的值：\n");
       for (i = 0; i < G->vexnum; ++i) {
           scanf(" %c", &G->vertices[i].data);
           G->vertices[i].firstarc = NULL; // 初始化边表头指针
       }
   
       printf("请依次输入每条边的两个顶点（例如：v1 v2）：\n");
       for (k = 0; k < G->arcnum; ++k) {
           char v1, v2;
           int p1 = -1, p2 = -1;
           scanf(" %c %c", &v1, &v2);
   
           // 查找顶点在数组中的索引
           for (i = 0; i < G->vexnum; ++i) {
               if (G->vertices[i].data == v1) p1 = i;
               if (G->vertices[i].data == v2) p2 = i;
           }
   
           if (p1 == -1 || p2 == -1) continue;
   
           // 无向图，需要分别创建两个边表节点
           // 创建p2到p1的边
           ArcNode *p2_to_p1 = (ArcNode *)malloc(sizeof(ArcNode));
           p2_to_p1->adjvex = p1;
           p2_to_p1->nextarc = G->vertices[p2].firstarc;
           G->vertices[p2].firstarc = p2_to_p1;
   
           // 创建p1到p2的边
           ArcNode *p1_to_p2 = (ArcNode *)malloc(sizeof(ArcNode));
           p1_to_p2->adjvex = p2;
           p1_to_p2->nextarc = G->vertices[p1].firstarc;
           G->vertices[p1].firstarc = p1_to_p2;
       }
   }
   

   • CreateALGraph 函数首先初始化每个顶点的边表头指针为NULL。
   • 然后，对于每条输入的边，它会创建两个ArcNode，一个用于添加到v1的邻接链表中，另一个用于添加到v2的邻接链表中。这里使用了“头插法”来添加节点，因此新节点会插入到链表的头部。

3. 打印邻接表

   这个函数可以看到生成的邻接表的结构。

   // 打印邻接表
   void PrintALGraph(ALGraph G) {
       int i;
       printf("\n邻接表如下：\n");
       for (i = 0; i < G.vexnum; ++i) {
           printf("%c: ", G.vertices[i].data);
           ArcNode *p = G.vertices[i].firstarc;
           while (p) {
               printf("->%c ", G.vertices[p->adjvex].data);
               p = p->nextarc;
           }
           printf("\n");
       }
   }
   

4. 主函数和完整代码

   #include <stdio.h>
   #include <stdlib.h>
   
   #define MAX_VERTEX_NUM 20
   typedef char VertexType;
   
   // 边表节点 (同上)
   typedef struct ArcNode {
       int adjvex;
       struct ArcNode *nextarc;
   } ArcNode;
   
   // 顶点表节点 (同上)
   typedef struct VNode {
       VertexType data;
       ArcNode *firstarc;
   } VNode, AdjList[MAX_VERTEX_NUM];
   
   // 图的结构体 (同上)
   typedef struct {
       AdjList vertices;
       int vexnum, arcnum;
   } ALGraph;
   
   // 创建图的函数 (同上)
   void CreateALGraph(ALGraph *G) {
       int i, k;
       printf("请输入图的顶点数和边数，用空格分隔：\n");
       scanf("%d %d", &G->vexnum, &G->arcnum);
   
       printf("请输入所有顶点的值：\n");
       for (i = 0; i < G->vexnum; ++i) {
           scanf(" %c", &G->vertices[i].data);
           G->vertices[i].firstarc = NULL;
       }
   
       printf("请依次输入每条边的两个顶点（例如：A B）：\n");
       for (k = 0; k < G->arcnum; ++k) {
           char v1, v2;
           int p1 = -1, p2 = -1;
           scanf(" %c %c", &v1, &v2);
   
           for (i = 0; i < G->vexnum; ++i) {
               if (G->vertices[i].data == v1) p1 = i;
               if (G->vertices[i].data == v2) p2 = i;
           }
   
           if (p1 != -1 && p2 != -1) {
               ArcNode *p1_to_p2 = (ArcNode *)malloc(sizeof(ArcNode));
               p1_to_p2->adjvex = p2;
               p1_to_p2->nextarc = G->vertices[p1].firstarc;
               G->vertices[p1].firstarc = p1_to_p2;
   
               ArcNode *p2_to_p1 = (ArcNode *)malloc(sizeof(ArcNode));
               p2_to_p1->adjvex = p1;
               p2_to_p1->nextarc = G->vertices[p2].firstarc;
               G->vertices[p2].firstarc = p2_to_p1;
           }
       }
   }
   
   // 打印邻接表函数 (同上)
   void PrintALGraph(ALGraph G) {
       int i;
       printf("\n邻接表如下：\n");
       for (i = 0; i < G.vexnum; ++i) {
           printf("%c: ", G.vertices[i].data);
           ArcNode *p = G.vertices[i].firstarc;
           while (p) {
               printf("->%c ", G.vertices[p->adjvex].data);
               p = p->nextarc;
           }
           printf("\n");
       }
   }
   
   int main() {
       ALGraph G;
       CreateALGraph(&G);
       PrintALGraph(G);
       return 0;
   }
   

• 采用链式存储结构
• 优点: 空间复杂度为O(n+e)，适用于存储稀疏图
• 缺点: 在有向图中，不易找到指向该顶点的弧

十字链表 (Cross-Linked List)

十字链表（Orthogonal List）是针对于有向图的一种更高级的链式存储结构。它能够有效地表示图中的边，并方便地找到每个顶点的出边（Outgoing Arcs）和入边（Incoming Arcs），从而解决邻接表在查找入边时效率低下的问题。

其核心思想是：

• 每个顶点有一个独立的表头节点，用于存储该顶点的信息和指向其第一条出边和入边的指针。
• 每条边（弧）都对应一个节点，该节点既挂在弧尾顶点的出边链表中，又挂在弧头顶点的入边链表中。

1. 图的结构定义

   首先，需要定义两种类型的节点：ArcNode（边节点）和 VexNode（顶点节点），以及表示图的 OLGraph 结构。

   #include <stdio.h>
   #include <stdlib.h>
   
   #define MAX_VERTEX_NUM 20
   typedef char VertexType;
   
   // 边表节点 (ArcNode)
   typedef struct ArcNode {
       int tailvex, headvex; // 弧尾和弧头在顶点数组中的索引
       struct ArcNode *hlink; // 指向下一个弧头相同的边节点
       struct ArcNode *tlink; // 指向下一个弧尾相同的边节点
   } ArcNode;
   
   // 顶点表节点 (VexNode)
   typedef struct VexNode {
       VertexType data; // 顶点信息
       ArcNode *firstin, *firstout; // 指向该顶点的第一条入边和出边
   } VexNode;
   
   // 图的结构体
   typedef struct {
       VexNode xlist[MAX_VERTEX_NUM]; // 顶点数组，即十字链表
       int vexnum, arcnum; // 图的顶点数和边数
   } OLGraph;
   

2. 创建图的函数

   这个函数会提示用户输入有向图的顶点和边的信息，并构建十字链表。

   // 创建一个有向图的十字链表
   void CreateOLGraph(OLGraph *G) {
       int i, k;
       printf("请输入有向图的顶点数和边数，用空格分隔：\n");
       scanf("%d %d", &G->vexnum, &G->arcnum);
   
       printf("请输入所有顶点的值：\n");
       for (i = 0; i < G->vexnum; ++i) {
           scanf(" %c", &G->xlist[i].data);
           G->xlist[i].firstin = NULL;
           G->xlist[i].firstout = NULL;
       }
   
       printf("请依次输入每条有向边的两个顶点（例如：v1 v2，表示从v1到v2）：\n");
       for (k = 0; k < G->arcnum; ++k) {
           char v1, v2;
           int p1 = -1, p2 = -1;
           scanf(" %c %c", &v1, &v2);
   
           // 查找弧尾和弧头顶点在数组中的索引
           for (i = 0; i < G->vexnum; ++i) {
               if (G->xlist[i].data == v1) p1 = i; // 弧尾索引
               if (G->xlist[i].data == v2) p2 = i; // 弧头索引
           }
           if (p1 == -1 || p2 == -1) continue;
   
           // 创建新的边节点
           ArcNode *new_arc = (ArcNode *)malloc(sizeof(ArcNode));
           if (new_arc == NULL) {
               printf("内存分配失败！\n");
               return;
           }
   
           // 填充边节点信息
           new_arc->tailvex = p1;
           new_arc->headvex = p2;
   
           // 将边节点插入到弧尾顶点的出边链表头部
           new_arc->tlink = G->xlist[p1].firstout;
           G->xlist[p1].firstout = new_arc;
   
           // 将边节点插入到弧头顶点的入边链表头部
           new_arc->hlink = G->xlist[p2].firstin;
           G->xlist[p2].firstin = new_arc;
       }
   }
   

3. 打印图的函数

   这个函数可以帮助直观地看到生成的十字链表结构，包括每个顶点的出边和入边。

   // 打印十字链表
   void PrintOLGraph(OLGraph G) {
       int i;
       printf("\n十字链表如下：\n");
       for (i = 0; i < G.vexnum; ++i) {
           // 打印顶点信息
           printf("顶点 %c:\n", G.xlist[i].data);
   
           // 打印出边链表
           printf("  出边 -> ");
           ArcNode *p_out = G.xlist[i].firstout;
           while (p_out) {
               printf("%c ", G.xlist[p_out->headvex].data);
               p_out = p_out->tlink;
           }
           printf("\n");
   
           // 打印入边链表
           printf("  入边 <- ");
           ArcNode *p_in = G.xlist[i].firstin;
           while (p_in) {
               printf("%c ", G.xlist[p_in->tailvex].data);
               p_in = p_in->hlink;
           }
           printf("\n\n");
       }
   }
   

4. 主函数和完整代码

   将所有部分组合起来，可以创建一个完整的程序来演示十字链表的实现。

   #include <stdio.h>
   #include <stdlib.h>
   
   #define MAX_VERTEX_NUM 20
   typedef char VertexType;
   
   // 边表节点
   typedef struct ArcNode {
       int tailvex, headvex;
       struct ArcNode *hlink;
       struct ArcNode *tlink;
   } ArcNode;
   
   // 顶点表节点
   typedef struct VexNode {
       VertexType data;
       ArcNode *firstin, *firstout;
   } VexNode;
   
   // 图的结构体
   typedef struct {
       VexNode xlist[MAX_VERTEX_NUM];
       int vexnum, arcnum;
   } OLGraph;
   
   // 创建图的函数 (同上)
   void CreateOLGraph(OLGraph *G) {
       int i, k;
       printf("请输入有向图的顶点数和边数，用空格分隔：\n");
       scanf("%d %d", &G->vexnum, &G->arcnum);
   
       printf("请输入所有顶点的值：\n");
       for (i = 0; i < G->vexnum; ++i) {
           scanf(" %c", &G->xlist[i].data);
           G->xlist[i].firstin = NULL;
           G->xlist[i].firstout = NULL;
       }
   
       printf("请依次输入每条有向边的两个顶点（例如：v1 v2，表示从v1到v2）：\n");
       for (k = 0; k < G->arcnum; ++k) {
           char v1, v2;
           int p1 = -1, p2 = -1;
           scanf(" %c %c", &v1, &v2);
   
           for (i = 0; i < G->vexnum; ++i) {
               if (G->xlist[i].data == v1) p1 = i;
               if (G->xlist[i].data == v2) p2 = i;
           }
           if (p1 == -1 || p2 == -1) continue;
   
           ArcNode *new_arc = (ArcNode *)malloc(sizeof(ArcNode));
           if (new_arc == NULL) {
               printf("内存分配失败！\n");
               return;
           }
   
           new_arc->tailvex = p1;
           new_arc->headvex = p2;
   
           new_arc->tlink = G->xlist[p1].firstout;
           G->xlist[p1].firstout = new_arc;
   
           new_arc->hlink = G->xlist[p2].firstin;
           G->xlist[p2].firstin = new_arc;
       }
   }
   
   // 打印图的函数 (同上)
   void PrintOLGraph(OLGraph G) {
       int i;
       printf("\n十字链表如下：\n");
       for (i = 0; i < G.vexnum; ++i) {
           printf("顶点 %c:\n", G.xlist[i].data);
           printf("  出边 -> ");
           ArcNode *p_out = G.xlist[i].firstout;
           while (p_out) {
               printf("%c ", G.xlist[p_out->headvex].data);
               p_out = p_out->tlink;
           }
           printf("\n");
   
           printf("  入边 <- ");
           ArcNode *p_in = G.xlist[i].firstin;
           while (p_in) {
               printf("%c ", G.xlist[p_in->tailvex].data);
               p_in = p_in->hlink;
           }
           printf("\n\n");
       }
   }
   
   int main() {
       OLGraph G;
       CreateOLGraph(&G);
       PrintOLGraph(G);
       return 0;
   }
   

邻接多重表 (Adjacency Multilist)

邻接多重表（Adjacency Multilist）是针对无向图的另一种链式存储结构。它解决了邻接表在表示无向图时，每条边需要存储两次（在两个顶点的邻接链表中各存储一次）所带来的空间浪费问题。

其核心思想是：

• 每条边只对应一个边节点。
• 这个边节点同时被两个顶点的链表所共享。
• 边节点中除了存储两个相邻顶点的索引外，还包含指向这两个顶点各自下一条边的指针。

1. 图的结构定义

   需要定义 EdgeNode（边节点）和 VexNode（顶点节点）两种结构，以及表示图的 AMLGraph 结构。

   #include <stdio.h>
   #include <stdlib.h>
   
   #define MAX_VERTEX_NUM 20
   typedef char VertexType;
   
   // 边表节点 (EdgeNode)
   typedef struct EdgeNode {
       int mark; // 标记，用于遍历等操作
       int ivex, jvex; // 边所连接的两个顶点的索引
       struct EdgeNode *ilink; // 指向与顶点ivex相连的下一条边
       struct EdgeNode *jlink; // 指向与顶点jvex相连的下一条边
   } EdgeNode;
   
   // 顶点表节点 (VexNode)
   typedef struct VexNode {
       VertexType data; // 顶点信息
       EdgeNode *firstedge; // 指向与该顶点相连的第一条边
   } VexNode, AdjMultilist[MAX_VERTEX_NUM];
   
   // 图的结构体
   typedef struct {
       AdjMultilist vertices; // 邻接多重表
       int vexnum, edgenum; // 顶点数和边数
   } AMLGraph;
   

2. 创建图的函数

   这个函数会提示用户输入无向图的顶点和边的信息，并构建邻接多重表。

   // 创建一个无向图的邻接多重表
   void CreateAMLGraph(AMLGraph *G) {
       int i, k;
       printf("请输入无向图的顶点数和边数，用空格分隔：\n");
       scanf("%d %d", &G->vexnum, &G->edgenum);
   
       printf("请输入所有顶点的值：\n");
       for (i = 0; i < G->vexnum; ++i) {
           scanf(" %c", &G->vertices[i].data);
           G->vertices[i].firstedge = NULL; // 初始化边表头指针
       }
   
       printf("请依次输入每条边的两个顶点（例如：v1 v2）：\n");
       for (k = 0; k < G->edgenum; ++k) {
           char v1, v2;
           int p1 = -1, p2 = -1;
           scanf(" %c %c", &v1, &v2);
   
           // 查找顶点在数组中的索引
           for (i = 0; i < G->vexnum; ++i) {
               if (G->vertices[i].data == v1) p1 = i;
               if (G->vertices[i].data == v2) p2 = i;
           }
           if (p1 == -1 || p2 == -1) continue;
   
           // 创建新的边节点
           EdgeNode *new_edge = (EdgeNode *)malloc(sizeof(EdgeNode));
           if (new_edge == NULL) {
               printf("内存分配失败！\n");
               return;
           }
           
           // 填充边节点信息
           new_edge->mark = 0;
           new_edge->ivex = p1;
           new_edge->jvex = p2;
   
           // 将边节点插入到第一个顶点的边链表头部
           new_edge->ilink = G->vertices[p1].firstedge;
           G->vertices[p1].firstedge = new_edge;
   
           // 将边节点插入到第二个顶点的边链表头部
           new_edge->jlink = G->vertices[p2].firstedge;
           G->vertices[p2].firstedge = new_edge;
       }
   }
   

3. 打印图的函数

   这个函数可以帮助看到生成的邻接多重表结构，直观地展示每个顶点的边链表。

   // 打印邻接多重表
   void PrintAMLGraph(AMLGraph G) {
       int i;
       printf("\n邻接多重表如下：\n");
       for (i = 0; i < G.vexnum; ++i) {
           printf("顶点 %c: ", G.vertices[i].data);
           EdgeNode *p = G.vertices[i].firstedge;
           while (p) {
               // 判断当前节点是作为ivex还是jvex挂在链表上
               if (p->ivex == i) {
                   printf("->(%c, %c) ", G.vertices[p->ivex].data, G.vertices[p->jvex].data);
                   p = p->ilink;
               } else {
                   printf("->(%c, %c) ", G.vertices[p->jvex].data, G.vertices[p->ivex].data);
                   p = p->jlink;
               }
           }
           printf("\n");
       }
   }
   

4. 主函数和完整代码

   将所有部分组合起来，可以创建一个完整的程序来演示邻接多重表的实现。

   #include <stdio.h>
   #include <stdlib.h>
   
   #define MAX_VERTEX_NUM 20
   typedef char VertexType;
   
   // 边表节点
   typedef struct EdgeNode {
       int mark;
       int ivex, jvex;
       struct EdgeNode *ilink;
       struct EdgeNode *jlink;
   } EdgeNode;
   
   // 顶点表节点
   typedef struct VexNode {
       VertexType data;
       EdgeNode *firstedge;
   } VexNode, AdjMultilist[MAX_VERTEX_NUM];
   
   // 图的结构体
   typedef struct {
       AdjMultilist vertices;
       int vexnum, edgenum;
   } AMLGraph;
   
   // 创建图的函数 (同上)
   void CreateAMLGraph(AMLGraph *G) {
       int i, k;
       printf("请输入无向图的顶点数和边数，用空格分隔：\n");
       scanf("%d %d", &G->vexnum, &G->edgenum);
   
       printf("请输入所有顶点的值：\n");
       for (i = 0; i < G->vexnum; ++i) {
           scanf(" %c", &G->vertices[i].data);
           G->vertices[i].firstedge = NULL;
       }
   
       printf("请依次输入每条边的两个顶点（例如：v1 v2）：\n");
       for (k = 0; k < G->edgenum; ++k) {
           char v1, v2;
           int p1 = -1, p2 = -1;
           scanf(" %c %c", &v1, &v2);
   
           for (i = 0; i < G->vexnum; ++i) {
               if (G->vertices[i].data == v1) p1 = i;
               if (G->vertices[i].data == v2) p2 = i;
           }
           if (p1 == -1 || p2 == -1) continue;
   
           EdgeNode *new_edge = (EdgeNode *)malloc(sizeof(EdgeNode));
           if (new_edge == NULL) {
               printf("内存分配失败！\n");
               return;
           }
   
           new_edge->mark = 0;
           new_edge->ivex = p1;
           new_edge->jvex = p2;
   
           new_edge->ilink = G->vertices[p1].firstedge;
           G->vertices[p1].firstedge = new_edge;
   
           new_edge->jlink = G->vertices[p2].firstedge;
           G->vertices[p2].firstedge = new_edge;
       }
   }
   
   // 打印图的函数 (同上)
   void PrintAMLGraph(AMLGraph G) {
       int i;
       printf("\n邻接多重表如下：\n");
       for (i = 0; i < G.vexnum; ++i) {
           printf("顶点 %c: ", G.vertices[i].data);
           EdgeNode *p = G.vertices[i].firstedge;
           while (p) {
               if (p->ivex == i) {
                   printf("->(%c, %c) ", G.vertices[p->ivex].data, G.vertices[p->jvex].data);
                   p = p->ilink;
               } else {
                   printf("->(%c, %c) ", G.vertices[p->jvex].data, G.vertices[p->ivex].data);
                   p = p->jlink;
               }
           }
           printf("\n");
       }
   }
   
   int main() {
       AMLGraph G;
       CreateAMLGraph(&G);
       PrintAMLGraph(G);
       return 0;
   }
   

图的遍历

遍历是指从图中某个顶点出发，访问图中所有顶点且每个顶点仅被访问一次.

深度优先搜索 (DFS):

• 类似于树的先根遍历.
• 实现: 通常使用递归实现，并利用一个辅助数组 visited 来防止重复访问.
• 时间复杂度: 邻接矩阵为O(n²)，邻接表为O(n+e).

广度优先搜索 (BFS):

• 类似于树的层次遍历.
• 实现: 使用队列来管理需要访问的顶点，以实现按路径长度递增的逐层访问.
• 时间复杂度: 与DFS相同，邻接矩阵为O(n²)，邻接表为O(n+e).