LeetCode 1537.最大得分

你有两个 有序 且数组内元素互不相同的数组 nums1 和 nums2 。

一条 合法路径 定义如下：

选择数组 nums1 或者 nums2 开始遍历（从下标 0 处开始）。
从左到右遍历当前数组。
如果你遇到了 nums1 和 nums2 中都存在的值，那么你可以切换路径到另一个数组对应数字处继续遍历（但在合法路径中重复数字只会被统计一次）。
得分 定义为合法路径中不同数字的和。

请你返回 所有可能 合法路径 中的最大得分。由于答案可能很大，请你将它对 10^9 + 7 取余后返回。

示例 1：

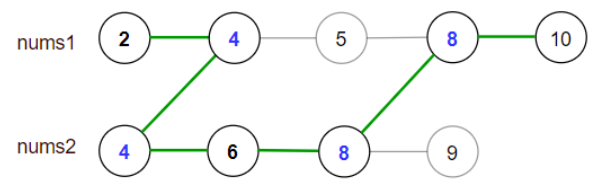
输入：nums1 = [2,4,5,8,10], nums2 = [4,6,8,9]
输出：30
解释：合法路径包括：
[2,4,5,8,10], [2,4,5,8,9], [2,4,6,8,9], [2,4,6,8,10],（从 nums1 开始遍历）
[4,6,8,9], [4,5,8,10], [4,5,8,9], [4,6,8,10] （从 nums2 开始遍历）
最大得分为上图中的绿色路径 [2,4,6,8,10] 。
示例 2：

输入：nums1 = [1,3,5,7,9], nums2 = [3,5,100]
输出：109
解释：最大得分由路径 [1,3,5,100] 得到。
示例 3：

输入：nums1 = [1,2,3,4,5], nums2 = [6,7,8,9,10]
输出：40
解释：nums1 和 nums2 之间无相同数字。
最大得分由路径[6,7,8,9,10]得到。

提示：

1 <= nums1.length, nums2.length <= 10${}^5$
1 <= nums1[i], nums2[i] <= 10${}^7$
nums1 和 nums2 都是严格递增的数组。

双序列双指针，找两个数组中相同值的节点，并计算到相同值的两条路径的得分，取较大者贪心即可：

class Solution {
public:
    int maxSum(vector<int>& nums1, vector<int>& nums2) {
        int idx1 = 0;
        int idx2 = 0;

        long long path1 = 0;
        long long path2 = 0;

        long long ans = 0;

        while (idx1 < nums1.size() && idx2 < nums2.size()) {
            // 移动两者中较小的那个，以找到相同值
            if (nums1[idx1] < nums2[idx2]) {
                path1 += nums1[idx1];
                ++idx1;
            } else if (nums1[idx1] > nums2[idx2]) {
                path2 += nums2[idx2];
                ++idx2;
            } else {
                // 找到相同值后，取较大得分的路径
                ans += max(path1, path2) + nums1[idx1];

                // 初始化下一段路径的得分
                path1 = 0;
                path2 = 0;

                ++idx1;
                ++idx2;
            }
        }

        while (idx1 < nums1.size()) {
            path1 += nums1[idx1];
            ++idx1;
        }

        while (idx2 < nums2.size()) {
            path2 += nums2[idx2];
            ++idx2;
        }

        ans += max(path1, path2);

        return ans % (long long)(1e9 + 7);
    }
};

如果nums1的长度为n，nums2的长度为m，则此算法时间复杂度为O(n+m)，空间复杂度为O(1)。