题目
请根据二叉树的前序遍历,中序遍历恢复二叉树,并打印出二叉树的右视图
数据范围: 0≤n≤100000≤n≤10000
要求: 空间复杂度 O(n)O(n),时间复杂度 O(n)O(n)
如输入[1,2,4,5,3],[4,2,5,1,3]时,通过前序遍历的结果[1,2,4,5,3]和中序遍历的结果[4,2,5,1,3]可重建出以下二叉树: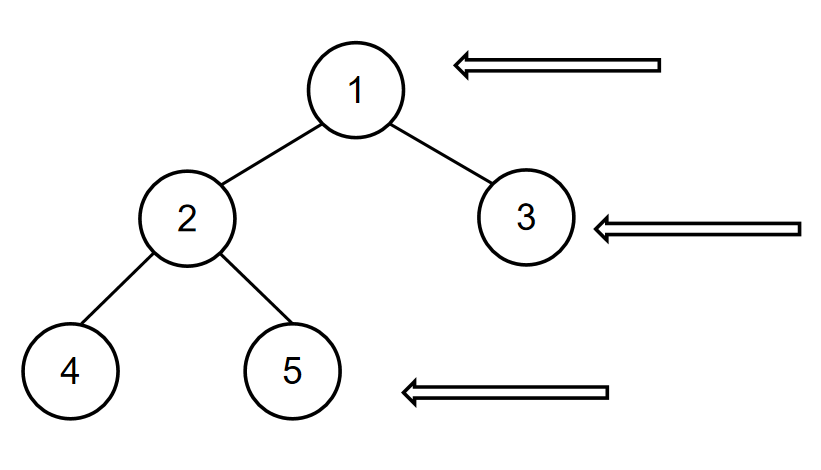
C++代码实现:
TreeNode* buildTree(vector<int> & xianxu, int l1, int r1, vector<int> &zhongxu, int l2, int r2)
{
if (l1 > r1 || l2 > r2) return NULL;
TreeNode* root = new TreeNode(xianxu[l1]);
int rootIndex = 0;
for (int i = l2; i <= r2; ++i)
{
if (zhongxu[i] == xianxu[l1])
{
rootIndex = i;
break;
}
}
int leftsize = rootIndex - l2;
int rightsize = r2 - rootIndex;
root->left = buildTree(xianxu, l1+1, l1+leftsize, zhongxu, l2, l2+leftsize-1);
root->right = buildTree(xianxu, l1+leftsize+1, r1, zhongxu, rootIndex+1, r2);
return root;
}
vector<int> rightSideView(TreeNode *root)
{
unordered_map<int, int> mp;
int max_depth = -1;
stack<TreeNode*> nodes;
stack<int> depth;
nodes.push(root);
depth.push(0);
while (!nodes.empty()){
TreeNode* node = nodes.top();
nodes.pop();
int depth1 = depth.top();
depth.pop();
if (node != NULL)
{
max_depth = max(depth1, max_depth);
if (mp.find(depth1) == mp.end())
{
mp[depth1] = node->val;
}
nodes.push(node->left);
nodes.push(node->right);
depth.push(depth1+1);
depth.push(depth1+1);
}
}
vector<int> res;
for (int i = 0; i <= max_depth; ++i)
{
res.push_back(mp[i]);
}
return res;
}
vector<int> solve(vector<int>& preOrder, vector<int>& inOrder) {
vector<int> res;
if (preOrder.size() == 0) return res;
TreeNode* root = buildTree(preOrder, 0, preOrder.size()-1, inOrder, 0, inOrder.size()-1);
return rightSideView(root);
}右视图是啥?
右视图就是「站在二叉树右边看过去,能看到的每个层的最右边节点」。比如下面这个树:
1 (第0层,看到1)
/ \
2 3 (第1层,看到3)
/ / \
4 5 6 (第2层,看到6)
右视图结果就是 [1,3,6]—— 核心是要拿到「每一层的第一个遇到的最右节点」。
为什么用栈?栈在这里的作用
栈是 “先进后出” 的容器,适合深度优先遍历(先往深了走,走到头再回头)。这里用了 两个栈:
nodes栈:存要遍历的二叉树节点;depth栈:存对应节点的 “深度”(根节点深度是 0,子节点比父节点深 1)。
两个栈是 “同步操作” 的 —— 弹出一个节点,就对应弹出它的深度;压入节点时,也对应压入它的深度。
逐行拆解代码逻辑(结合例子看更清楚)
咱们就用上面的树 [1,2,3,4,5,6] 当例子,一步一步看栈和数据的变化。
初始状态
一开始,把根节点 1 和它的深度 0 分别压入两个栈:
nodes栈:[1](栈顶是 1)depth栈:[0](栈顶是 0)mp(存 “深度→最右节点值”):空max_depth(记录最大深度):-1
进入循环:while (!nodes.empty ())(栈不空就继续)
循环的核心逻辑是:弹出栈顶节点→判断是不是有效节点→处理有效节点→压入它的子节点。
第一步:弹出节点和对应深度
TreeNode* node = nodes.top(); // 取nodes栈顶节点(一开始是1)
nodes.pop(); // 把1从nodes栈弹出,nodes现在空了
int depth1 = depth.top(); // 取depth栈顶深度(0)
depth.pop(); // 把0从depth栈弹出,depth现在空了
此时:node=1,depth1=0。
第二步:判断节点是否有效(非 NULL)
if (node != NULL) // 1不是NULL,进入处理
{
// 1. 更新最大深度:当前深度0比初始的-1大,所以max_depth=0
max_depth = max(depth1, max_depth); // max(0,-1)=0
// 2. 记录当前深度的最右节点(关键!)
if (mp.find(depth1) == mp.end()) // 查mp里有没有深度0的记录?一开始没有
{
mp[depth1] = node->val; // 把深度0和值1存进去,mp现在是 {0:1}
}
// 3. 压入当前节点的左、右子节点(重点!栈是先进后出,所以先压左,再压右)
nodes.push(node->left); // 压入1的左子节点2 → nodes栈:[2]
nodes.push(node->right); // 再压入1的右子节点3 → nodes栈:[2,3](栈顶是3)
// 4. 同步压入子节点的深度(父节点深度+1=0+1=1)
depth.push(depth1+1); // 压入2的深度1 → depth栈:[1]
depth.push(depth1+1); // 再压入3的深度1 → depth栈:[1,1](栈顶是1)
}
这一步结束后
nodes栈:[2,3](栈顶是 3)depth栈:[1,1](栈顶是 1)mp:{0:1}max_depth:0
第三步:继续循环(nodes 栈不空,处理栈顶的 3)
重复第一步:弹出节点和深度
node = nodes.top()→ 3;nodes.pop()→ nodes 变成 [2]depth1 = depth.top()→ 1;depth.pop()→ depth 变成 [1]
判断 3 非 NULL,进入处理:
- 更新 max_depth:max (1,0)=1 → max_depth=1;
- 查 mp 有没有深度 1 的记录?没有 → mp [1]=3 → mp 现在 {0:1, 1:3};
- 压入 3 的左、右子节点:
- 3 的左是 5,右是 6 → 先压左(5),再压右(6)→ nodes 栈变成 [2,5,6](栈顶是 6);
- 同步压入深度 1+1=2 → depth 栈变成 [1,2,2](栈顶是 2)。
这一步结束后:
nodes栈:[2,5,6]depth栈:[1,2,2]mp:{0:1, 1:3}max_depth:1
第四步:继续循环(处理栈顶的 6)
弹出 6 和深度 2:
node=6,depth1=2(非 NULL);
- 更新 max_depth:max (2,1)=2 → max_depth=2;
- 查 mp 有没有深度 2 的记录?没有 → mp [2]=6 → mp 现在 {0:1,1:3,2:6};
- 压入 6 的左、右子节点(都是 NULL)→ nodes 栈变成 [2,5,NULL,NULL];
- 同步压入深度 3 → depth 栈变成 [1,2,3,3]。
这一步后,mp 已经存好了所有层的最右节点,后续再处理 NULL 节点和剩下的 2、5,都不会修改 mp 了(因为 mp 里对应深度已有值)。
后续循环:处理 NULL 和剩余节点
比如处理 6 的左子节点(NULL):弹出后判断是 NULL,直接跳过,不做任何处理;
处理 5 时,深度是 2,但 mp 里已有深度 2 的记录(6),所以不会覆盖;
处理 2 时,深度是 1,mp 里已有深度 1 的记录(3),也不会覆盖。
直到栈空,循环结束。
最后:生成结果
vector<int> res;
for (int i = 0; i <= max_depth; ++i) // 从深度0到2,依次取mp的值
{
res.push_back(mp[i]); // 0→1,1→3,2→6 → res=[1,3,6]
}
return res;
关键:为什么先压左子节点,再压右子节点?
这是保证拿到「最右节点」的核心
因为栈是 “先进后出”:先压左,再压右 → 下一次弹出时,会先弹右子节点。
比如节点 1 的子节点:先压 2,再压 3 → 下次先弹 3(右节点),这样 3 就会被优先处理,成为深度 1 的最右节点;
节点 3 的子节点:先压 5,再压 6 → 下次先弹 6(右节点),成为深度 2 的最右节点。
如果反过来先压右再压左,就会先处理左节点,拿到的就是「左视图」了
总结:这段代码的逻辑一句话说
用两个栈同步存节点和深度,通过 “先压左、再压右” 保证每次先处理层的右节点,用哈希表记录每一层第一个遇到的右节点(就是最右节点),最后按深度顺序收集结果,就是右视图。