LeetCode刷题-top100（ 矩阵置零）

73. 矩阵置零

给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法。

示例 1：

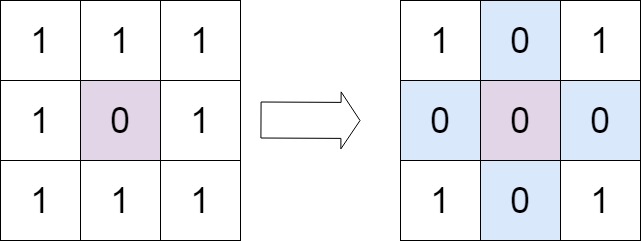
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

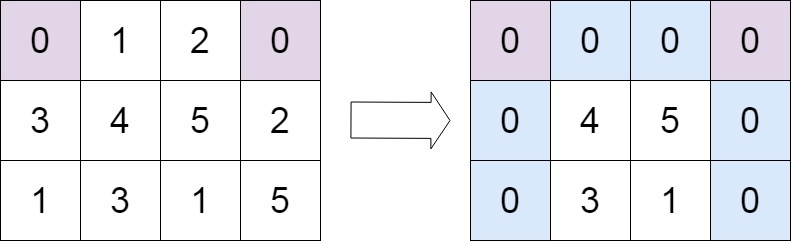
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

代码：使用标记数组（空间复杂度 O(m+n)）

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        
        boolean[] rowZero = new boolean[m];
        boolean[] colZero = new boolean[n];
        
        // 第一次遍历：标记哪些行和列需要置零
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == 0) {
                    rowZero[i] = true;
                    colZero[j] = true;
                }
            }
        }
        
        // 第二次遍历：根据标记置零
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (rowZero[i] || colZero[j]) {
                    matrix[i][j] = 0;
                }
            }
        }
    }
}

最优解：原地算法（空间复杂度 O(1)）

class Solution {
    public void setZeroes(int[][] matrix) {
        int m = matrix.length;
        int n = matrix[0].length;
        
        boolean firstRowZero = false;
        boolean firstColZero = false;
        
        // 检查第一行是否有0
        for (int j = 0; j < n; j++) {
            if (matrix[0][j] == 0) {
                firstRowZero = true;
                break;
            }
        }
        
        // 检查第一列是否有0
        for (int i = 0; i < m; i++) {
            if (matrix[i][0] == 0) {
                firstColZero = true;
                break;
            }
        }
        
        // 使用第一行和第一列作为标记
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][j] == 0) {
                    matrix[i][0] = 0;
                    matrix[0][j] = 0;
                }
            }
        }
        
        // 根据标记置零
        for (int i = 1; i < m; i++) {
            for (int j = 1; j < n; j++) {
                if (matrix[i][0] == 0 || matrix[0][j] == 0) {
                    matrix[i][j] = 0;
                }
            }
        }
        
        // 处理第一行
        if (firstRowZero) {
            for (int j = 0; j < n; j++) {
                matrix[0][j] = 0;
            }
        }
        
        // 处理第一列
        if (firstColZero) {
            for (int i = 0; i < m; i++) {
                matrix[i][0] = 0;
            }
        }
    }
}