线性代数 · 行列式 | Sarrus Rules / Laplace Expansion

注：本文为 “线性代数 · 行列式展开” 相关合辑。
图片清晰度受引文原图所限。
略作重排，未全校去重。
部分段落有编订，如有内容异常，请看原文。

萨鲁斯法则

百科

一、基本定义

萨鲁斯法则（Sarrus Rule）是展开二阶和三阶行列式的方法，其核心表述为：二阶和三阶行列式的值等于主对角线上元素的乘积减去次对角线上元素的乘积，因此该法则也被称为对角线法则。

在 $n$ 阶行列式 $D=|a_{ij}|$ 中：

• 从左上角到右下角的连线称为行列式 $D$ 的主对角线，线上的元素 $a_{11},a_{22},\dots ,a_{nn}$ 称为主对角元；
• 从右上角到左下角的连线称为行列式 $D$ 的次对角线，线上的元素 $a_{1n},a_{2,n-1},\dots ,a_{n1}$ 称为次对角元。

需特别注意：仅二阶和三阶行列式适用萨鲁斯法则，四阶及以上行列式不存在萨鲁斯法则。

二、展开方法

二阶和三阶行列式按萨鲁斯法则展开的核心逻辑为：实线上元素的乘积带正号，虚线上元素的乘积带负号，将所有这些乘积相加，即可得到行列式的展开式（对应图示：图 1 二阶行列式按萨鲁斯法则展开、图 2 三阶行列式按萨鲁斯法则展开）。

（一）二阶行列式展开

设二阶行列式为：
$$\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|$$
根据萨鲁斯法则，其展开式为：
$$\left|\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right|=a_{11}{a}_{22}-a_{12}{a}_{21}$$

（二）三阶行列式展开

设三阶行列式为：
$$\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|$$
根据萨鲁斯法则，其展开式为：
$$\left|\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right|=a_{11}{a}_{22}{a}_{33}+a_{12}{a}_{23}{a}_{31}+a_{13}{a}_{21}{a}_{32}-a_{13}{a}_{22}{a}_{31}-a_{12}{a}_{21}{a}_{33}-a_{11}{a}_{23}{a}_{32}$$

三、例题解析

【例 1】行列式化简（已知 $a+b+c=0$）

已知 $a+b+c=0$，求行列式 $\left|\begin{array}{ccc}a& b& c\\ b& c& a\\ c& a& b\end{array}\right|$ 的值。

提示：按萨鲁斯法则展开，再结合 $a+b+c=0$ 分解因式。

解：答案为 $0$，具体推导如下：

1. 按萨鲁斯法则展开行列式：
   $$\left|\begin{array}{ccc}a& b& c\\ b& c& a\\ c& a& b\end{array}\right|=acb+bac+cba-c^3-a^3-b^3$$
2. 合并同类项并整理：
   $$\text{展开式}=3abc-a^3-b^3-c^3$$
3. 结合已知条件 $a+b+c=0$，得 $c=-a-b$，代入上式：
   $$\begin{array}{rl}3abc-a^3-b^3-c^3& =3ab(-a-b)-a^3-b^3-(-a-b{)}^3\\ & =-3a^{2}b-3a{b}^2-a^3-b^3+(a^3+b^3+3a^{2}b+3a{b}^2)\\ & =0\end{array}$$

【例 2】求行列式展开式中指定项的系数

求行列式 $\left|\begin{array}{ccc}-1& 1& 1\\ 1& -1& x\\ 1& 1& -1\end{array}\right|$ 的展开式中 $x$ 的系数。

提示：不必全部展开，从萨鲁斯法则分析含 $x$ 的项即可。

解：答案为 $2$，具体分析如下：
根据萨鲁斯法则，行列式展开式中含 $x$ 的项仅由“实线上含 $x$ 的乘积项”和“虚线上含 $x$ 的乘积项”构成：

1. 实线上含 $x$ 的项：$1\cdot x\cdot 1$，带正号，即 $+x$；
2. 虚线上含 $x$ 的项：$(-1)\cdot x\cdot 1$，带负号，即 $-(-1\cdot x\cdot 1)=+x$；
3. 合并含 $x$ 的项：$x+x=2x$，因此 $x$ 的系数为 $2$。

四、参考资料

[1] 《数学辞海》编辑委员会．数学辞海·第一卷．中国科学技术出版社，2002：第 425 页
[2] 袁中阳，张云霞主编．线性代数．南京大学出版社，2015.08：第 4 页
[3] 肖楚阳主编．经济应用数学基础（二）线性代数（人大·第 4 版）同步辅导及习题全解．中国水利水电出版社，2016.03：第 4 页

知乎讨论：为什么萨吕法则（Rule of Sarrus）不适用于 $4\times 4$ 或更大的行列式？

匿名用户 _zhihu

在行列式计算中，萨吕法则（Rule of Sarrus）是一种用于计算 $2\times 2$ 和 $3\times 3$ 行列式的简便方法。然而，该法则并不适用于 $4\times 4$ 或更大的行列式。

下文将详细解释其原因。

萨吕法则与莱布尼茨行列式公式

萨吕法则是莱布尼茨行列式公式（Leibniz Determinants Formula）的特例。莱布尼茨行列式公式如下：

莱布尼茨行列式公式：

设 $\sigma$ 是一个置换，$S_n$ 是 1 到 $n$ 上的全体置换，则行列式可定义为：

$$\det (A)=\sum _{\sigma \in S_n}\mathrm{sgn}(\sigma )\prod _{i=1}^n{a}_{i,\sigma (i)}$$

对于 $2\times 2$ 行列式，仅有两个置换；对于 $3\times 3$ 行列式，有六个置换。这些置换的逆序数各占一半，因此恰好可以表示为左斜减右斜的形式。

然而，对于 $4\times 4$ 行列式，有 $4!=24$ 个置换，而萨吕法则仅能涵盖其中的 8 个，显然无法完整表示。例如：

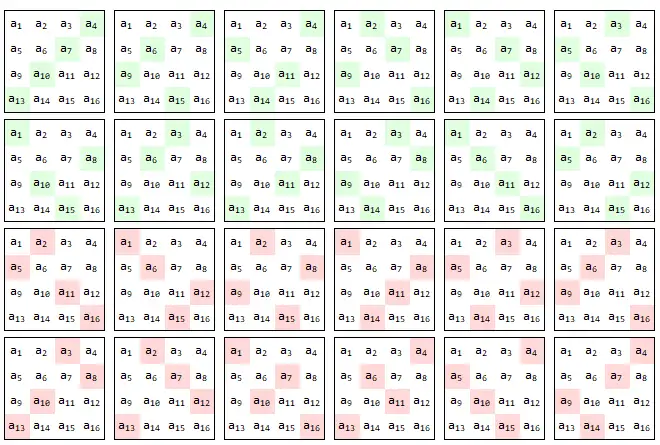
其中，绿色表示取正，红色表示取负。随着置换数量的增加，其复杂性也显著提高，已不再是简单的全斜形式。

四阶行列式的尝试与局限

尽管有人尝试推广萨吕法则以适用于四阶行列式，但这些尝试均未能成功。

例如，尝试通过两次线性列变换，重排得到另外两个行列式，从而补齐了 24 种置换。

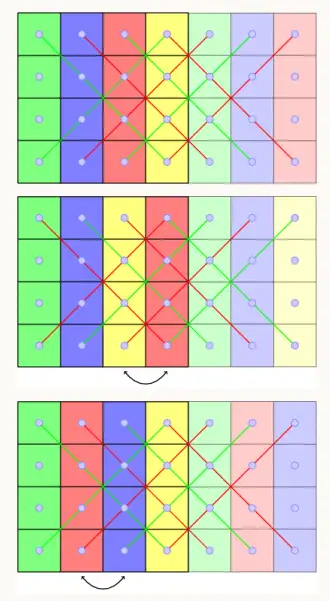
然而，这种方法对于五阶行列式（有 120 种置换）已无法简单地通过列变换全部实现，且复杂性极高，难以通过手工计算完成。

相关尝试可参考以下链接：

• Sarrus Rules for 4 x 4 | regularize
• Sarrus Rules for 4 x 4 (second try) | regularize

计算复杂性

随着行列式阶数的增加，行列式的计算复杂性呈指数增长。对于 $n\times n$ 行列式，其行列式的计算涉及 $n!$ 个置换，每个置换对应一个乘积项。这种复杂性使得萨吕法则无法扩展到 $4\times 4$ 或更大的行列式。因此，对于高阶行列式计算，通常需要借助更高效的算法或计算工具。

有兴趣者可自行运行代码查看结果：

rule[co_] := If[First@co === -1,
    (# -> Item[#, Background -> LightRed]) & /@ co,
    (# -> Item[#, Background -> LightGreen]) & /@ co
];
m = Table[Subscript[a, i + j], {i, 0, 5^2 - 1, 5}, {j, 1, 5, 1}];
pt = Sort[MonomialList[m // Det], First] /. {Times -> List};
g = Grid[m /. rule[#], Frame -> True, Spacings -> {0.5, 1}] & /@ pt;
Grid@Partition[g, 12]

结论

萨吕法则仅适用于 $2\times 2$ 和 $3\times 3$ 行列式，而不适用于 $4\times 4$ 或更大的行列式。这是由于高阶行列式计算涉及更多的置换和乘积项，其复杂性远超萨吕法则所能涵盖的范围。因此，在处理高阶行列式时，应采用更通用的莱布尼茨行列式公式或其他高效的计算方法。

发布于 2018-07-13 17:29

u753b 回答

确实是，…超过 3X3 的行列式计算上是会出错的，助教老师举了一个例子。

发布于 2018-05-24 04:46

拉普拉斯展开（Laplace Expansion）

行列式的拉普拉斯展开（Laplace Expansion），也称为代数余子式展开（Cofactor Expansion），是计算行列式的一种核心方法，适用于各类方阵（包括高阶方阵）的行列式计算。

一、方法原理

对于 $n$ 阶行列式 $D=\det (a_{ij})$，选择某一行（或某一列），则行列式的值等于该行（或该列）所有元素与其对应的**代数余子式（Cofactor）**乘积的和。即：

若按第 $i$ 行展开，有

$$D=a_{i1}{A}_{i1}+a_{i2}{A}_{i2}+\cdots +a_{in}{A}_{in}(i=1,2,\cdots ,n)$$

若按第 $j$ 列展开，有

$$D=a_{1j}{A}_{1j}+a_{2j}{A}_{2j}+\cdots +a_{nj}{A}_{nj}(j=1,2,\cdots ,n)$$

其中，$A_{ij}=(-1{)}^{i+j}{M}_{ij}$ 称为元素 $a_{ij}$ 的代数余子式，$M_{ij}$ 是划去 $a_{ij}$ 所在的第 $i$ 行和第 $j$ 列后，剩余元素构成的 $(n-1)$ 阶行列式，称为余子式（Minor）。

二、计算步骤（以按第一行展开为例，结合图中示例）

考虑行列式

$$D=\left|\begin{array}{cccc}1& 5& 7& 2\\ 2& 1& 5& 1\\ 5& 3& 4& 8\\ 7& 3& 3& 6\end{array}\right|$$

按第一行展开计算其值，步骤如下：

1. 取第一行第 1 列元素 $a_{11}=1$：
   • 划去第 1 行、第 1 列，得到余子式 $M_{11}=\left|\begin{array}{ccc}1& 5& 1\\ 3& 4& 8\\ 3& 3& 6\end{array}\right|$；
   • 计算代数余子式 $A_{11}=(-1{)}^{1+1}{M}_{11}=M_{11}$；
   • 该项为 $a_{11}{A}_{11}=1\cdot M_{11}$。
2. 取第一行第 2 列元素 $a_{12}=5$：
   • 划去第 1 行、第 2 列，得到余子式 $M_{12}=\left|\begin{array}{ccc}2& 5& 1\\ 5& 4& 8\\ 7& 3& 6\end{array}\right|$；
   • 计算代数余子式 $A_{12}=(-1{)}^{1+2}{M}_{12}=-M_{12}$；
   • 该项为 $a_{12}{A}_{12}=5\cdot (-M_{12})=-5\cdot M_{12}$。
3. 取第一行第 3 列元素 $a_{13}=7$：
   • 划去第 1 行、第 3 列，得到余子式 $M_{13}=\left|\begin{array}{ccc}2& 1& 1\\ 5& 3& 8\\ 7& 3& 6\end{array}\right|$；
   • 计算代数余子式 $A_{13}=(-1{)}^{1+3}{M}_{13}=M_{13}$；
   • 该项为 $a_{13}{A}_{13}=7\cdot M_{13}$。
4. 取第一行第 4 列元素 $a_{14}=2$：
   • 划去第 1 行、第 4 列，得到余子式 $M_{14}=\left|\begin{array}{ccc}2& 1& 5\\ 5& 3& 4\\ 7& 3& 3\end{array}\right|$；
   • 计算代数余子式 $A_{14}=(-1{)}^{1+4}{M}_{14}=-M_{14}$；
   • 该项为 $a_{14}{A}_{14}=2\cdot (-M_{14})=-2\cdot M_{14}$。

最终，行列式 $D$ 的值为上述四项之和，即

$$D=1\cdot M_{11}-5\cdot M_{12}+7\cdot M_{13}-2\cdot M_{14}$$

再分别计算各余子式的值并代入，可得 $D=-456$。

三、方法特点与意义

1. 避免重复与简化计算：计算每个元素的代数余子式时，仅关注该元素所在行、列之外的元素，剔除了冗余的行、列信息，减少了重复计算，使高阶行列式计算可逐步降阶为低阶行列式计算。
2. 通用性：适用于所有方阵的行列式计算，是线性代数中计算行列式的基础方法之一，在数学理论推导（如证明行列式性质）、工程技术（如求解线性方程组、分析矩阵特征）等领域广泛应用。

via：

• 萨鲁斯法则_百度百科
  https://baike.baidu.com/item/萨鲁斯法则/18881592

• 为什么萨吕法则（Rule of Sarrus）不适用于 $4\times 4$ 或是更大的行列式？ - 知乎
  https://www.zhihu.com/question/277330231

• Regel von Sarrus 3x3 Determinante berechnen - Simplexy
  https://www.simplexy.de/mathe-klasse-12/matrix/regel-von-sarrus.php

• How to find the Determinant of a 3x3 Matrix (practice problems)
  https://www.algebrapracticeproblems.com/how-to-find-the-determinant-of-a-3x3-matrix/

• Sarrus’s Rule: What It Consists of and Types of Determinants - science - 2025
  https://warbletoncouncil.org/regla-de-sarrus-3577