因果推断 | 从因果树到因果森林：理论解析与代码实践-EW帮帮网

文章目录

1 引言
2 因果树
3 因果森林
4 代码实例
5 总结
6 相关阅读

1 引言

上一篇文章发表日期是7月27日。考虑到我在8月休了半个月婚假，能在有限的空闲时间里抽空学习并沉淀自己的认知内容，已让我感到十分满足。

当然，能在9月中旬完成这篇文章，除了个人的“努力”之外，内容本身不算复杂也是一个重要原因。本篇文章的核心是“因果森林”。对于具备一定机器学习基础的读者而言，“因果森林”这一名称很容易让人联想到“随机森林”。事实上，两者之间确实存在诸多相似之处。将它们进行对比，有助于更深入地理解“因果森林”的算法原理。

正文如下。

2 因果树

正如学习随机森林之前需先掌握决策树，介绍因果森林前也需先理解因果树。

2.1 算法原理

因果树的概念提出于2016年，主要用于评估异质性因果效应（heterogeneous causal effects）。简单来说，如果某一处理（treatment）对所有样本的效果一致，则为同质性因果效应，例如接种疫苗后所有人感染概率均下降90%；而如果处理在不同子群体或特征下效果不同，则为异质性因果效应，例如广告在不同地区的转化率提升幅度不同。

一个简单的因果树结构如下：原始样本集 $S$ 的平均因果效应为 $\tau_S$ 。通过某种分割规则，形成左叶节点 $S_L$ 和右叶节点 $S_R$ ，对应的因果效应分别为 $\tau_L$ 和 $\tau_R$ 。

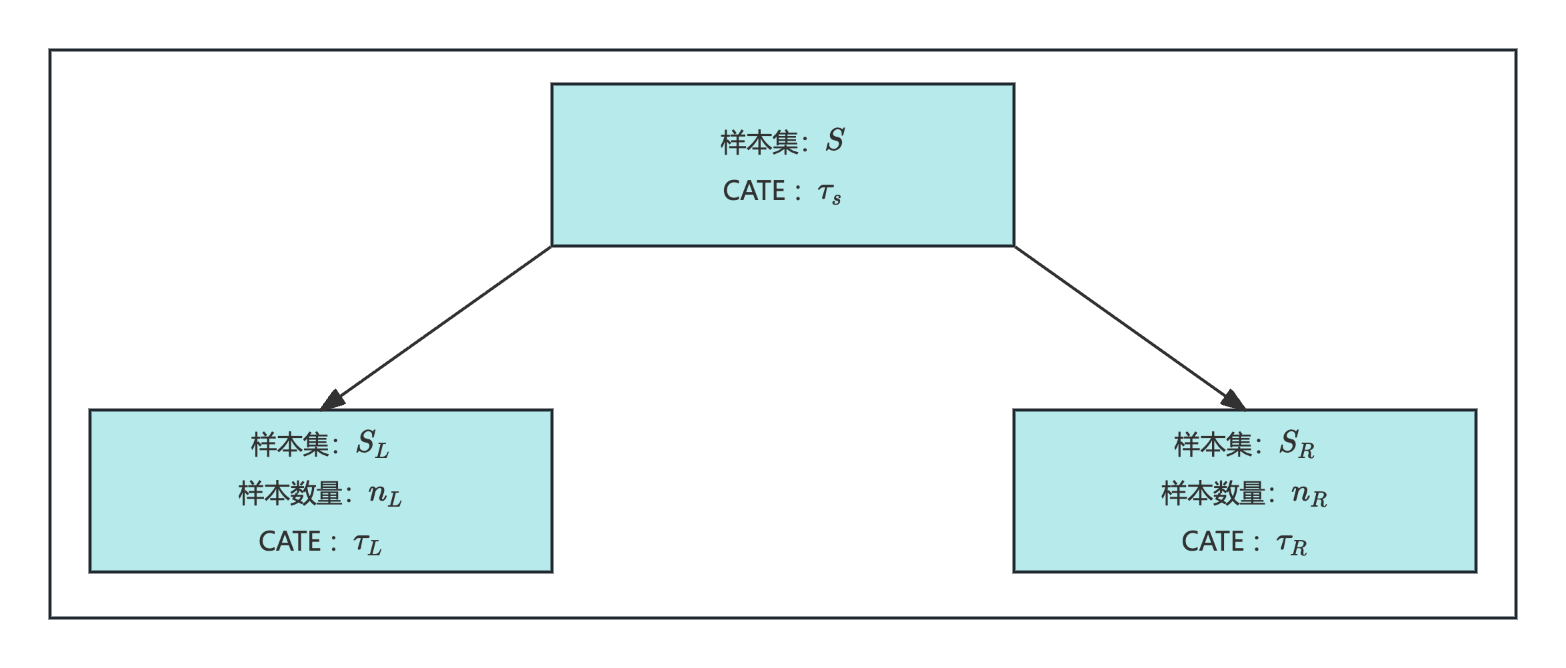
每个分组的CATE计算方式为：
$\tau = Y_1-Y_0$
其中， $Y_1$ 和 $Y_0$ 分别表示分组内处理组和对照组的平均结果值。

$S_L$ 和 $S_R$ 代表不同子群体， $\tau_L$ 和 $\tau_R$ 的差异越大，说明树的划分越有效。划分优劣可通过以下指标衡量：
$n_L ·(\tau_L-\tau_S)^2 + n_R ·(\tau_R-\tau_S)^2$
$Q$ 值越大，说明分割带来的处理效应差异越显著，分割更“有意义”。

算法原理如上，较为简明。下表对比了决策树（用于分类）与因果树：

	决策树	因果树
目标	分类	估计处理效应
分割标准	最小化不纯度gini	最大化 $Q$
叶节点内容	分类结果	CATE
适用场景	分类预测	异质性效应估计

在数据集划分方面，决策树和因果树也有所不同：

决策树：通常划分为训练集和测试集，训练集用于模型训练，测试集用于评估泛化能力。
因果树：通常划分为分割集和估计集，前者用于确定分割规则，后者用于计算CATE，这种方法称为“Honest approaches”。

2.2 实例计算

为加深对因果树算法的理解，下面通过具体实例手动演示划分过程。

假设有一份医疗实验数据集，包含以下信息：

特征：年龄（Age）、性别（Gender）
处理：是否服用新药（Treatment, 1=服用，0=未服用）
结果：血压下降值（Outcome, 单位mmHg）

我们希望利用因果树发现不同人群对新药的降压效果。数据共20条，明细如下：

ID	Age	Gender	Treatment	Outcome
1	22	0	1	13
2	33	1	0	7
3	41	0	1	10
4	27	1	0	6
5	38	0	1	12
6	45	1	1	9
7	36	0	0	8
8	24	1	0	7
9	52	0	1	8
10	29	1	0	6
11	31	0	1	11
12	40	1	0	8
13	23	0	1	14
14	47	1	0	5
15	34	0	0	6
16	51	1	1	7
17	26	0	0	7
18	39	1	1	10
19	44	0	0	5
20	28	1	1	12

2.2.1 划分原始数据集

首先，将原始数据随机分为分割集（前10条）和估计集（后10条）。

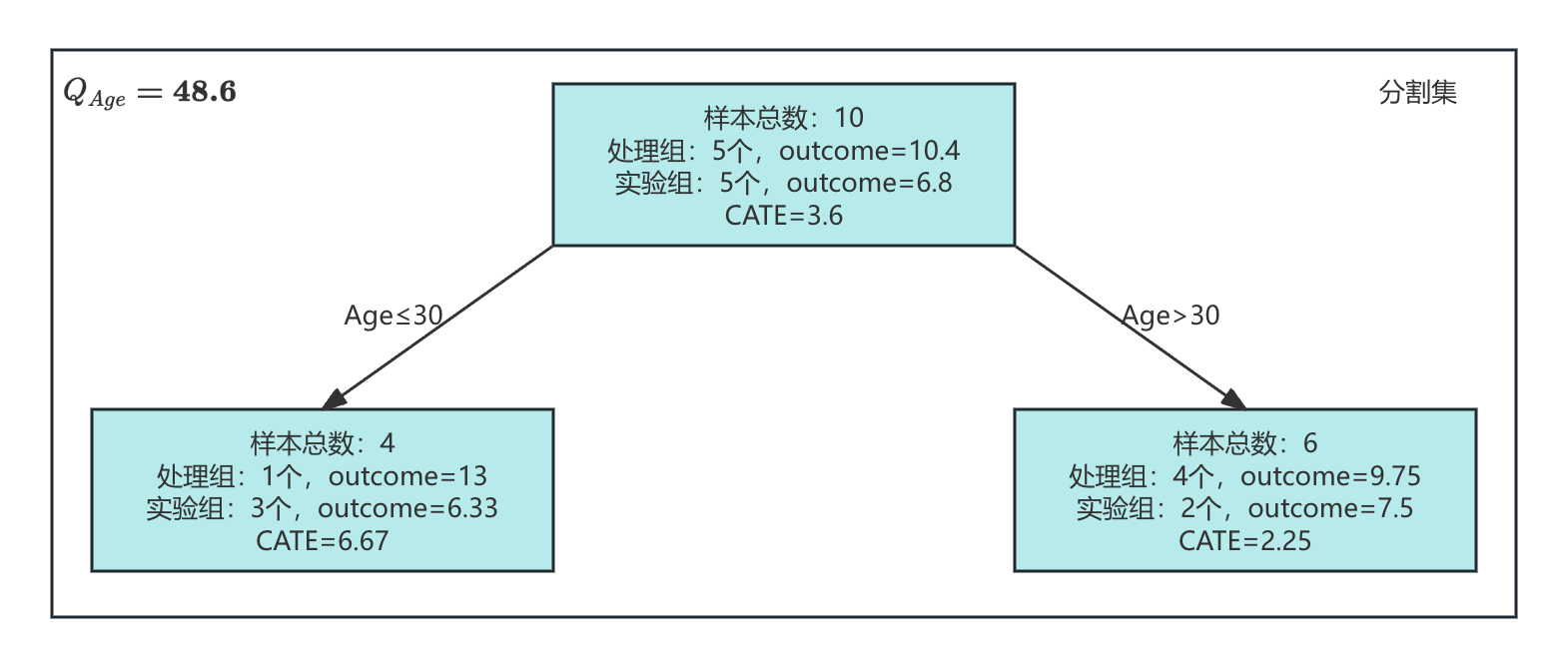
分割集中，处理组的ID为1,3,5,6,9，平均结果变量为10.4；对照组的ID为2,4,7,8,10，平均结果变量为6.8。因此，分割集总体CATE为：
$\tau_S=10.4 - 6.8 = 3.6$

2.2.2 确定最佳分割

假设允许两种分割方式：按Age=30划分，或按性别划分。

按Age=30划分：

左叶节点（Age≤30）：共4个样本。处理组的ID为1，结果变量为13；对照组的ID为4,8,10，平均结果变量为6.33。CATE为：
$\tau_L=13 - 6.33 = 6.67$
右叶节点（Age>30）：共6个样本。处理组的ID为3,5,6,9，平均结果变量为9.75；对照组的ID为2和7，平均结果变量为7.5。CATE为：
$\tau_R=9.75 - 7.5 = 2.25$

对应的 $Q$ 值为：
$Q_{age}=4·(6.67-3.6)^2 + 6·(2.25-3.6)^2=48.6$

如下图所示，分割集在Age=30条件下的分割结果：

**按性别分割：**同理计算，得到 $Q_{gender}=9.7$ 。

由于 $Q_{gender} < Q_{age}$ ，因此Age=30是更优的分割方案。

2.2.3 评估因果效应

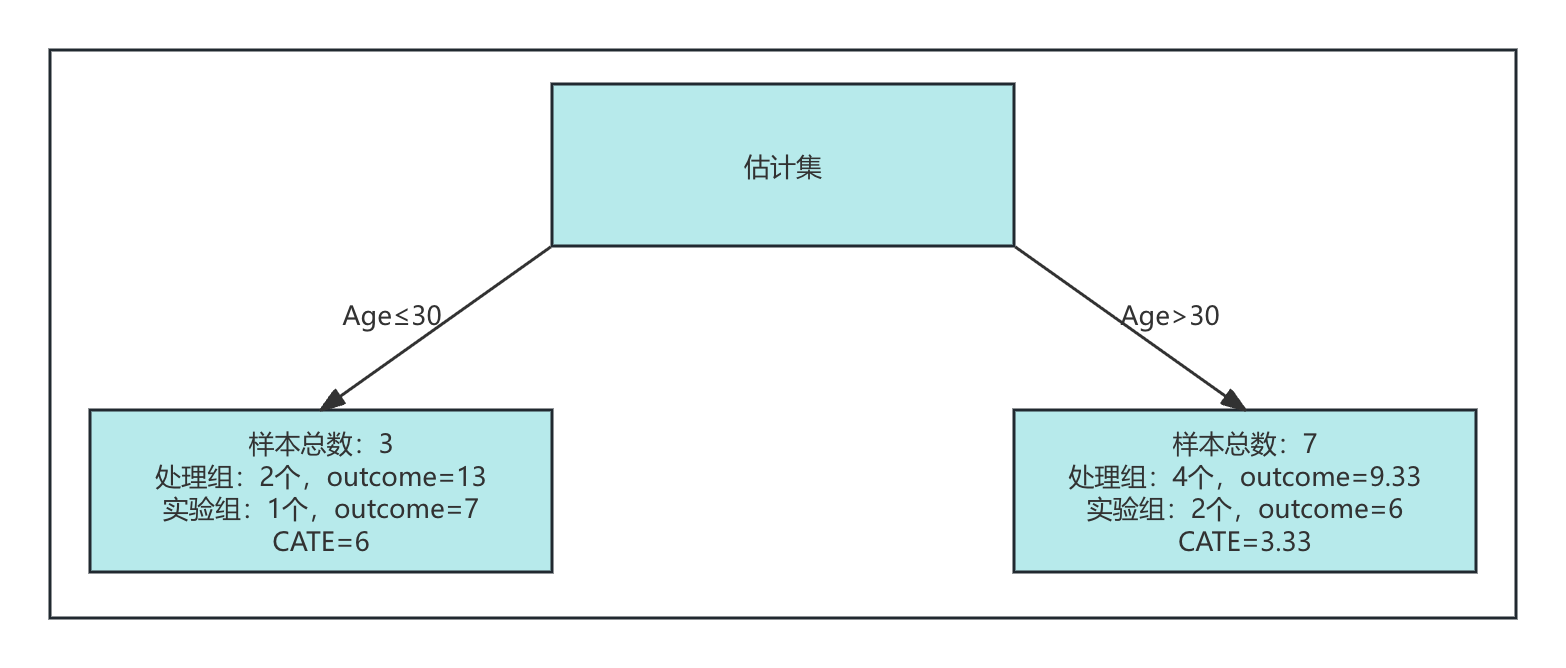
切换至估计集，按照Age=30标准分组：

左叶节点：共3个样本。处理组的ID为13和20，平均结果变量为13；对照组的ID为17，结果变量为7。CATE为13-7=6。
右叶节点：共7个样本。处理组的ID为11,16,18，平均结果变量为9.33；对照组的ID为12,14,15,19，平均结果变量为6。CATE为9.33 - 6 = 3.33。

最终评估结果如下：

分组	CATE
Age≤30	6
Age>30	3.33

估计集在Age=30条件下的分割结果如下图所示：

3 因果森林

因果森林可以理解为由多棵因果树组成的集成模型，其算法原理与随机森林高度相似，具体内容可参考：随机森林原理和性能分析。

多棵树优于单棵树的理论基础是孔多塞陪审团定理。简而言之，多数投票的正确概率高于任何单一模型；当模型数量足够大时，集成模型的准确率将趋近于完美。

基于因果树构建因果森林，常见的两种方式如下：

Bootstrap采样（Bagging）：每棵因果树都在从原始数据集有放回抽样得到的子集（bootstrap sample）上训练。这种方式可以降低单棵树对特定数据点的依赖，提高集成模型的稳健性。
特征随机选择（Random Feature Selection）：每次分裂节点时，并非使用全部特征，而是从中随机选择一部分作为候选分割变量。这可以避免某些强特征主导所有树的分割，提高模型对高维数据的适应能力，并减少过拟合。

训练完因果森林后，对每个样本的CATE估算方式是：在所有树中分别预测其CATE，然后对这些预测值取平均。

4 代码实例

下面展示如何通过代码使用因果森林模型估计因果效应。

整体代码框架与因果推断 | 元学习方法原理详解和代码实操一致，分为三个主要步骤：

构造实例数据：需要注意的是，树模型适用于评估异质性因果效应，因此将synthetic_data中的mode参数由1（线性结果）改为2（非线性结果）。
训练算法模型：使用causalml工具包，分别调用CausalTreeRegressor和CausalRandomForestRegressor以实现因果树和因果森林模型。为便于对比，代码中还保留了X-learner和DML模型。
评估模型效果：评估指标包括ATE、IDE和AUUC，并对IDE和AUUC进行了可视化展示。

import numpy as np
import pandas as pd
from xgboost import XGBRegressor
from causalml.inference.meta import BaseXRegressor
from causalml.dataset import synthetic_data
from econml.dml import CausalForestDML
from causalml.metrics import auuc_score, plot_gain
import matplotlib.pyplot as plt
from causalml.inference.tree import CausalRandomForestRegressor, CausalTreeRegressor


def plot_sorted_tau_and_preds(df):
    # tau真实值和4个模型预测
    tau = df['tau_true'].values
    preds = {
        'X-learner': df['x-learner'].values,
        'DML': df['DML'].values,
        'CausalForest': df['CausalForest'].values,
        'CausalTree': df['CausalTree'].values
    }
    # 排序索引
    idx = np.argsort(tau)
    tau_sorted = tau[idx]
    preds_sorted = {k: v[idx] for k, v in preds.items()}
    x = np.arange(len(tau))

    # 统一y轴范围
    y_all = [tau_sorted] + [preds_sorted[k] for k in preds]
    ymin = min([arr.min() for arr in y_all])
    ymax = max([arr.max() for arr in y_all])

    # 画4个子图
    fig, axes = plt.subplots(2, 2, figsize=(16, 12))
    model_names = list(preds.keys())
    for i, ax in enumerate(axes.flatten()):
        ax.scatter(x, tau_sorted, label='True tau', color='black', s=10, alpha=0.7)
        ax.scatter(x, preds_sorted[model_names[i]], label=model_names[i], color='tab:blue', s=10, alpha=0.7)
        ax.set_title(f'{model_names[i]}')
        ax.set_xlabel('Sample (sorted by tau)')
        ax.set_ylabel('ITE')
        ax.set_ylim(ymin, ymax)
        ax.legend()
    plt.tight_layout()
    plt.show()


def calc_by_package(X, treatment, y, tau):
    # X-learner
    learner_x = BaseXRegressor(learner=XGBRegressor())
    ate_x = learner_x.fit_predict(X=X, treatment=treatment, y=y)
    print('estimated causal effect, by X-learner: {:.04f}'.format(np.mean(ate_x)))

    # DML
    cf_dml = CausalForestDML(model_t=XGBRegressor(), model_y=XGBRegressor())
    cf_dml.fit(y, treatment, X=X)
    ate_dml = cf_dml.effect(X)
    print('estimated causal effect, by DML: {:.04f}'.format(np.mean(ate_dml)))

    # 拟合因果森林
    cf_cf = CausalRandomForestRegressor()
    cf_cf.fit(X, treatment, y)
    ate_cf = cf_cf.predict(X)
    print('estimated causal effect, by RandomForest: {:.04f}'.format(np.mean(ate_cf)))

    # 拟合因果树
    cf_cr = CausalTreeRegressor()
    cf_cr.fit(X, treatment, y)
    ate_cr = cf_cr.predict(X)
    print('estimated causal effect, by CausalTree: {:.04f}'.format(np.mean(ate_cr)))
    # 获取叶节点数量和对应的CATE
    print("叶节点数量:", cf_cr.tree_.n_leaves)
    leaf_ids = cf_cr.apply(X)
    unique_leaves = np.unique(leaf_ids)
    leaf_cate_dict = {}
    for leaf in unique_leaves:
        idx = (leaf_ids == leaf)
        treat_idx = idx & (treatment == 1)
        control_idx = idx & (treatment == 0)

        if treat_idx.sum() > 0 and control_idx.sum() > 0:
            cate = y[treat_idx].mean() - y[control_idx].mean()
        else:
            cate = np.nan  # 或者跳过该节点

        leaf_cate_dict[leaf] = cate

    for leaf, cate in leaf_cate_dict.items():
        print(f"叶节点 {leaf} 的 CATE: {cate}")

    # 合并结果
    df = pd.DataFrame({
        'y': y,
        'treat': treatment,
        'x-learner': np.ravel(ate_x),
        'DML': np.ravel(ate_dml),
        'CausalForest': np.ravel(ate_cf),
        'CausalTree': np.ravel(ate_cr)
    })
    df['tau_true'] = tau
    print('true causal effect: {}'.format(np.mean(tau)))

    # auuc
    auuc = auuc_score(df, outcome_col='y', treatment_col='treat', normalize=True, tmle=False)
    print(auuc)

    return df


if __name__ == '__main__':

    np.random.seed(0)

    # y-观测结果；X-样本特征；treatment-处理变量；tau-个体处理效应
    y, X, treatment, tau, b, e = synthetic_data(mode=2, p=25)

    result_df = calc_by_package(X, treatment, y, tau)

    plot_sorted_tau_and_preds(result_df)

    # 绘制auuc曲线
    plot_gain(
        result_df,
        outcome_col='y',
        treatment_col='treat',
        normalize=True,
        random_seed=10,
        n=100,
        figsize=(8, 8)
    )

    plt.show()

结果解读：

ATE结果：结果较为意外，因果树的预测更接近真值，但这一结论并不具备普适性。例如，将数据中的p（协变量数量）由25增加到40时，因果森林的ATE指标会更接近真值。

estimated causal effect, by X-learner: 0.7352
estimated causal effect, by DML: 0.5525
estimated causal effect, by RandomForest: 0.6582
estimated causal effect, by CausalTree: 0.6999
true causal effect: 0.7946483837099231

ITE结果：因果树仅保留7个叶节点，因此ITE仅有7个离散值（0位置附近，有两个值）；而因果森林通过多棵树平均效应，使ITE分布更加均衡。

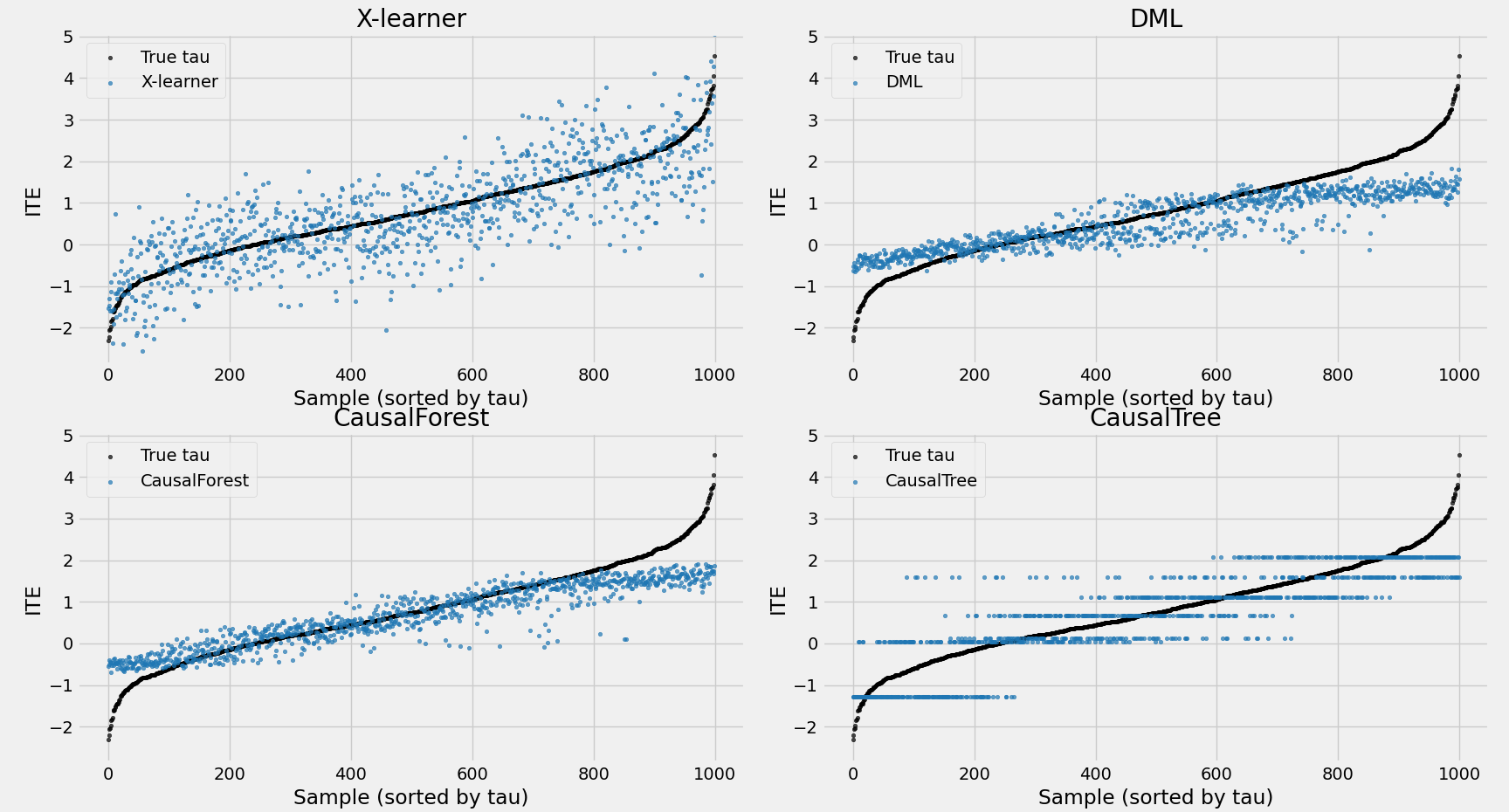
叶节点数量: 7
叶节点 4 的 CATE: -1.2794264565485223
叶节点 5 的 CATE: 0.04997737614570308
叶节点 7 的 CATE: 0.6736109791416229
叶节点 8 的 CATE: 0.12112326235879434
叶节点 10 的 CATE: 1.1193301595067435
叶节点 11 的 CATE: 2.0795258688365204
叶节点 12 的 CATE: 1.5968641890556292

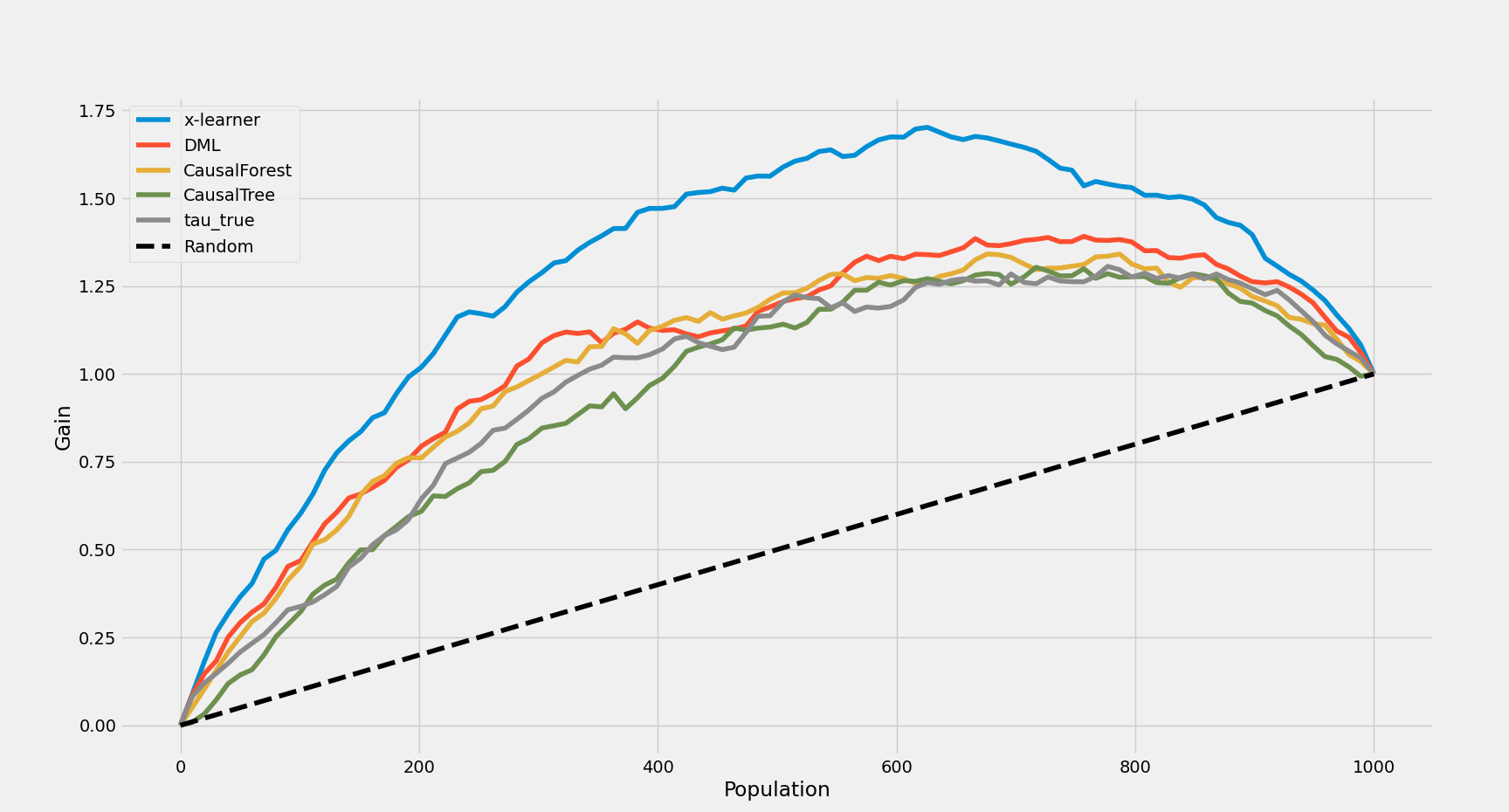
AUUC结果：因果森林在排序能力上优于因果树。AUUC关注模型在ITE较高个体（图右上部分）上排序的准确性。从ITE分布图可见，因果森林认为ITE较大的样本，其真实值普遍分布在右侧；而因果树预测的最大值则横跨600以上区间。

x-learner       1.281181
DML             1.059788
CausalForest    1.026942
CausalTree      0.941297
tau_true        0.971806

5 总结

正文到此结束，核心内容总结如下：

因果森林模型能够有效评估异质性因果效应，适用于因果推断任务中个体化或分群处理效应的估计。
因果森林的基础构件是因果树，其核心思想是通过寻找最优分割点，使不同叶节点的CATE（条件平均处理效应）差异最大化，从而揭示处理效应的异质性。

6 相关阅读

Recursive partitioning for heterogeneous causal effects：https://www.pnas.org/doi/10.1073/pnas.1510489113

Estimation and Inference of Heterogeneous Treatment Effects using Random Forests：https://www.tandfonline.com/doi/full/10.1080/01621459.2017.1319839

决策树入门、sklearn实现、原理解读和算法分析：https://mp.weixin.qq.com/s/PbtFMBylahNSKteiBClEZw

随机森林原理和性能分析：https://mp.weixin.qq.com/s/E9izVenKjmp4jCnpFw51rA

因果推断 | 元学习方法原理详解和代码实操：https://mp.weixin.qq.com/s/zA5PU0uXw-ZMOKJPBNyBJg

因果推断 | 从因果树到因果森林：理论解析与代码实践