(done) 自学 cuda (3) 实现神经网络前向传播

url: https://www.bilibili.com/video/BV1Wgcoe4EUu?from_spmid=default-value&plat_id=411&share_from=season&share_medium=android_hd&share_plat=android&share_session_id=a537754f-6467-415f-a6a0-fd787ed5fdfb&share_source=COPY&share_tag=s_i&spmid=united.player-video-detail.0.0&timestamp=1739109177&unique_k=LvsUicJ&vd_source=7a1a0bc74158c6993c7355c5490fc600&spm_id_from=333.788.videopod.sections

如下图，是单个输入在单层神经网络上的计算：
（其实这里 X 矩阵和 W 矩阵放反了，应该是 Wx + b 而不是 xW + b）

由于输入往往按批次给，因此也可以把输入堆叠成矩阵：
（其实这里 X 矩阵和 W 矩阵放反了，应该是 Wx + b 而不是 xW + b）
（因此x矩阵的列数等于输入的个数）

算子编写如下：

// forward 公式: Wx + b
// batch_size 输入矩阵的列数，表示一个batch中样本的数量，也是输出矩阵的列数
// n 输入矩阵的行数，也是权重矩阵的列数，表示每个样本的特征数量
// out_w 权重矩阵的行数，表示这一层神经元输出的特征数量，即输出矩阵的行数
// input 输入矩阵，大小为 (n, batch_size)
// weights 权重矩阵，大小为 (out_w, n)
// biases 偏置向量，大小为 (out_w, 1)  实际计算中会扩展为输出矩阵的大小 (out_w, batch_size)
// output 输出矩阵，大小为 (out_w, batch_size)
__global__ void forward(int batch_size, int n, int out_w, float* input, float* weights, float* biases, float* output)
{
  // 这里的 row 和 column 可以分别对应输出矩阵的行和列，输出矩阵每一个元素的计算都是相同且独立的
  int column = blockIdx.x*blockDim.x + threadIdx.x;
  int row = blockIdx.y*blockDim.y + threadIdx.y;
  if (row < batch_size && column < out_w)
  {
    // TODO: 这里感觉 row 和 column 的命名反了，更符合直觉的应该是 row 对应 out_w，column 对应 batch_size
    output[row*out_w+column] = biases[column];
    for(int i = 0; i < n; i++)
    {
      output[row*out_w+column] += weights[i*out_w + column] * input[row*n + i];
    }
  }
}

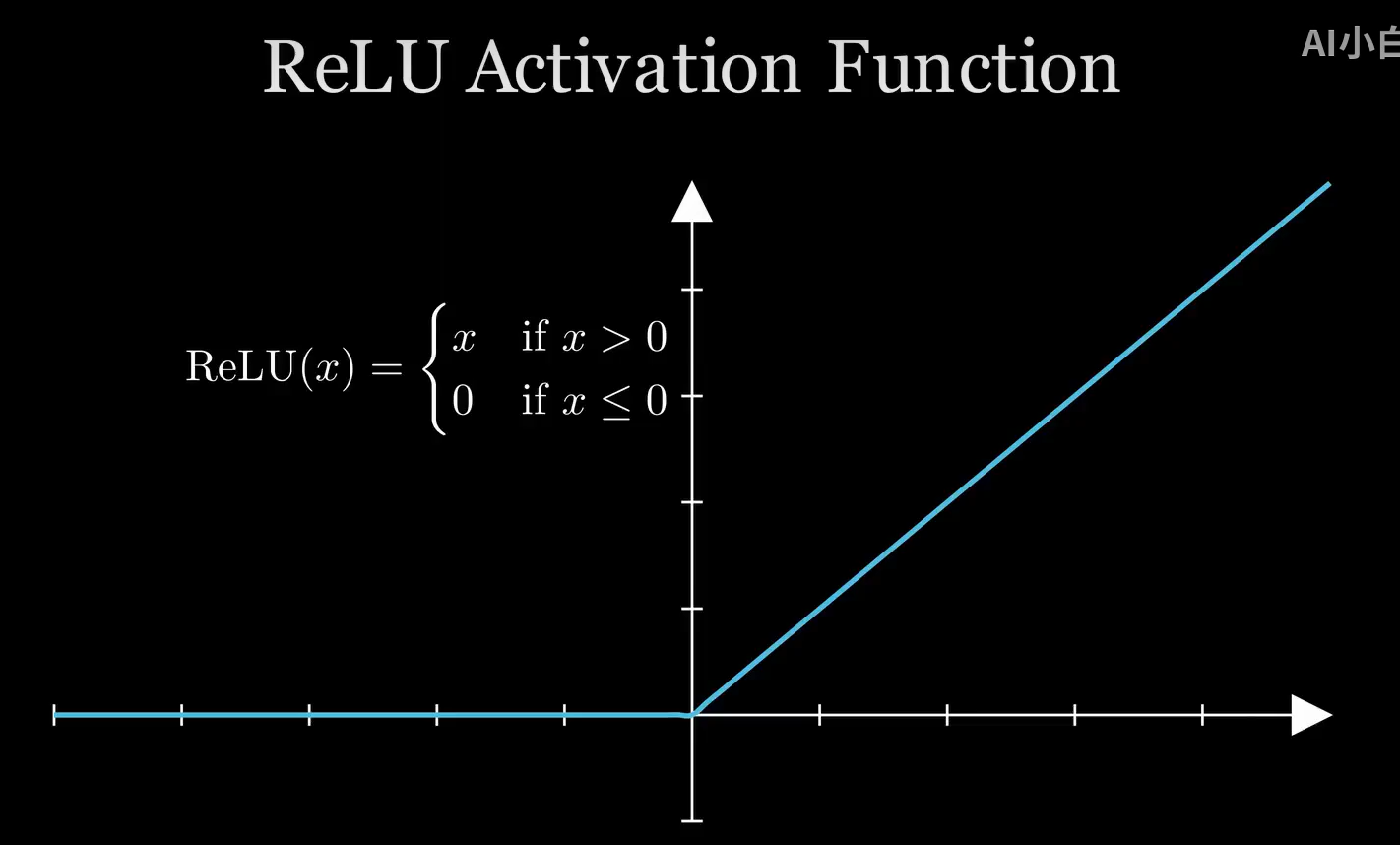
接下来是编写激活函数算子，常用的激活函数是 ReLU 函数，如下图：

算子编写如下，很简单：

__global__ void relu(int w, int h, float* a, float* b)
{
  int column = blockIdx.x*blockDim.x + threadIdx.x;
  int row = blockIdx.y*blockDim.y + threadIdx.y;
  if (row < h && column < w)
  {
    float activation = a[row*w+column];
    b[row*w+column] =  activation > 0.f ? activation : 0.f;
  }
}

目前我们的最后一层神经元输出层只会输出一些不明所以的浮点数。考虑到我们神经网络用途是识别手写数字，也就是分类，因此最后需要加一个函数把不明所以的浮点数转换为概率分布。

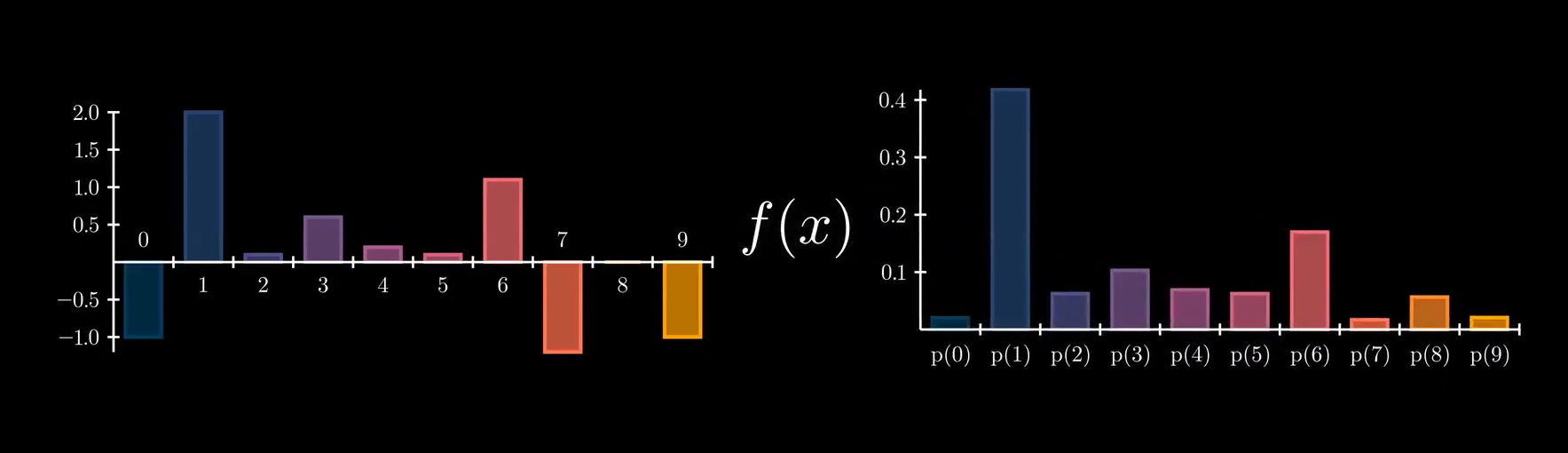
通常使用 softmax 作为最终的激活函数来达到这个效果

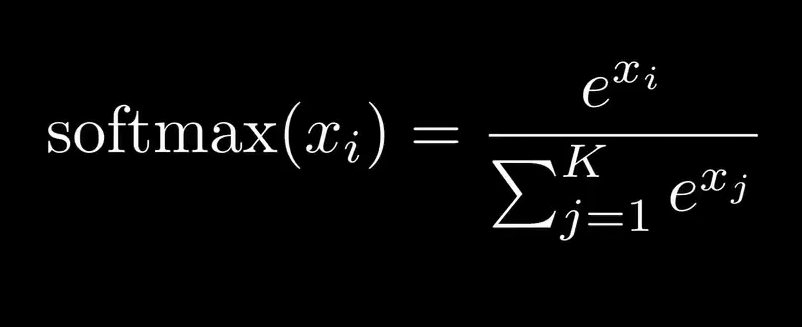
需要注意的是，这里的分子分母都是指数函数，而指数函数的特性是指数增长，如果 x 的值有多个正值，就会导致指数溢出，因为在分母中累加了很多大数。
可以通过在指数中减去最大值缓解这个问题，如下：
如此一来，指数总是负的，那么 e^x 的值就会保持在 0 ~ 1

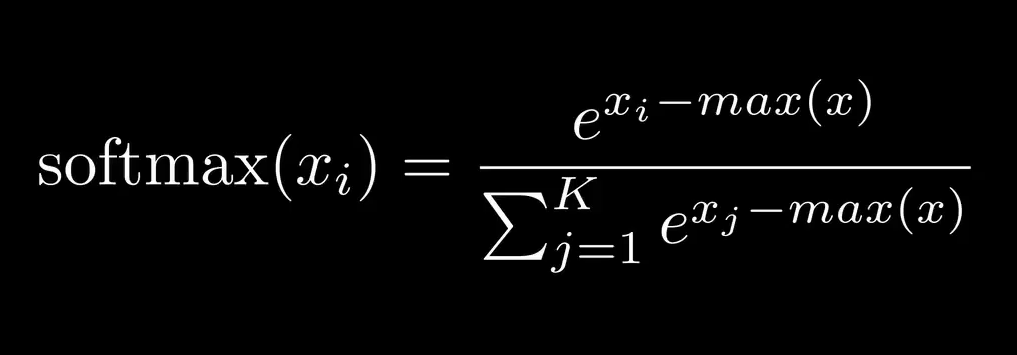
代码如下：

__global__ void softmax(int w, int h, float* a, float* b)
{
  int col = blockIdx.x*blockDim.x + threadIdx.x;
  int row = blockIdx.y*blockDim.y + threadIdx.y;
  if (row < h && col < w)
  {
    float maxval = a[row*w];
    for (int i = 1; i<w; i++)
    {
      maxval = max(maxval, a[row*w + i]);
    }
    float divisor = 0.f;
    for (int i = 0; i<w; i++)
    {
      divisor += exp(a[row*w + i] - maxval);
    }
    b[row*w + col] = exp(a[row*w + col]-maxval)/(divisor);
  }
}

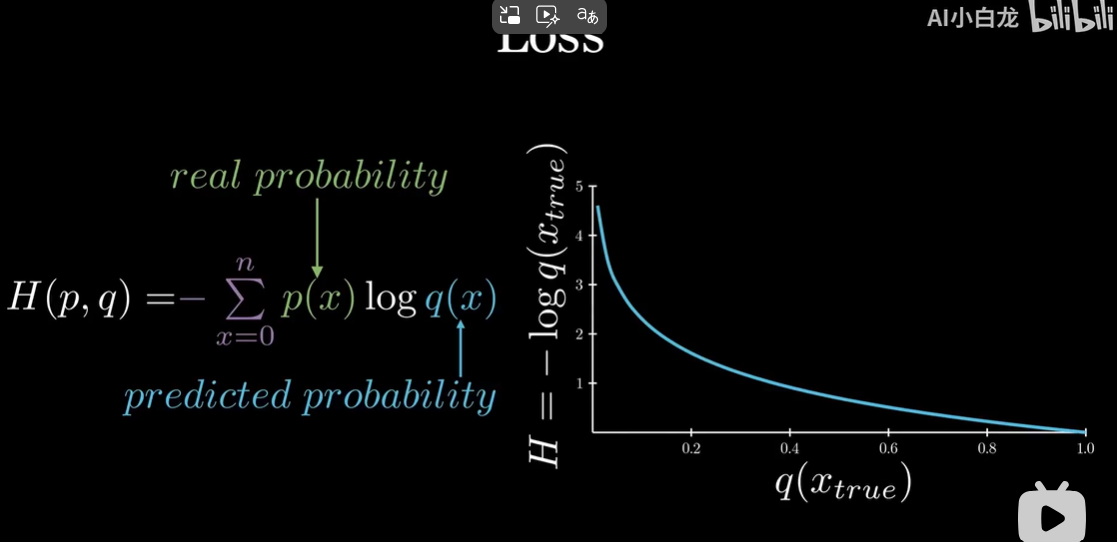
神经网络最后一个组成部分是损失函数：
我们使用交叉熵损失函数

由于真实概率来源于样本，是 0 或 1，因此损失函数还能继续简化。
最后如右图，当神经网络预测的结果接近真实情况时，损失函数趋近于 0

代码如下：

__global__ void cross_entropy(int w, int h, float* preds, float* real, float* output)
{
  int idx = blockIdx.x*blockDim.x + threadIdx.x;
  if (idx < h)
  {
    float loss = 0.f;
    for (int i = 0; i<w; i++)
    {
      loss -= real[idx*w + i] * log(max(1e-6, preds[idx*w + i]));
    }
    output[idx] = loss;
  }
}

最后需要注意的是，我们的权重矩阵需要被初始化为某个随机值

__global__ void init_rand(int w, int h, float* mat)
{
  int column = blockIdx.x*blockDim.x + threadIdx.x;
  int row = blockIdx.y*blockDim.y + threadIdx.y;
  if (row < h && column < w)
  {
    curandState state;
    curand_init(42, row*w+column, 0, &state);
    mat[row*w + column] = curand_normal(&state)*sqrtf(2.f/h);
  }
}

mnist.cu 代码整体解析，见后边