梯度下降法 (Gradient Descent, GD)
核心思想:沿着当前点梯度方向的反方向(即函数下降最快的方向)前进一小步,逐步逼近极小值。
推导:
目标:最小化函数 F(x)F(\mathbf{x})F(x)。
在当前位置 xk\mathbf{x}_kxk 对函数进行一阶泰勒展开:
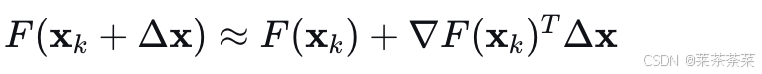
为了使函数值减小,我们需要 ∇F(xk)TΔx<0\nabla F(\mathbf{x}_k)^T \Delta \mathbf{x} < 0∇F(xk)TΔx<0。最速下降方向是 Δx=−∇F(xk)\Delta \mathbf{x} = -\nabla F(\mathbf{x}_k)Δx=−∇F(xk)。
因此迭代公式为:
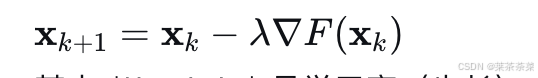
其中 λ\lambdaλ 是学习率(步长)。
优缺点:
优点:
实现简单,计算量小,只需计算一阶梯度。
内存需求小,适用于大规模问题。
缺点:
收敛速度慢,特别是接近最优点时,呈线性收敛。
“锯齿状”路径:连续的梯度方向是正交的,导致优化路径曲折。
对学习率敏感:学习率太小则收敛慢,太大则可能震荡甚至发散。
牛顿法 (Newton’s Method)
核心思想:在当前位置对函数进行二阶泰勒展开,并用该二次函数的最小点来近似原函数的最小点。它同时利用了梯度(一阶信息)和曲率(二阶信息)。
推导:
在 xk\mathbf{x}_kxk 处进行二阶泰勒展开:
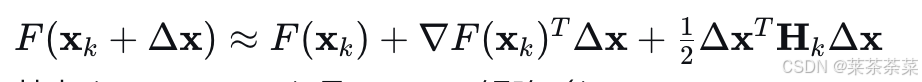
其中 Hk\mathbf{H}kHk 是 Hessian 矩阵([H]ij=∂2F∂xi∂xj[\mathbf{H}]{ij} = \frac{\partial^2 F}{\partial x_i \partial x_j}[H]ij=∂xi∂xj∂2F)。
为了最小化这个二次近似函数,令其关于 Δx\Delta \mathbf{x}Δx 的导数为零:

解得最优步长 Δx=−Hk−1∇F(xk)\Delta \mathbf{x} = -\mathbf{H}_k^{-1} \nabla F(\mathbf{x}_k)Δx=−Hk−1∇F(xk)。
因此迭代公式为:

优缺点:
优点:
收敛速度快,具有二阶收敛速度(如果 Hessian 矩阵正定),远快于梯度下降。
无需选择学习率,步长由 Hessian 矩阵自动确定。
缺点:
计算和存储开销巨大:需要计算和存储 O(n2)O(n^2)O(n2) 的 Hessian 矩阵并求其逆(O(n3)O(n^3)O(n3)),对于高维问题不可行。
要求 Hessian 矩阵正定,否则可能收敛到鞍点或极大值点。在实际应用中,Hessian 矩阵很可能非正定。
高斯-牛顿法 (Gauss-Newton, GN)
核心思想:牛顿法的简化形式,专门用于求解非线性最小二乘问题 minx12∣∣r(x)∣∣22\min_{\mathbf{x}} \frac{1}{2} ||\mathbf{r}(\mathbf{x})||_2^2minx21∣∣r(x)∣∣22,其中 r(x)\mathbf{r}(\mathbf{x})r(x) 是残差向量。它用雅可比矩阵近似 Hessian 矩阵,避免了直接计算 Hessian。
推导:
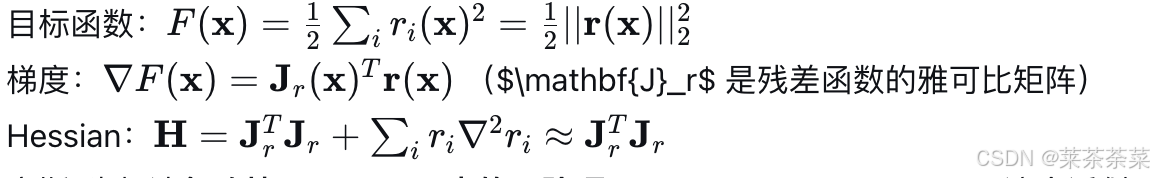
高斯-牛顿法忽略掉了 Hessian 中的二阶项 ∑iri∇2ri\sum_i r_i \nabla^2 r_i∑iri∇2ri。这个近似在残差 rir_iri 很小或者函数接近线性时是合理的。
将近似 Hessian 和梯度代入牛顿法公式:
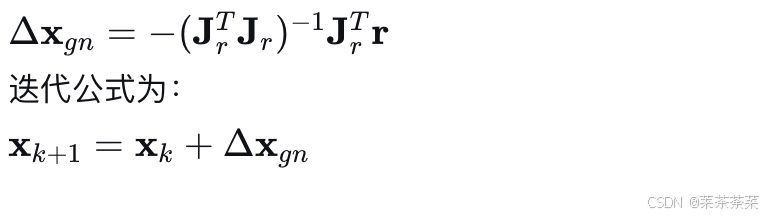
优缺点:
优点:
无需计算 Hessian 矩阵,只需计算雅可比矩阵,计算量大为降低。
比梯度下降快得多。
缺点:
近似可能不准确,只有残差很小或接近线性时效果才好。
矩阵 JrTJr\mathbf{J}_r^T \mathbf{J}_rJrTJr 可能是奇异(不可逆)或病态的,导致算法失败。
列文伯格-马夸尔特法 (Levenberg-Marquardt, LM)
核心思想:高斯-牛顿法的稳健改进版本。它引入了阻尼因子 μ\muμ,在梯度下降和高斯-牛顿法之间自适应平滑切换,解决了 GN 法的不稳定问题。
推导:
LM 法的核心是求解以下带阻尼的正规方程:
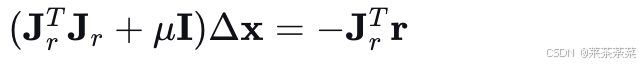
其中 μ>0\mu > 0μ>0 是阻尼因子,I\mathbf{I}I 是单位阵。
当 μ→0\mu \to 0μ→0 时,方程变为 (JrTJr)Δx=−JrTr(\mathbf{J}_r^T \mathbf{J}_r) \Delta \mathbf{x} = -\mathbf{J}_r^T \mathbf{r}(JrTJr)Δx=−JrTr,即 高斯-牛顿步。
当 μ→∞\mu \to \inftyμ→∞ 时,方程变为 μIΔx=−JrTr\mu \mathbf{I} \Delta \mathbf{x} = -\mathbf{J}_r^T \mathbf{r}μIΔx=−JrTr,即 Δx≈−1μJrTr\Delta \mathbf{x} \approx -\frac{1}{\mu} \mathbf{J}_r^T \mathbf{r}Δx≈−μ1JrTr,这是梯度下降步(方向与梯度下降相同,步长为 1/μ1/\mu1/μ)。
迭代过程:
计算当前参数 xk\mathbf{x}_kxk 下的残差 F(xk)F(\mathbf{x}_k)F(xk) 和雅可比矩阵 Jr\mathbf{J}_rJr。
求解方程 (JrTJr+μI)Δx=−JrTr(\mathbf{J}_r^T \mathbf{J}_r + \mu \mathbf{I}) \Delta \mathbf{x} = -\mathbf{J}_r^T \mathbf{r}(JrTJr+μI)Δx=−JrTr,得到 Δx\Delta \mathbf{x}Δx。
计算候选点 xcandidate=xk+Δx\mathbf{x}_{candidate} = \mathbf{x}k + \Delta \mathbf{x}xcandidate=xk+Δx 及其残差 F(xcandidate)F(\mathbf{x}{candidate})F(xcandidate)。
增益比 ρ=F(xk)−F(xcandidate)ΔxT(μΔx−JrTr)\rho = \frac{F(\mathbf{x}k) - F(\mathbf{x}{candidate})}{\Delta \mathbf{x}^T (\mu \Delta \mathbf{x} - \mathbf{J}_r^T \mathbf{r})}ρ=ΔxT(μΔx−JrTr)F(xk)−F(xcandidate) (实际下降 / 预测下降)
如果 ρ\rhoρ 很大(>0.75),说明二次近似模型很好,接受这一步,并减小 μ\muμ(例如 μ:=μ/3\mu := \mu / 3μ:=μ/3),下次迭代更接近高斯-牛顿法(更快)。
如果 ρ\rhoρ 很小(<0.25),说明模型近似很差,拒绝这一步,并增大 μ\muμ(例如 μ:=2μ\mu := 2\muμ:=2μ),下次迭代更接近梯度下降(更稳健)。
如果 ρ\rhoρ 适中,则接受这一步,但保持 μ\muμ 不变。
优缺点:
优点:
非常强大和稳健,是求解非线性最小二乘问题的标准算法。
可以处理 Jacobian 矩阵奇异或病态的情况,因为 (JTJ+μI)(\mathbf{J}^T\mathbf{J} + \mu \mathbf{I})(JTJ+μI) 总是正定的。
自适应性强,能在快速收敛(GN模式)和稳健性(GD模式)之间自动切换。
缺点:
相比高斯-牛顿法,计算量稍大(需要求解带阻尼的方程)。
对于超大规模问题,求解线性方程组 (JTJ+μI)Δx=−JTr(\mathbf{J}^T\mathbf{J} + \mu \mathbf{I}) \Delta \mathbf{x} = -\mathbf{J}^T \mathbf{r}(JTJ+μI)Δx=−JTr 可能仍然是瓶颈。
总结对比
方法 核心思想 优点 缺点 适用场景
梯度下降 (GD) 一阶近似,沿负梯度方向 实现简单,内存开销小 收敛慢,对步长敏感 大规模问题,深度学习
牛顿法 (Newton) 二阶近似,使用完整Hessian 收敛速度极快(二阶) 计算存储开销巨大,需H正定 中小规模、Hessian易求的问题
高斯-牛顿 (GN) 用于最小二乘,用JTJJ^TJJTJ近似H 比GD快,免于计算Hessian 可能不稳定(JTJJ^TJJTJ奇异) 中小规模非线性最小二乘
LM GN + 阻尼因子 强大、稳健、自适应 比GN计算量稍大 非线性最小二乘的标准选择
演进关系:梯度下降 → 牛顿法 → (针对最小二乘问题) → 高斯-牛顿法 → (增加稳健性) → 列文伯格-马夸尔特法。
在实际应用中,LM算法因其卓越的稳健性和效率,通常是解决中小规模非线性最小二乘问题(如计算机视觉中的Bundle Adjustment、曲线拟合)的首选方法。对于超大规模问题(如神经网络训练),随机梯度下降(SGD)及其变体因其极低的内存和计算复杂度而占主导地位。