一.什么是树形DP?
简单来说,树形DP就是在树结构上进行状态转移的一种思想。一般是根据子树的状态更新父亲的状态,进行状态转移,跟分治的思想非常像。
二.树形DP例题
1.树的最长路径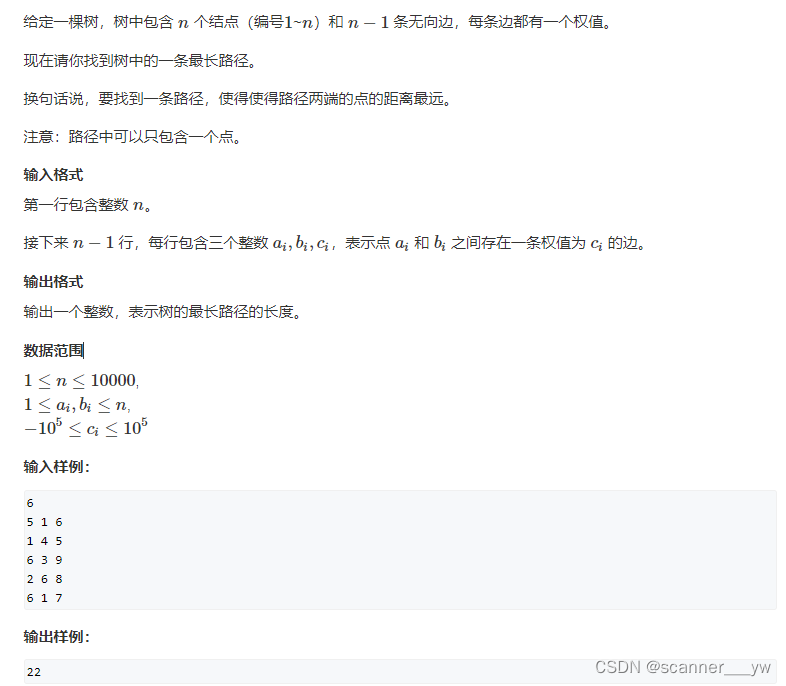
题意分析:首先树有一个很重要的性质:树上任意点能到的最远点,一定是树的直径的某个端点,因此本题就是让我们求树的直径。因此我们只需要知道以某个点向其他方向的最远距离 + 某个点向下的最远距离,就可以知道树的直径是多少。
对于求向下最远距离,我们只需要dfs算出深度就可以了,那么如何求解其他方向的最远距离呢?对于这个问题,我们看树上直径的图,实际上会是一条链。
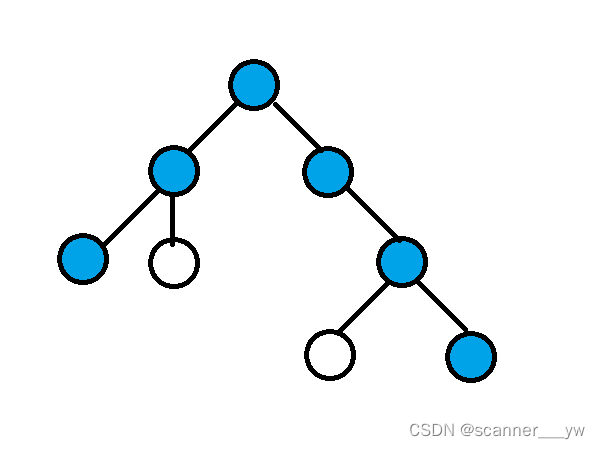
比如说这个图,我们能明显看出来,这条直径一定是通过某个点挂起来的,就像那种晒衣架一样,我们只需要保证对于某个点不经过重复的一颗子树获得的最大的距离和次大距离,则一定是以这个点其他方向或者向下扩展了,则此时答案就是最大距离和最小距离的和。
代码实现:
#include "bits/stdc++.h"
using namespace std;
struct node{
int nxt;
int to;
int wi;
}e[20010];
int idx,he[10010],ans = -1e9;
void add(int u,int v,int w)
{
e[++idx].nxt = he[u];
e[idx].to = v;
e[idx].wi = w;
he[u] = idx;
}
int dfs(int cur,int fa)
{
int d1 = 0,d2 = 0,dis = 0;
for(int i = he[cur];~i;i = e[i].nxt){
if(e[i].to == fa) continue;
int d = dfs(e[i].to,cur) + e[i].wi;
if(d >= d1) d2 = d1,d1 = d;
else if(d > d2) d2 = d;
dis = max(d,dis);
}
ans = max(d1 + d2,ans);
return dis;
}
void init(int n)
{
for(int i = 1;i <= n;i++) he[i] = -1;
}
int main()
{
int n,u,v,w;
cin >> n;
init(n);
for(int i = 1;i < n;i++) {
cin >> u >> v >> w;
add(u,v,w);add(v,u,w);
}
dfs(1,-1);
cout << ans << endl;
return 0;
}2.树的中心(换根DP)
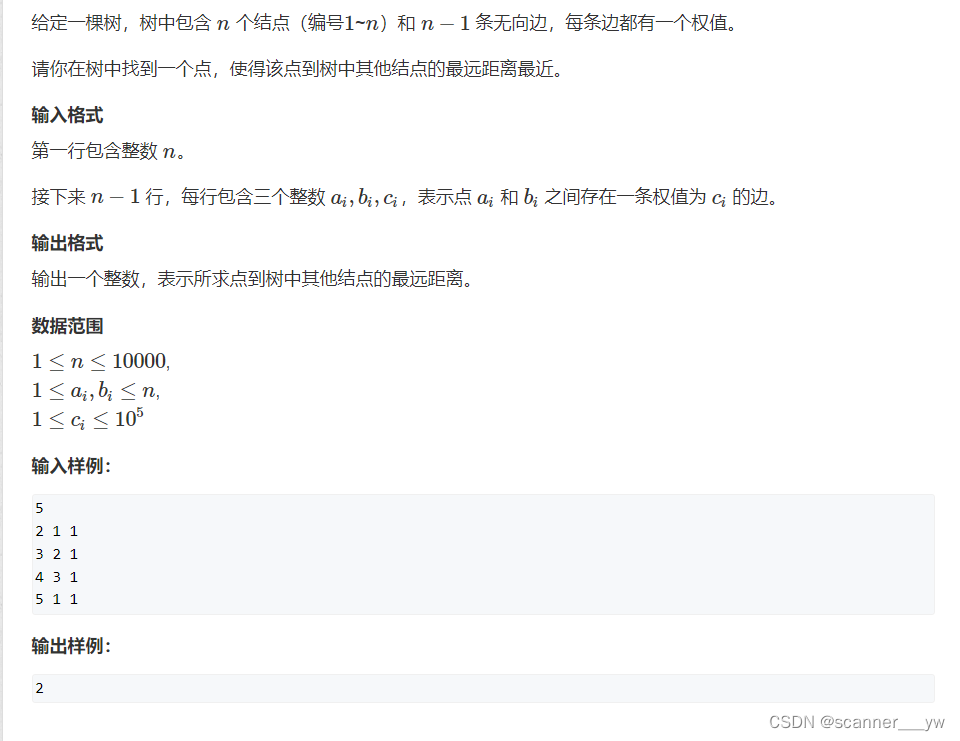
题意分析:此题给定我们一颗树,让我们求树中一个点到其他点的最远距离最近,也就是中心。
这个题的做法和上个题非常类似,是以一个点为中心,往上和往下遍历,找到最远的距离。因此我们需要向下dfs一遍,向上dfs一遍求出最远距离。对于向下求解最远距离,我们利用父节点信息更新子节点信息即可;对于向上求解最远距离,我们利用子节点更新父亲节点的信息即可。(注意:当我们向上dfs的时候,如果发现当前节点在父亲节点的最长路径里面,那么就不能用当前节点的最大值去更新父亲节点,而应当用次大值去更新父亲节点的信息。
图解:
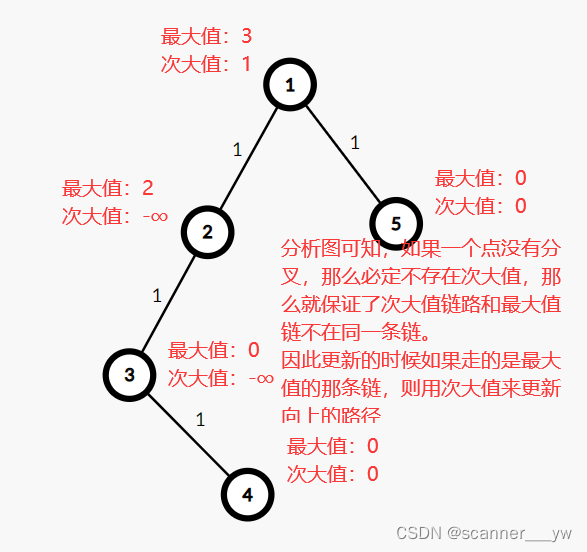
代码实现:
#include "bits/stdc++.h"
using namespace std;
struct node{
int nxt;
int to;
int wi;
}e[20010];
int idx,he[10010],ans = -1e9;
void add(int u,int v,int w)
{
e[++idx].nxt = he[u];
e[idx].to = v;
e[idx].wi = w;
he[u] = idx;
}
int dfs(int cur,int fa)
{
int d1 = 0,d2 = 0,dis = 0;
for(int i = he[cur];~i;i = e[i].nxt){
if(e[i].to == fa) continue;
int d = dfs(e[i].to,cur) + e[i].wi;
if(d >= d1) d2 = d1,d1 = d;
else if(d > d2) d2 = d;
dis = max(d,dis);
}
ans = max(d1 + d2,ans);
return dis;
}
void init(int n)
{
for(int i = 1;i <= n;i++) he[i] = -1;
}
int main()
{
int n,u,v,w;
cin >> n;
init(n);
for(int i = 1;i < n;i++) {
cin >> u >> v >> w;
add(u,v,w);add(v,u,w);
}
dfs(1,-1);
cout << ans << endl;
return 0;
} 3.数字转换 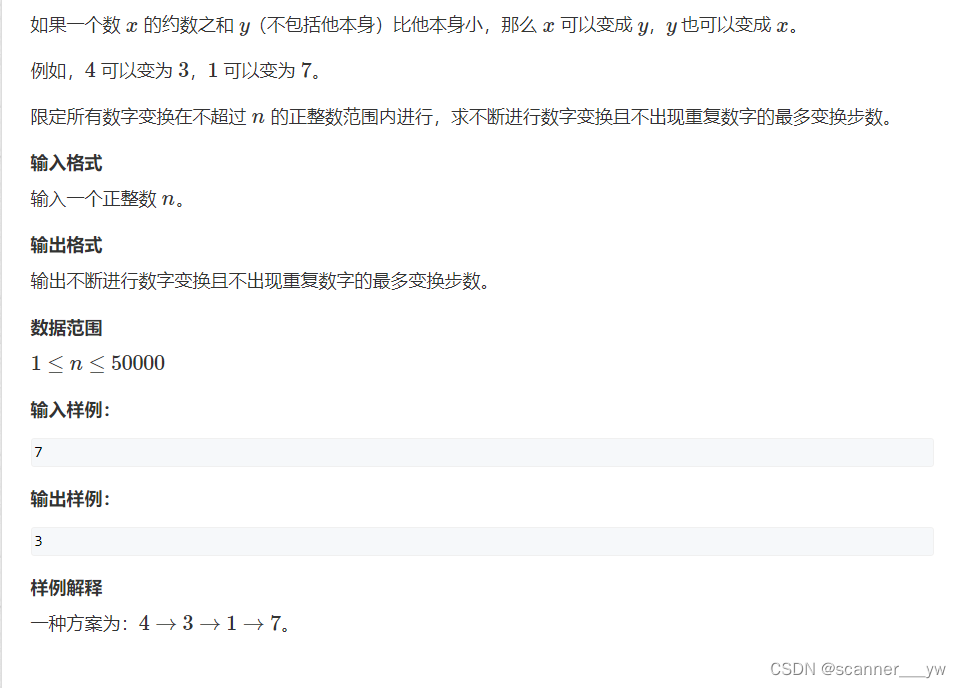
题意:这个题让我们首先处理一个树的约数,如果一个数的约数和小于他本身的话,那么就会存在一条约束和----->他本身的路径,最后我们建立树模型求解一个最长直径就可以了。(我们求解最长直径的时候,以1为根节点进行搜索,因为对于任何一个数,如果他是质数,那么他的约束和必定是一,因此一定挂在1这个根节点上;如果这个数是个合数,那么他一定能分解成为质数相乘,必定会挂在质数上面,因此一定会挂在1这棵树上。
代码实现:
#include "bits/stdc++.h"
using namespace std;
const int N = 50010;
struct node{
int nxt;
int to;
}e[N];
int he[N],sum[N],cnt,ans;
void add(int a,int b)
{
e[++cnt].nxt = he[a];
e[cnt].to = b;
he[a] = cnt;
}
int dfs(int u)
{
int d1 = 0,d2 = 0;
for(int i = he[u];~i;i = e[i].nxt) {
int to = e[i].to;
int d = dfs(to) + 1;
if(d >= d1) d2 = d1,d1 = d;
else if(d > d2) d2 = d;
}
ans = max(ans,d1 + d2);
return d1;
}
int main()
{
int n;
cin >> n;
memset(he,-1,sizeof(he));
for(int i = 1;i <= n;i++) {
for(int j = 2;j <= n / i;j++) {
sum[i * j] += i;
}
}
for(int i = 2;i <= n;i++) if(sum[i] < i) add(sum[i],i);
dfs(1);
cout << ans << endl;
return 0;
}4.二叉苹果树
题意:给定你n个数,n-1条边,q个点,问你保留q个点的最大价值为多少。我们可以拟定如果下dp数组,dp[i][j]为以i点为根节点,保留j个节点的最大价值是多少。又因为对于每一个节点我们想要保留他这个节点,那么一定会保留他的父亲节点。因此这是一个树上的分组背包问题。
故状态转移方程为dp[i][j] = max(dp[i][j],dp[i][j - k - 1][j] + e[i].wi + dp[son][k])
代码实现:
#include "bits/stdc++.h"
using namespace std;
const int N = 110;
struct node{
int nt;
int to;
int wi;
}e[N << 1];
int dp[N][N],he[N],cnt;
int m,n;
void add(int a,int b,int c)
{
e[++cnt].nt = he[a];
e[cnt].to = b;
e[cnt].wi = c;
he[a] = cnt;
}
//acwing1074
//类似于有依赖的背包,首先枚举子树(物品组),然后枚举操作数(体积),最后枚举选择(决策)
void dfs(int u,int fa)
{
for(int i = he[u];~i;i = e[i].nt){
int son = e[i].to;
if(son == fa) continue;
dfs(son,u);
for(int j = m;j >= 1;j--){
for(int k = 0;k < j;k++) {
dp[u][j] = max(dp[u][j],dp[u][j - k - 1] + e[i].wi + dp[son][k]);
}
}
}
}
int main()
{
cin >> n >> m;
memset(he,-1,sizeof(he));
for(int i = 1;i < n;i++) {
int a,b,c;
cin >> a >> b >> c;
add(a,b,c);
add(b,a,c);
}
dfs(1,-1);
cout << dp[1][m] << endl;
return 0;
}5.战略游戏

题意:对于每一个节点我们都能够放置一个守卫,可以看他与他连边的所有点,问我们整棵树的所有点互相能看到最少需要放置多少个守卫。
对于这个题目,我们拟定状态转移数组为dp[i][j],表达以i为根,j有两个状态(0,1), 表示我当前放置守卫和不放置守卫的。
那么对于这个转移状态可以表示为
1.如果我当前节点不放守卫,那么我的连边节点必须放置守卫。
dp[i][0] += dp[son][1];
2.如果我们当前节点放置守卫,那么我们子节点可以放置守卫,也可以不放置守卫。
dp[i][1] += min(dp[son][0],dp[son][1]);
代码实现:
#include "bits/stdc++.h"
using namespace std;
const int N = 1510;
struct node{
int nt;
int to;
}e[N << 1];
int dp[N][N],he[N],idx,vs[N],n;
//战略游戏acwing323
void add(int a,int b)
{
e[++idx].to = b;
e[idx].nt = he[a];
he[a] = idx;
}
void dfs(int cur)
{
dp[cur][0] = 0;
dp[cur][1] = 1;
for(int i = he[cur];~i;i = e[i].nt) {
int to = e[i].to;
dfs(to);
dp[cur][0] += dp[to][1];
dp[cur][1] += min(dp[to][0],dp[to][1]);
}
}
int main()
{
while(scanf("%d",&n) != -1) {
int p,cnt,x;
idx = 0;
memset(he,-1,sizeof(he));
memset(vs,0,sizeof(vs));
for(int k = 1;k <= n;k++){
scanf("%d:(%d)",&p,&cnt);
for(int i = 1;i <= cnt;i++) {
scanf("%d",&x);
add(p,x);
vs[x] = 1;
}
}
int root = 0;
for(int i = 0;i < n;i++) if(!vs[i]) root = i;
dfs(root);
printf("%d\n",min(dp[root][1],dp[root][0]));
}
return 0;
}6.皇宫看守

题意:该题和上题不一样的是,我们各个节点不需要相互看到,只需要最小覆盖到整棵树就可以了。因此对于状态方程的思考,我们还需要考虑多一个状态,那就是当前节点不放置守卫,后面节点放置守卫看到当前节点的最小价值是多少。
我们定义dp[i][j](j分别为0,1,2),
0表示当前节点被父亲节点看到了
1表示当前节点被子节点看到了
2表示当前节点放置守卫
1.对于当前节点被父亲节点看到
状态方程为:dp[i][0] += min(dp[son][1],dp[son][2]);
2.对于当前节点被子节点看到了
状态方程为:min(dp[i][1],dp[son][2] + dp[i][0] - min(dp[son][1],dp[son][2]));
3.对于当前节点放置守卫
状态方程为:dp[i][j] += min({dp[son][0],dp[son][1],dp[son][2]})
三.总结
本周学习了树形dp,并且刷了几个经典例题,感觉重在表达状态方程,树形dp比较于状压dp来说更好理解转移状态。
题目链接: