根轨迹:
“根”和“极点”类似。
根的作用:
影响系统的变化趋势。
所以可通过设计【补偿器】来改变【根】,从而改变系统的输出。
【根】对系统变化趋势的影响(【根】的变化规律):
一阶系统:
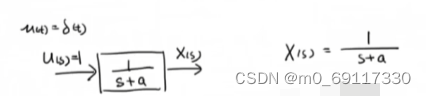
求得该系统的【根】为-a:
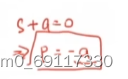
则该系统的输出曲线为:

把【根】在【复平面】上表达出来。则【根】如果在负方向上,则系统输出是衰减的;【根】如果在正方向上,则系统输出是增加的。且【根】绝对值越大,衰减/增加越快。
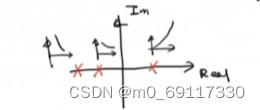
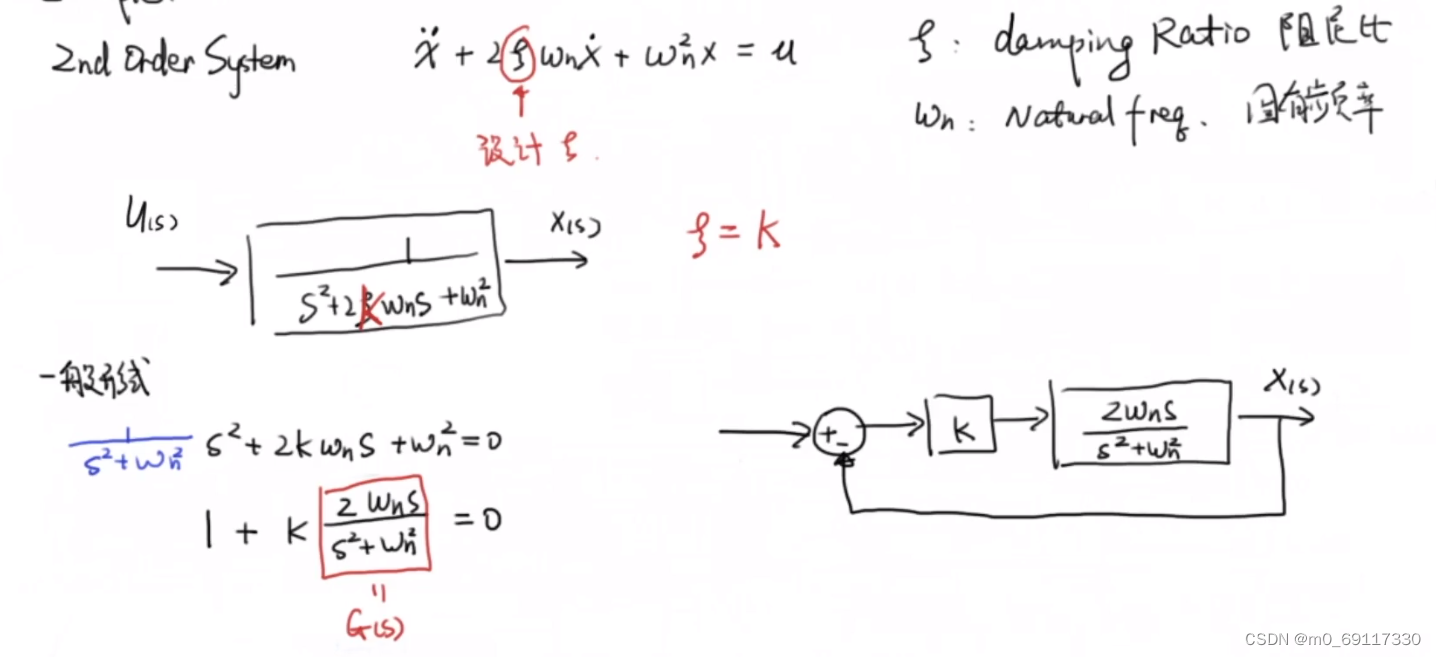
二阶系统:
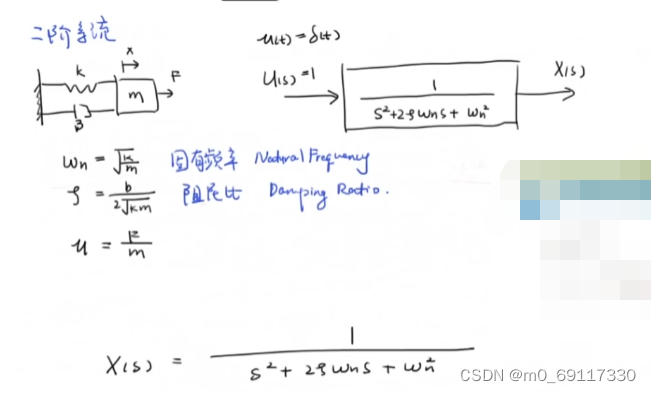
求得该系统的【根】为:
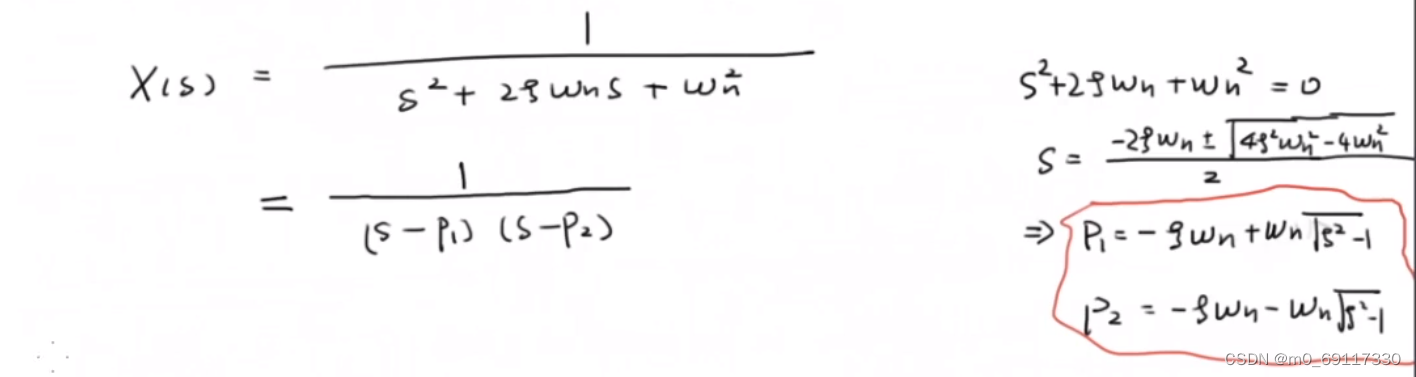
讨论该系统的输出且把【根】在【复平面】上表达出来:
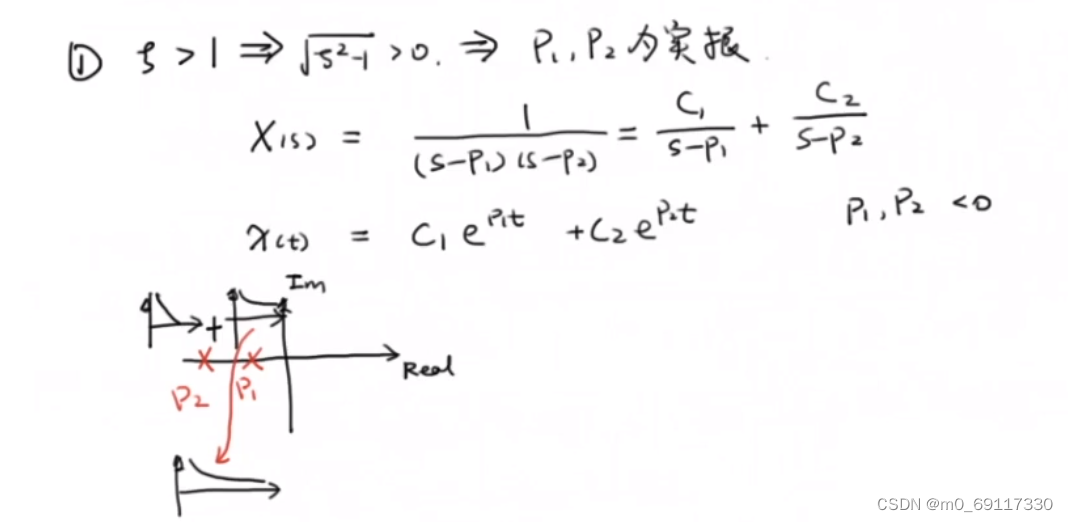
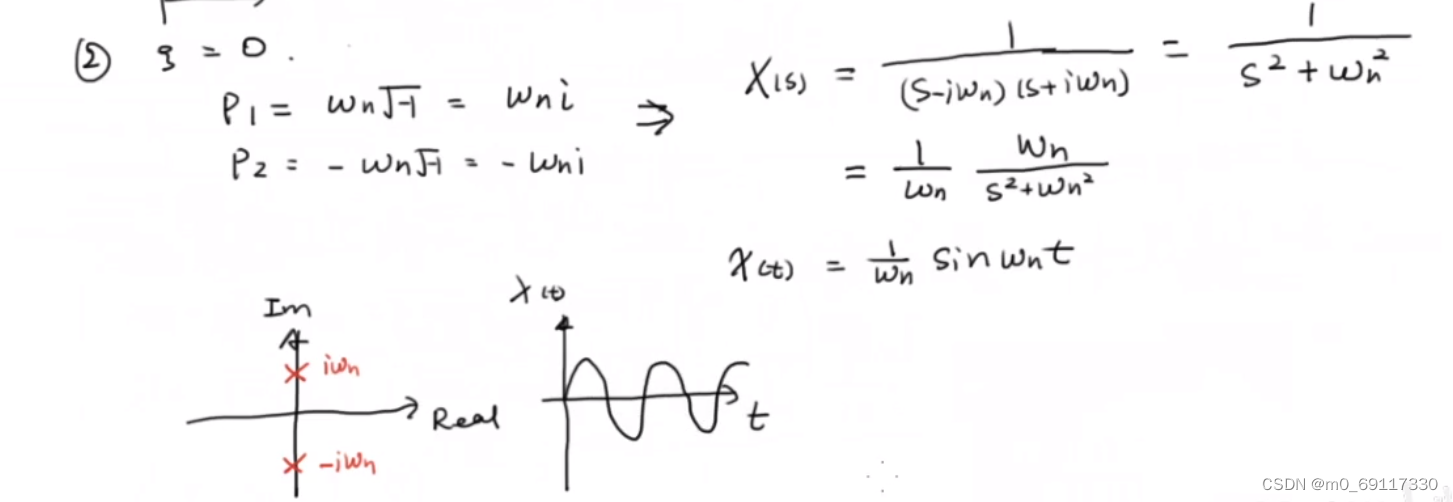

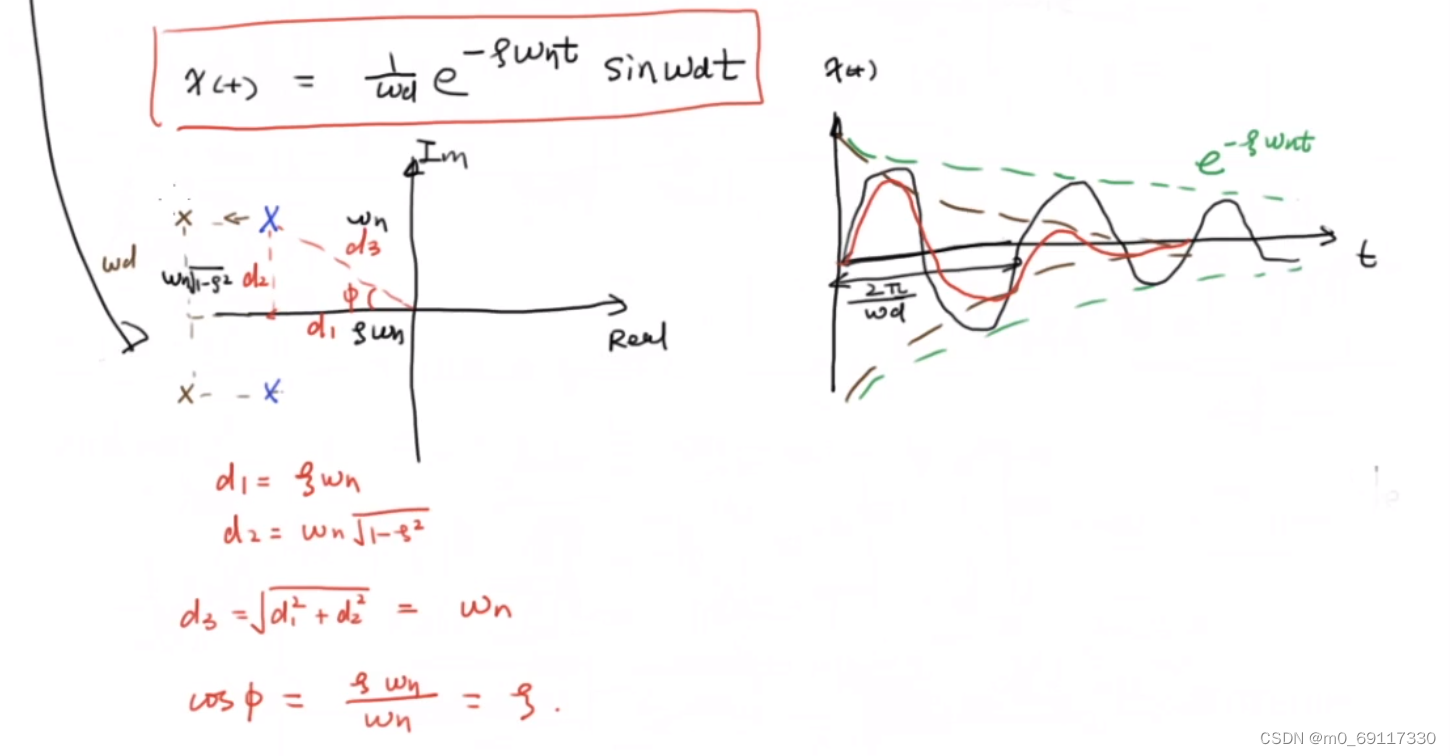
三阶系统:
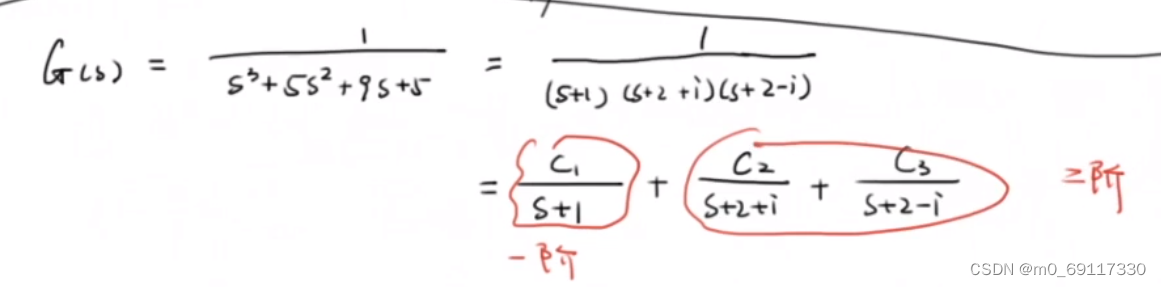
和一阶、二阶系统类似。
根轨迹的规则:
根轨迹的基本形式:
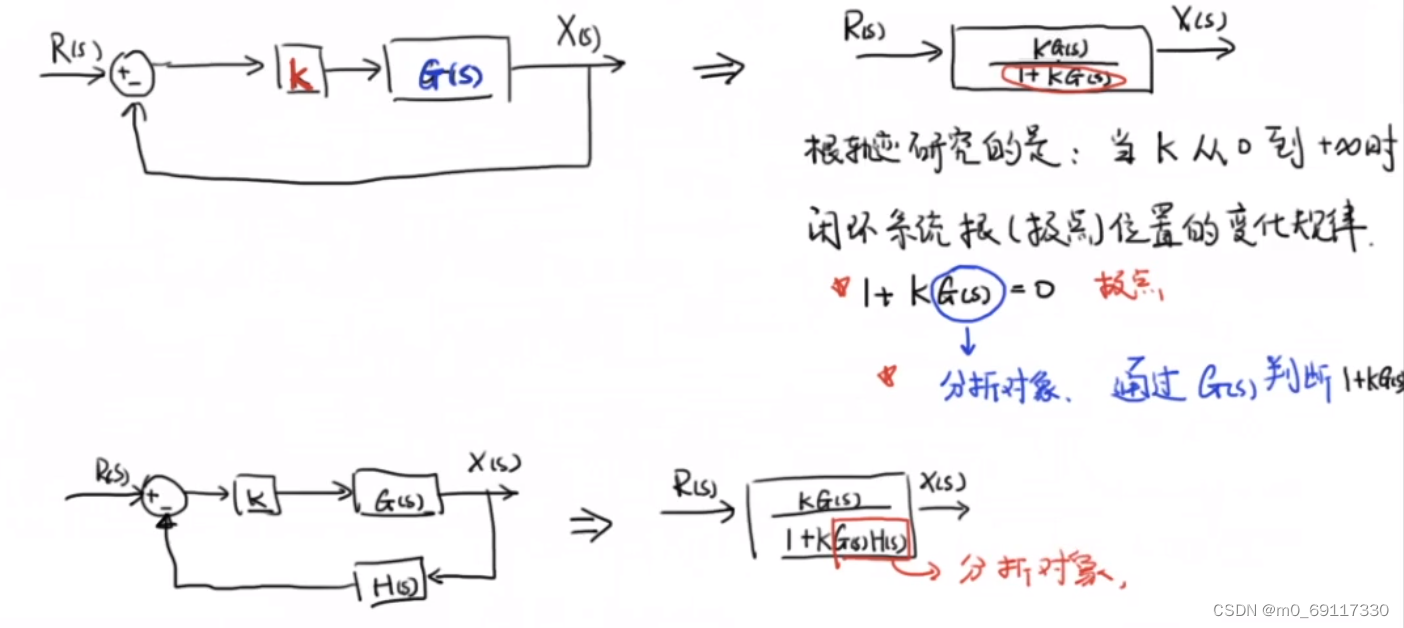
如果传递函数不是标准形式,则需要化为标准形式:
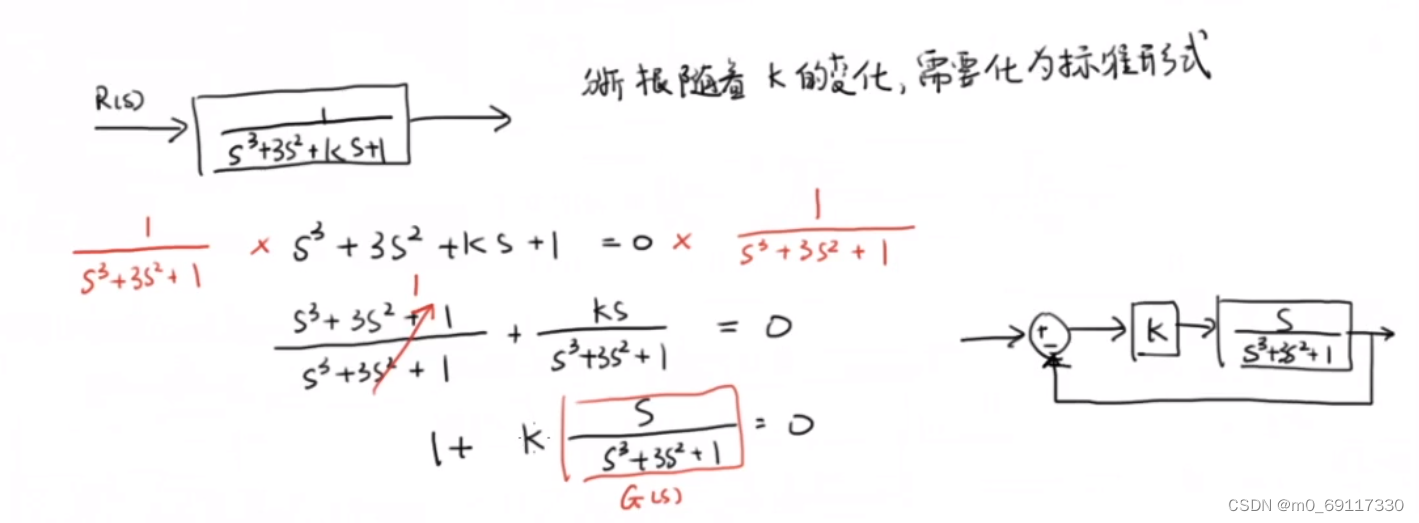
根轨迹的图像:

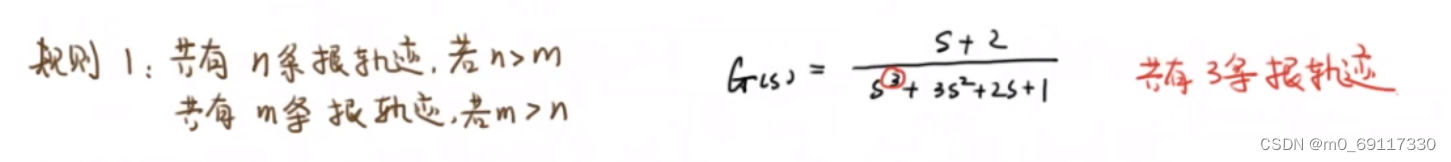
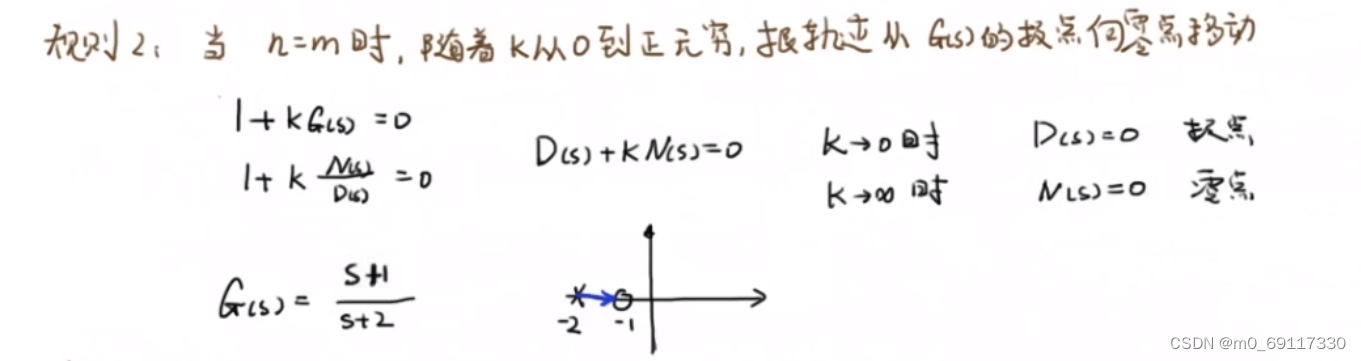




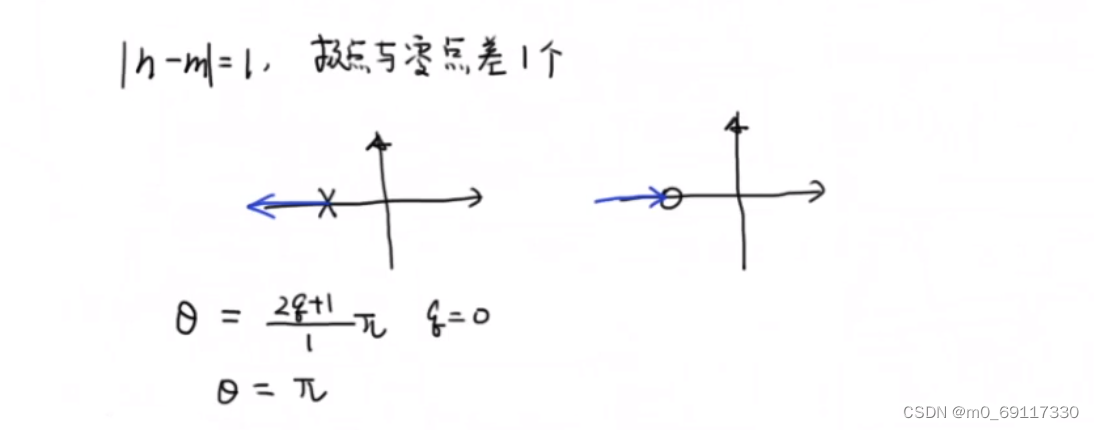

分离点/汇合点的求解:
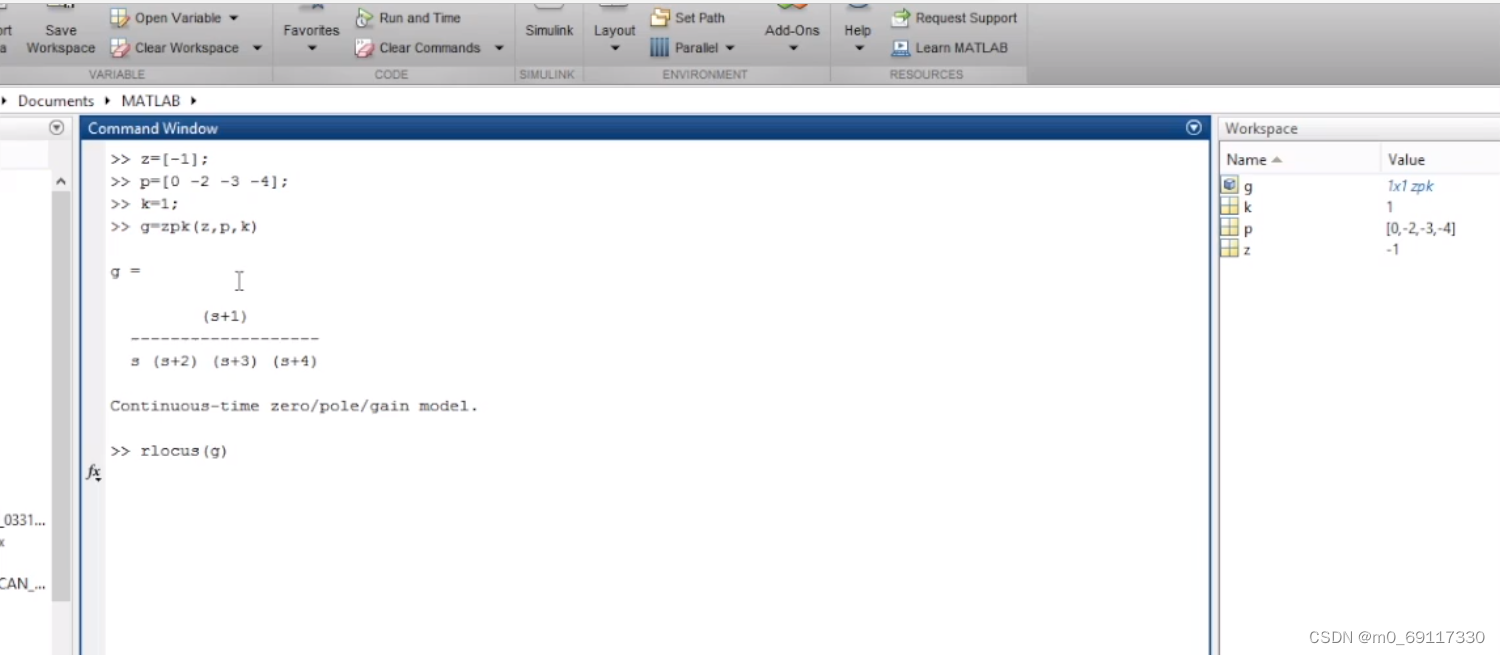
汇合点实例:
求极点和零点,并在复平面上画出大致的根轨迹
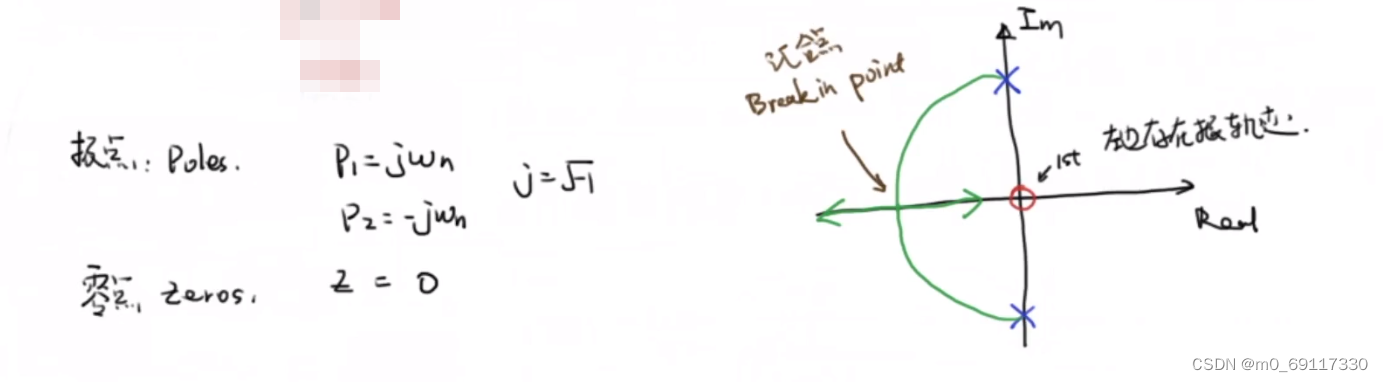
令传递函数的分母等于0,得:

既得到汇合点:

最终得到根轨迹:
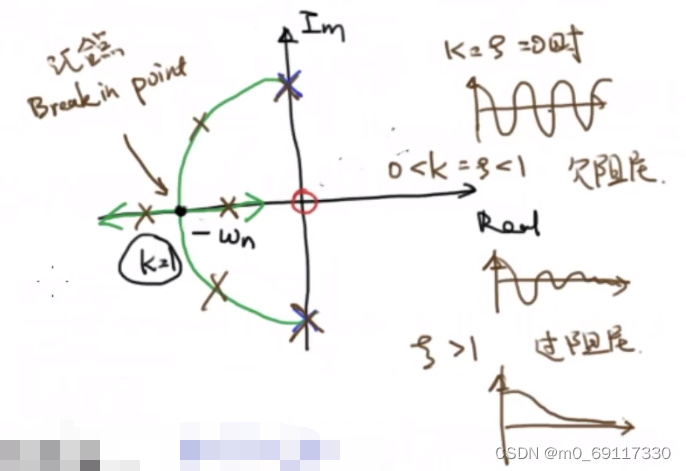
根轨迹的几何性质:
复数性质:

把一个复数带进传递函数:
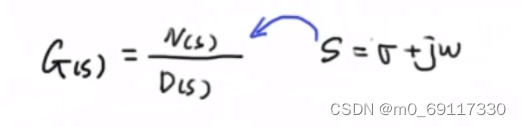
例如:
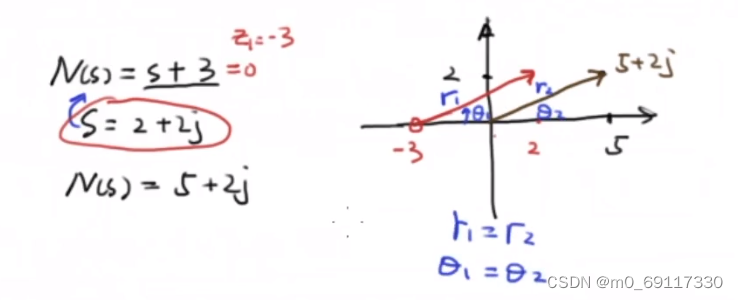
发现在求N(s)的模和夹角时,可以直接将N(s)=0的点与复数点连线,线段的长度既是N(s)的模,线段的夹角既是N(s)的夹角。
综上可得:

传递函数的模等于所有零点到这个复数长度的积除以所有极点到这个复数长度的积;
传递函数的夹角等于所有零点到这个复数的夹角的和减去所有极点到这个复数的夹角的和。
例一:
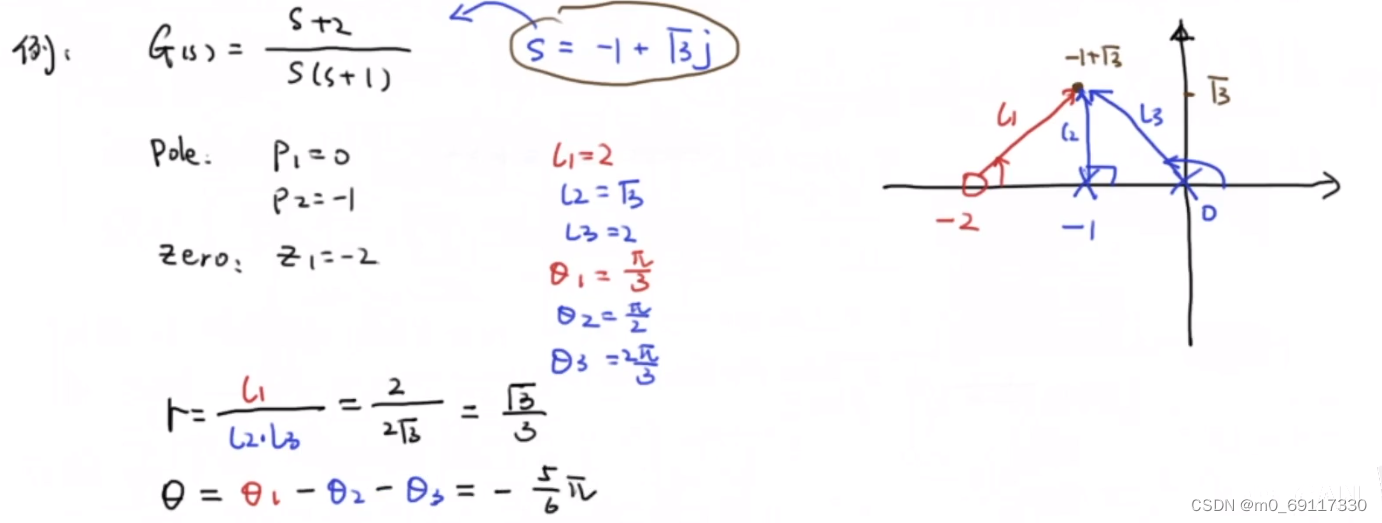
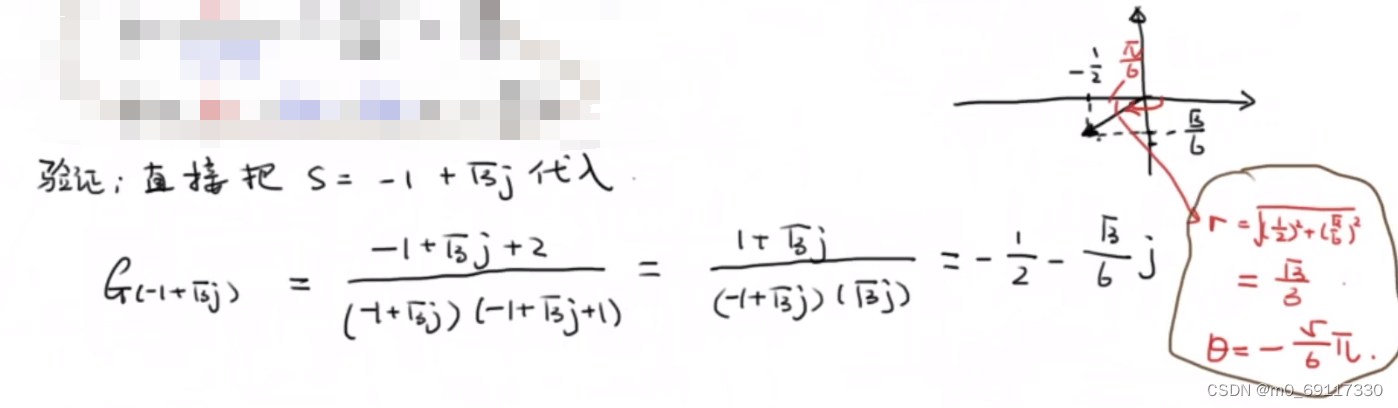
例二:
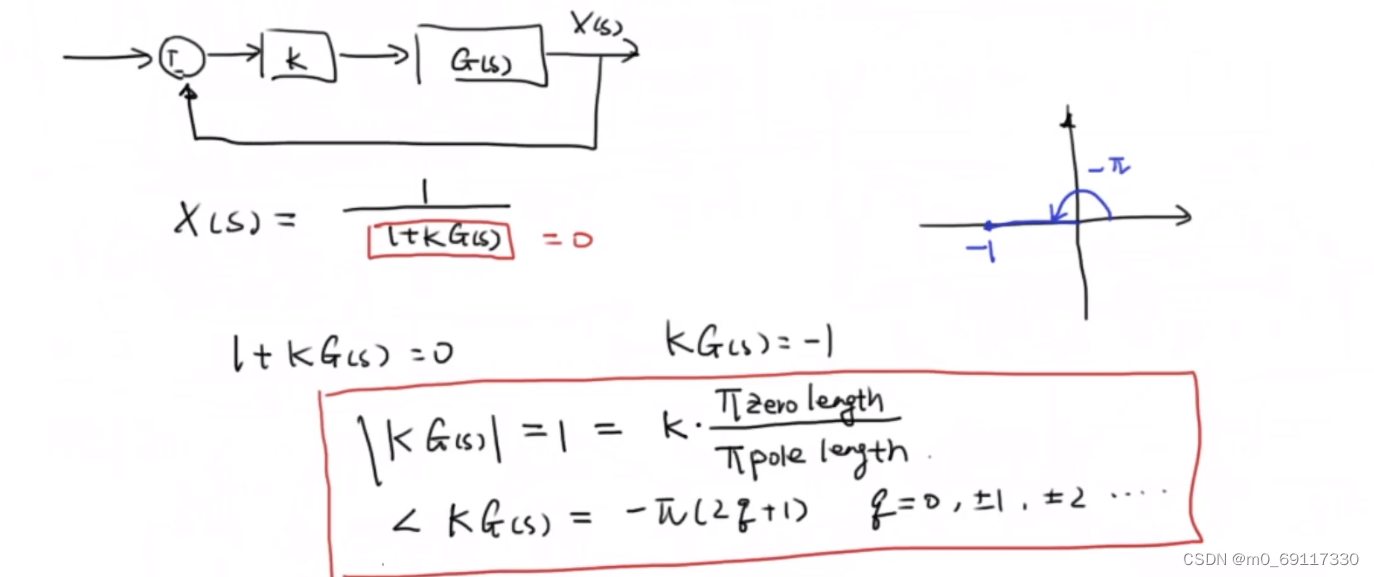
可以帮助我们判断一个根是否在根轨迹上,它必须要符合以上的条件。
频率响应:
振幅响应和相位响应:
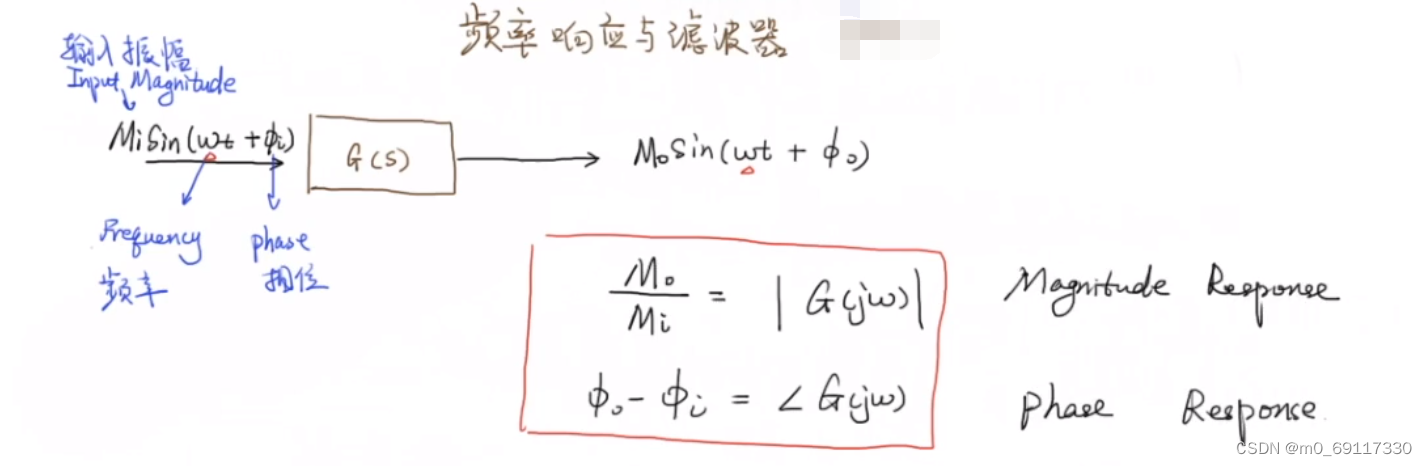
详细数学推导:
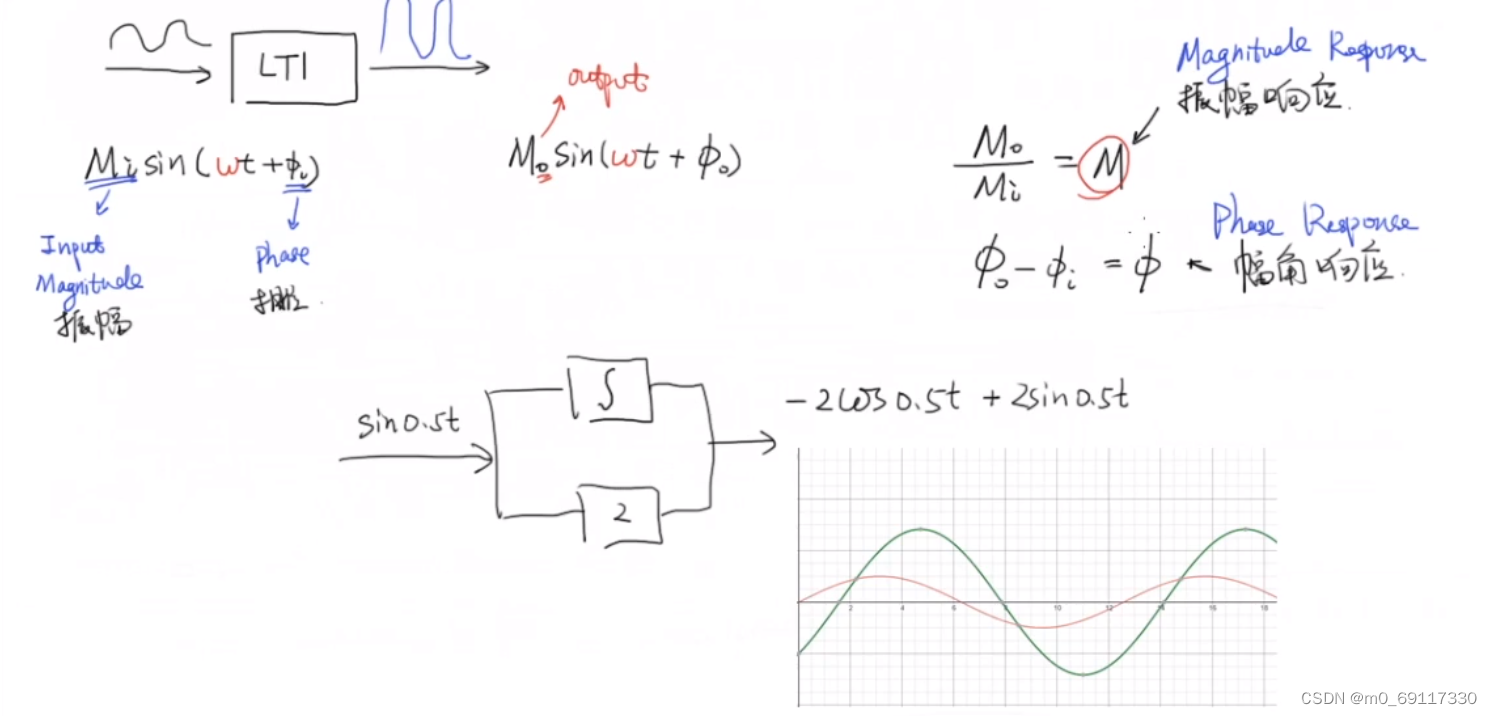
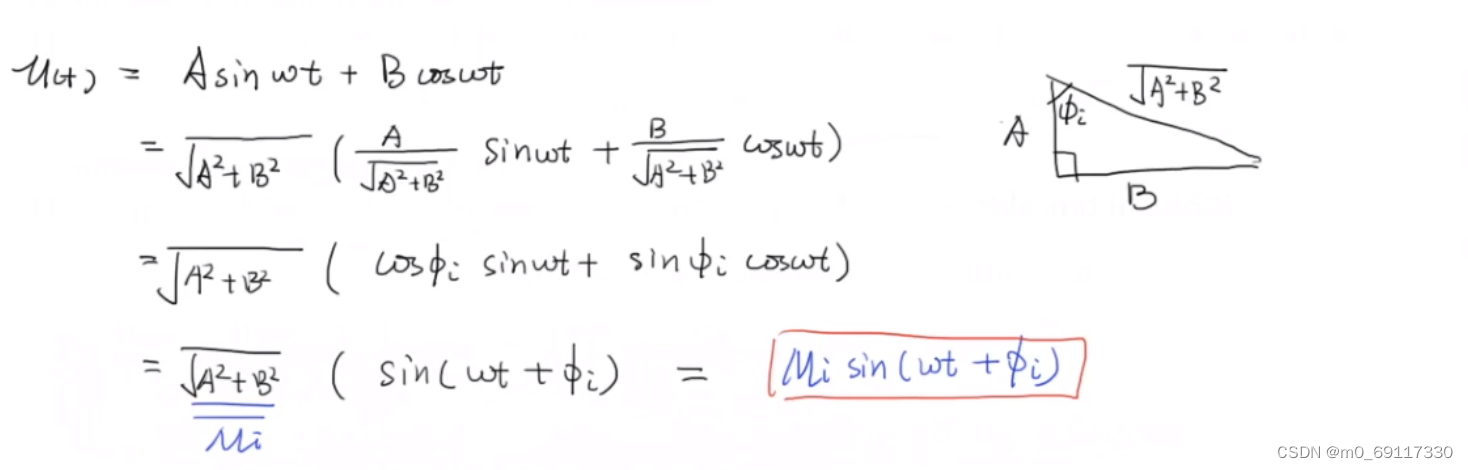
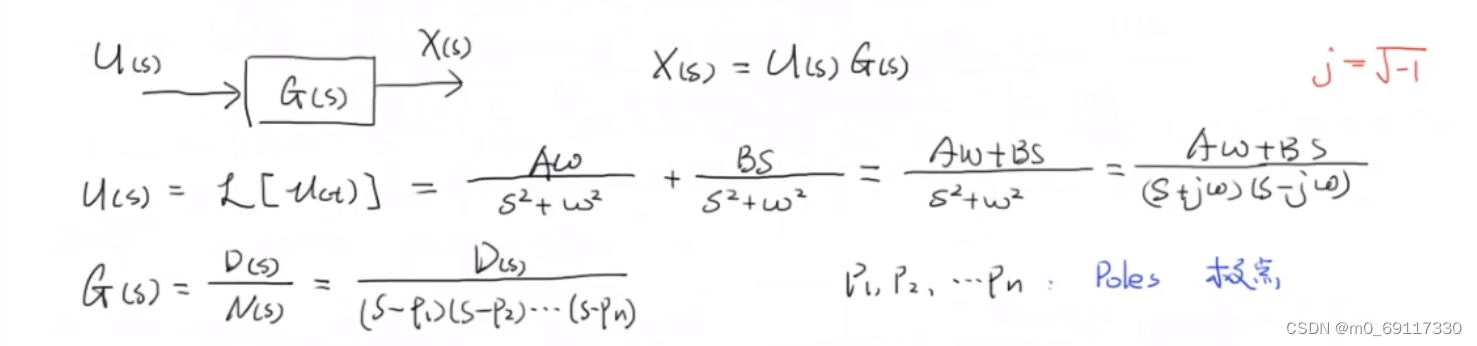




实例(低通滤波器):

一阶系统的频率响应实例:
低通滤波器:

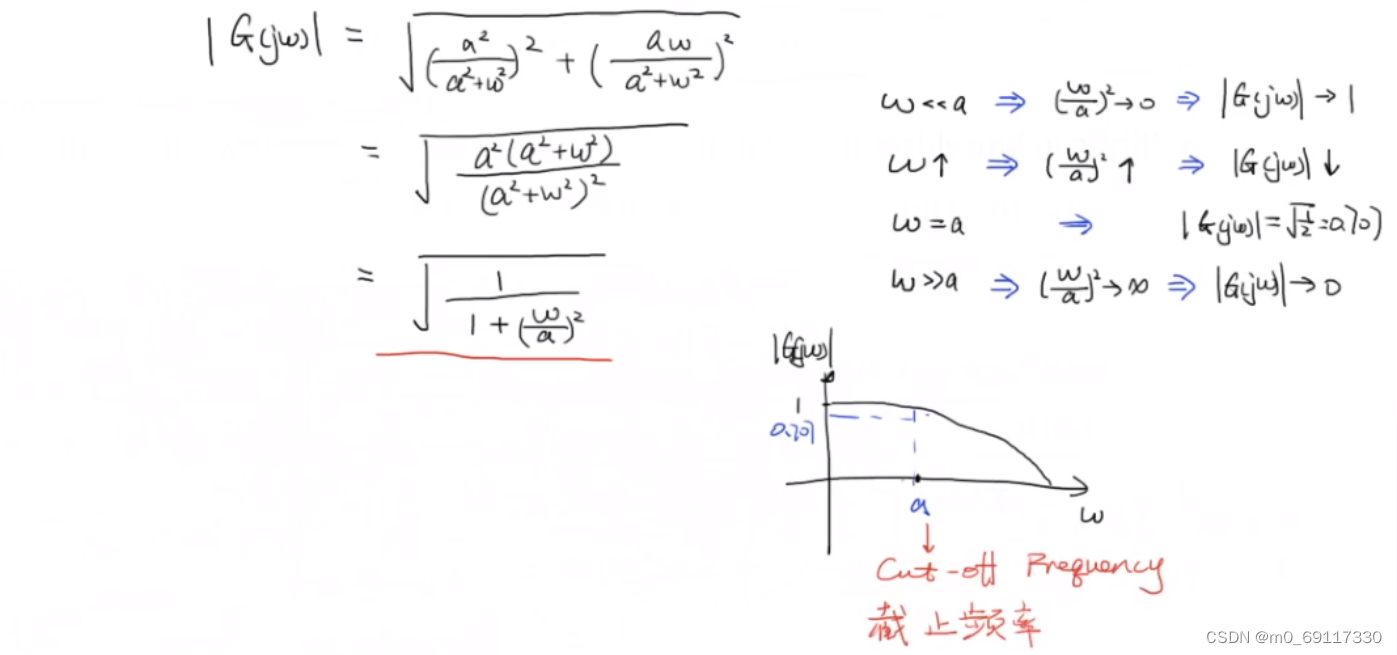
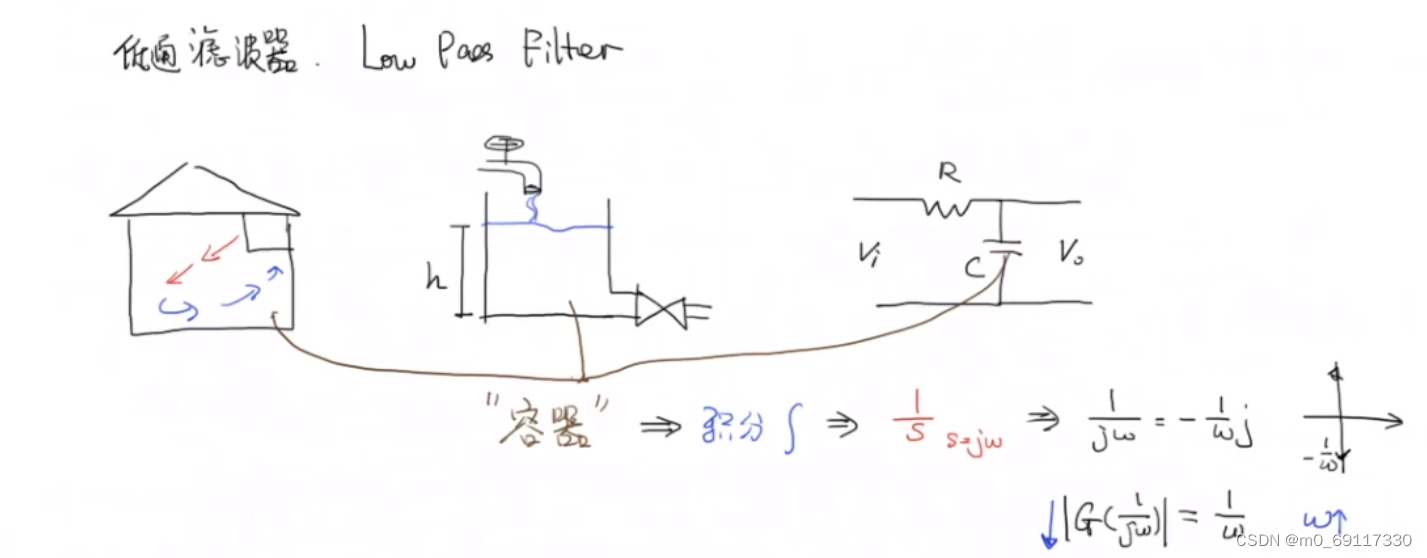
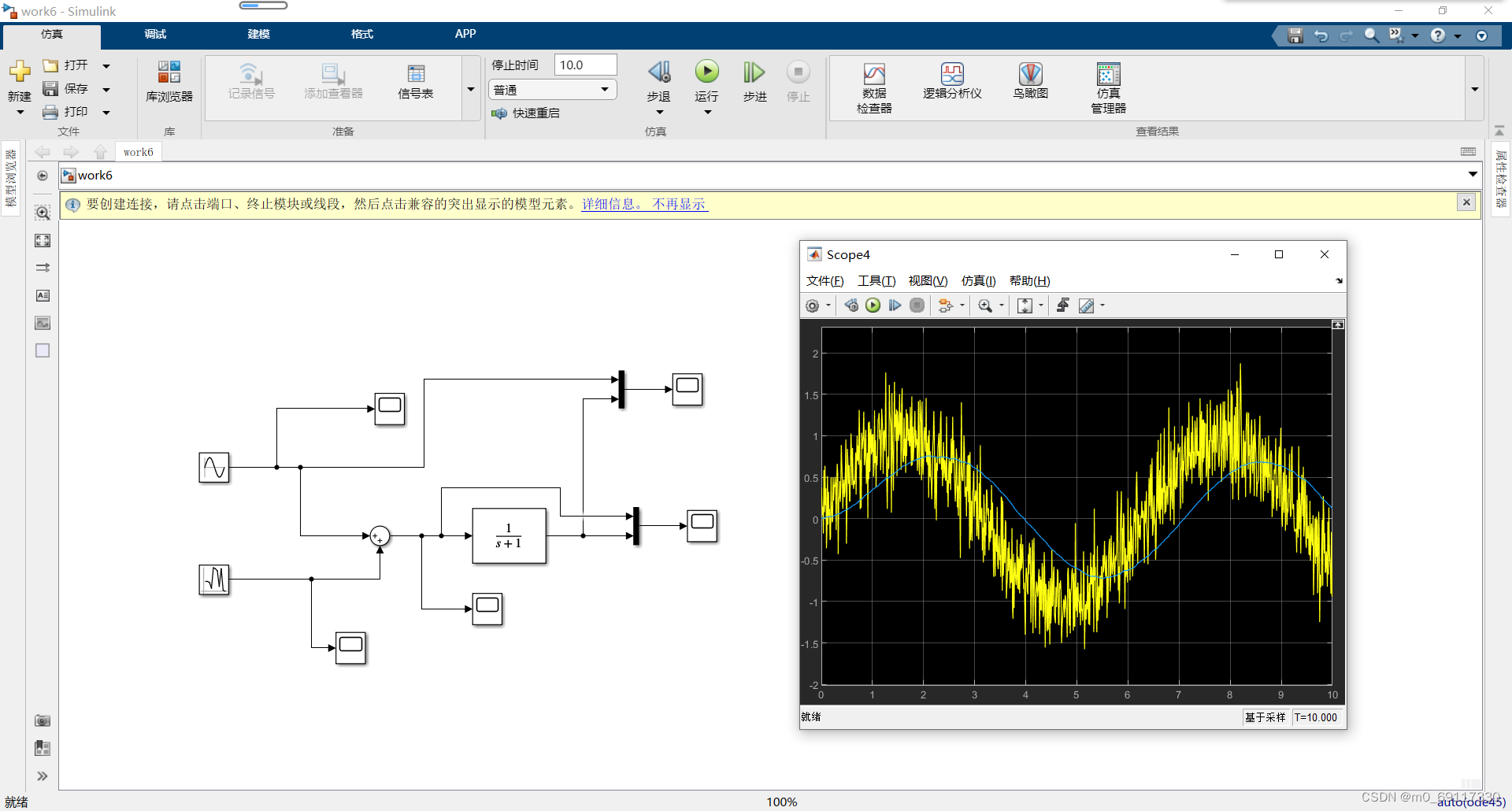
高通滤波器:
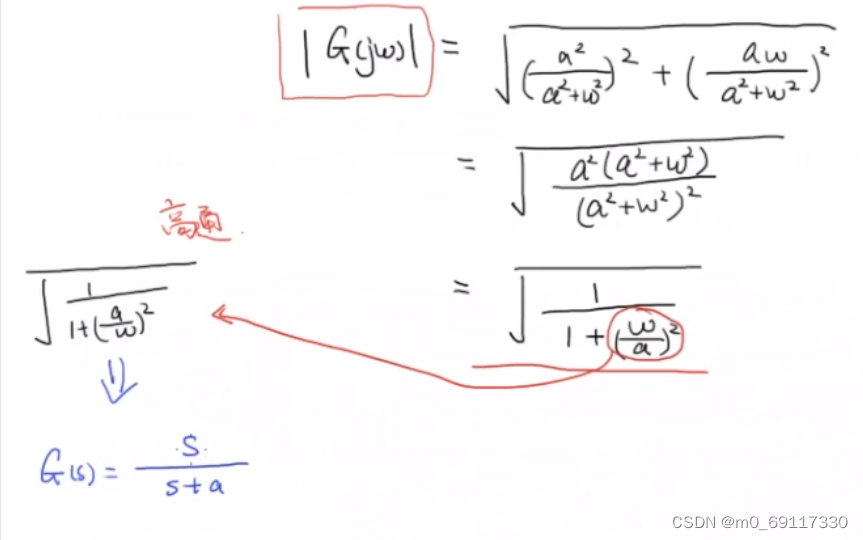
二阶系统的频率响应实例:

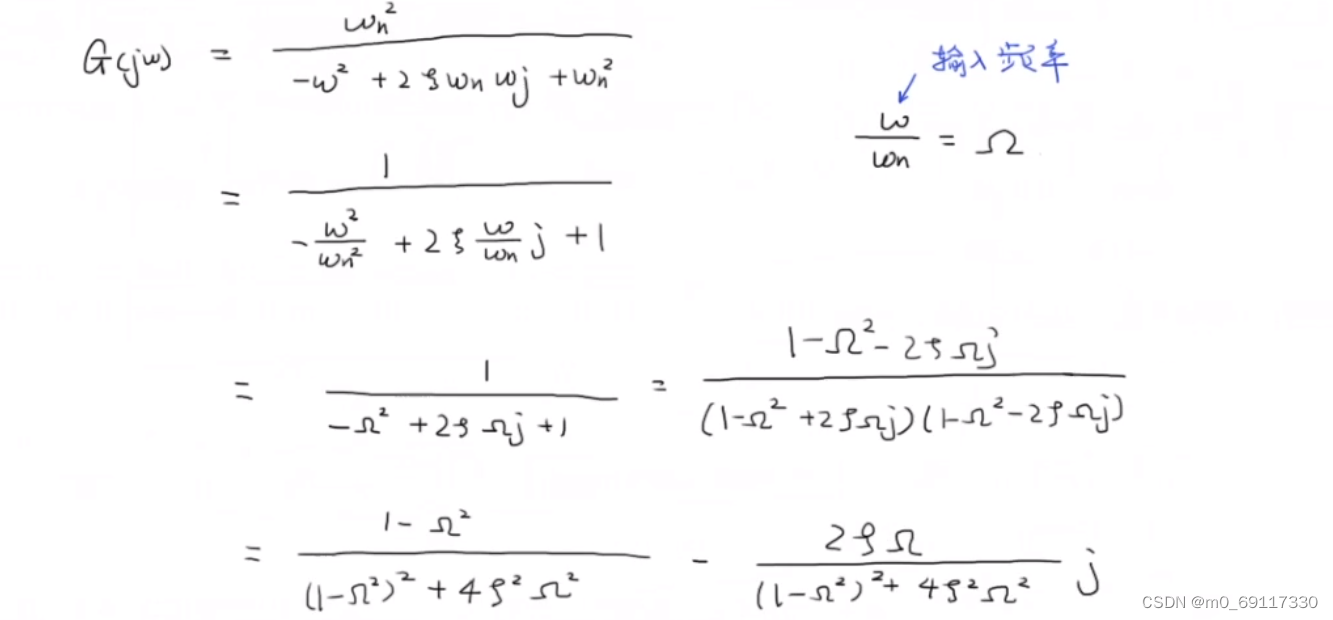


本文含有隐藏内容,请 开通VIP 后查看