定义:
二分查找也称折半查找(Binary Search),它是一种效率较高的查找方法。但是,折半查找要求线性表必须采用顺序存储结构,而且表中元素按关键字有序排列。它充分利用了元素间的次序关系,采用分治策略,可在最坏的情况下用O(log n)完成搜索任务。
它的基本思想是:(这里假设数组元素呈升序排列)将n个元素分成个数大致相同的两半,取a[n/2]与欲查找的x作比较,如果x=a[n/2]则找到x,算法终止;如 果x<a[n/2],则我们只要在数组a的左半部继续搜索x;如果x>a[n/2],则我们只要在数组a的右 半部继续搜索x。
1.二分查找
给出一个有序数对n(n=11):{1,2,3,6,9,10,11,13,15,16,20};求13的位置。
动画演示:二分查找与遍历查找的效率对比图
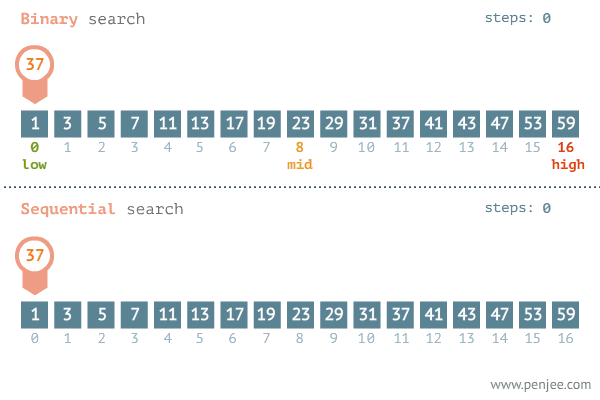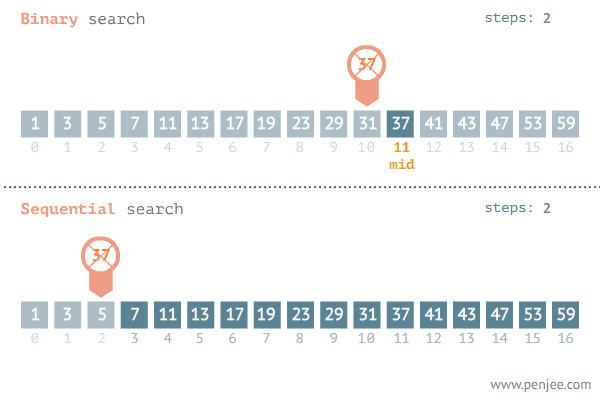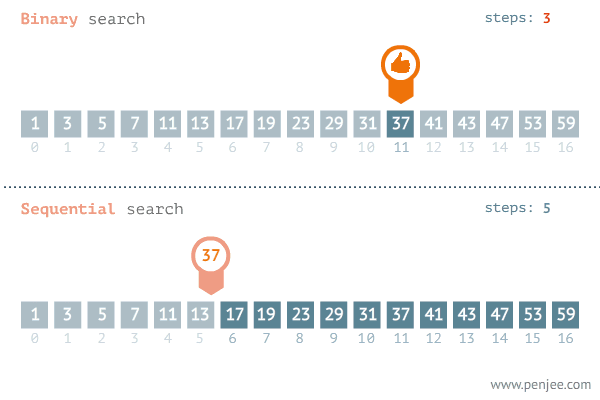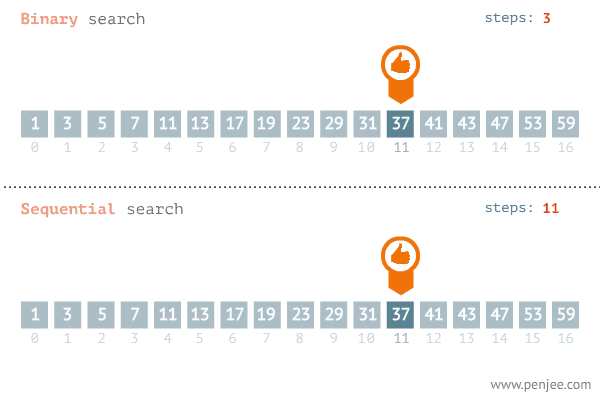
(1)朴素算法:枚举每一个数,从小到大的枚举,与数组进行匹配,最后找到x的位置i,输出。
时间复杂度:o(n);
(2) 二分法:因为是有序的,所以可以比较f[i]是否与x相等,比较大小,大的话则说明x的位置比当前i大,反之则小。
详细操作:设L=1,R=11,mid=(L+R)/2 ->中间值
①mid=6, f[mid](10)<13 , L=mid+1 说明13在右边,将L右移
②L=7,mid=7, f[mid](11)<13 ,L=mid+1
③L=8 mid=9, f[mid](15)>13,R=mid-1 说明十三在左边,R右移
④R=8,mid=8 f[mid](13)==13 return mid;
总结:刚刚操作中,不断将范围缩小一半,时间复杂度为 O(log n).
代码:
while(l<=r){
mid=(l+r)/2;
if(f[mid]==x) {cout<<mid;break;}
else if(f[mid]>x) r=mid-1;
else l=mid+1;
}2.二分答案
描述:类似于二分查找,题目中常常是把要求的答案进行二分,由起始的L,R不断判断mid值是否是全局的最优解,基于二分查找,只是多了判断mid可不可行。
模板(伪代码):
void check(int mid){
if( mid是可行解) return 1;
return 0;
}
while(l<=r){
mid=(l+r)/2;
if(check(mid)==1) l=mid+1;
else r=mid-1;
}题目练手:
SSOJ #4274. 「USACO 2021 US Open, Bronze」Acowdemia I
由于对计算机科学的热爱,以及有朝一日成为 「Bessie 博士」的诱惑,奶牛 Bessie 开始攻读计算机科学博士学位。经过一段时间的学术研究,她已经发表了 N篇论文,并且她的第 i 篇论文得到了来自其他研究文献的 ci次引用
Bessie 听说学术成就可以用 h 指数来衡量。h 指数等于使得研究员有至少 h 篇引用次数不少于 h 的论文的最大整数 h。例如,如果一名研究员有 4 篇论文,引用次数分别为 (1,100,2,3),则 h指数为 2,然而若引用次数为 (1,100,3,3)则 h 指数将会是 3。
为了提升她的 h 指数,Bessie 计划写一篇综述,并引用一些她曾经写过的论文。由于页数限制,她至多可以在这篇综述中引用 L篇论文,并且她只能引用每篇她的论文至多一次。
请帮助 Bessie 求出在写完这篇综述后她可以达到的最大 h指数。
分析:这道题目中让我们求最大的h值,即“至少 h 篇引用次数不少于 h 的论文的最大整数 h”,典型的二分题,用mid求h.
代码如下:
#include<bits/stdc++.h>
using namespace std;
int n,l1,c[10000010],l,r;
bool check(int mid){
int ans=0,l2=l1;
for(int i=n;i>=1;i--){//求出当h=mid时的ans
if(c[i]>=mid) ans++;
else if(l2>0&&c[i]+1==mid)ans++,l2--;
if(ans>=mid) return 1;//更新答案
}
return 0;
}
int main(){
cin>>n>>l1;
for(int i=1;i<=n;i++) cin>>c[i],r=max(r,c[i]+1);//求右端点
sort(c+1,c+n+1);//有序才能二分
while(l<=r){
int mid=(l+r)/2;
if(check(mid)) l=mid+1;//比答案小
else r=mid-1;//大
}
cout<<l-1;
return 0;
}总结:二分查找大大优化了搜索的范围,让我们高效的找到了全局的最优解。
再来一题:#2777. 河中跳房子 (house)
每年奶牛们都要举办各种特殊版本的跳房子比赛,包括在河里从一个岩石跳到另一个岩石。这项激动人心的活动在一条长长的笔直河道中进行,在起点和离起点 L 远 的终点处均有一个岩石。在起点和终点之间,有 N个岩石,每个岩石与起点的距离分别为 Di(0<Di<L)
在比赛过程中,奶牛轮流从起点出发,尝试到达终点,每一步只能从一个岩石跳到另一个岩石。当然,实力不济的奶牛是没有办法完成目标的。
农夫约翰为他的奶牛们感到自豪并且年年都观看了这项比赛。但随着时间的推移,看着其他农夫的胆小奶牛们在相距很近的岩石之间缓慢前行,他感到非常厌烦。他计划移走一些岩石,使得从起点到终点的过程中,最短的跳跃距离最长。他可以移走除起点和终点外的至多M(0≤M≤N) 个岩石。
请帮助约翰确定移走这些岩石后,最长可能的最短跳跃距离是多少?
分析:同样用mid表示“最长可能的最短跳跃距离”
代码:
#include<bits/stdc++.h>
using namespace std;
int s,n,d,l=1,r,mid,ans,a[50005];
int check(int x){
int j,q;j=q=0;
for(int i=1;i<=n+1;i++){
if(a[i]-a[j]<x) q++;
else j=i;
}
return q;//求移走后的最长距离
}
int main(){
cin>>s>>n>>d;
for(int i=1;i<=n;i++) cin>>a[i];
sort(a+1,a+n+1);//排序
l=1,r=s;
a[n+1]=s;//终点是最后一块石头
while(l<=r){
mid=l+(r-l)/2;//重点!!!
if(check(mid)<=d) ans=mid,l=mid+1;//左
else r=mid-1;//右
}
cout<<ans<<endl;
}三.二分的缺陷
① 必须有序,很难保证数组都是有序的。当然可以在构建数组的时候进行排序,可是又落到了第二个瓶颈上:它必须是数组。数组读取效率是O(1),可是它的插入和删除某个元素的效率却是O(n)。因而导致构建有序数组变成低效的事情。
② 数据量太小,太大,都不适合二分。
小:如果要处理的数据量很小,完全没有必要用二分查找,顺序遍历就足够了。比如我们在一个大小为 10 的数组中查找一个元素,不管用二分查找还是顺序遍历,查找速度都差不多,只有数据量比较大的时候,二分查找的优势才会比较明显。
大:二分查找底层依赖的是数组,数组需要的是一段连续的存储空间,所以我们的数据比较大时,比如1GB,这时候可能不太适合使用二分查找,因为我们的内存都是离散的,可能电脑没有这么多的内存。