概述

PID属于一种负反馈控制方法,也被叫做闭环控制

实现很简单,成本较低,使用非常广泛(可以使用阻容器件配合运放实现)

当然本文是数字信号控制,使用单片机

PID控制的目标是将当前的值稳定在一个设定的范围内

比如热水器的温度控制等等

原理

逻辑

PID是反馈控制

反馈指的是将输出量以一个规则去影响输入,让输入去改变输出

PID有三个控制单元,分别是比例(P)积分(I)微分(D),逻辑框图如下

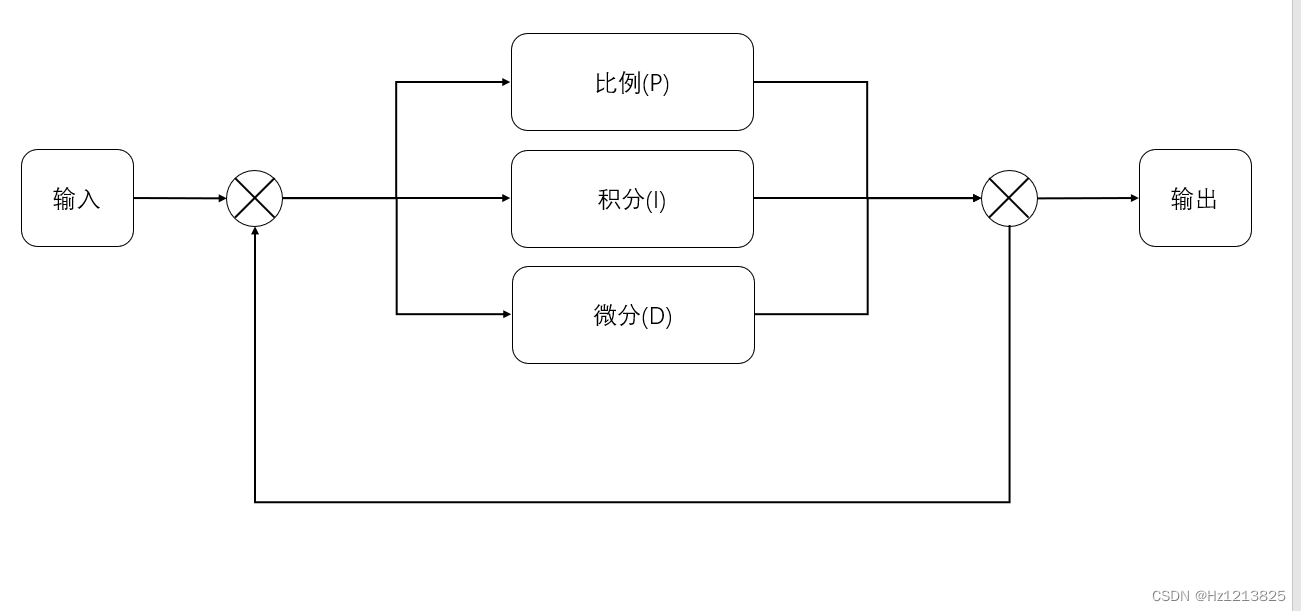
输入的有两方面的数值

1.是设定的值

2.是输出状态送来的反馈的值

输出的一定是影响输入的量,设计的时候别出现输出和输入完全独立,听起来像是废话,但有很多人在这里犯迷糊

比例(P)

我们想象一个简单的模型来理解这里

读者应该都学过物理吧,我们来想象一个很简单场景

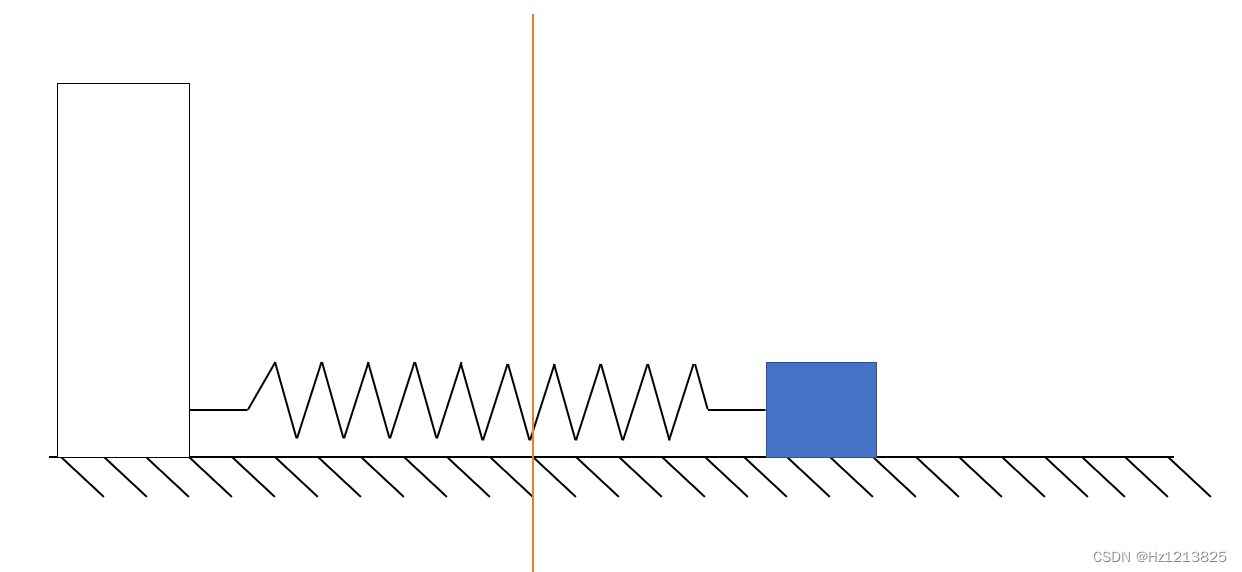
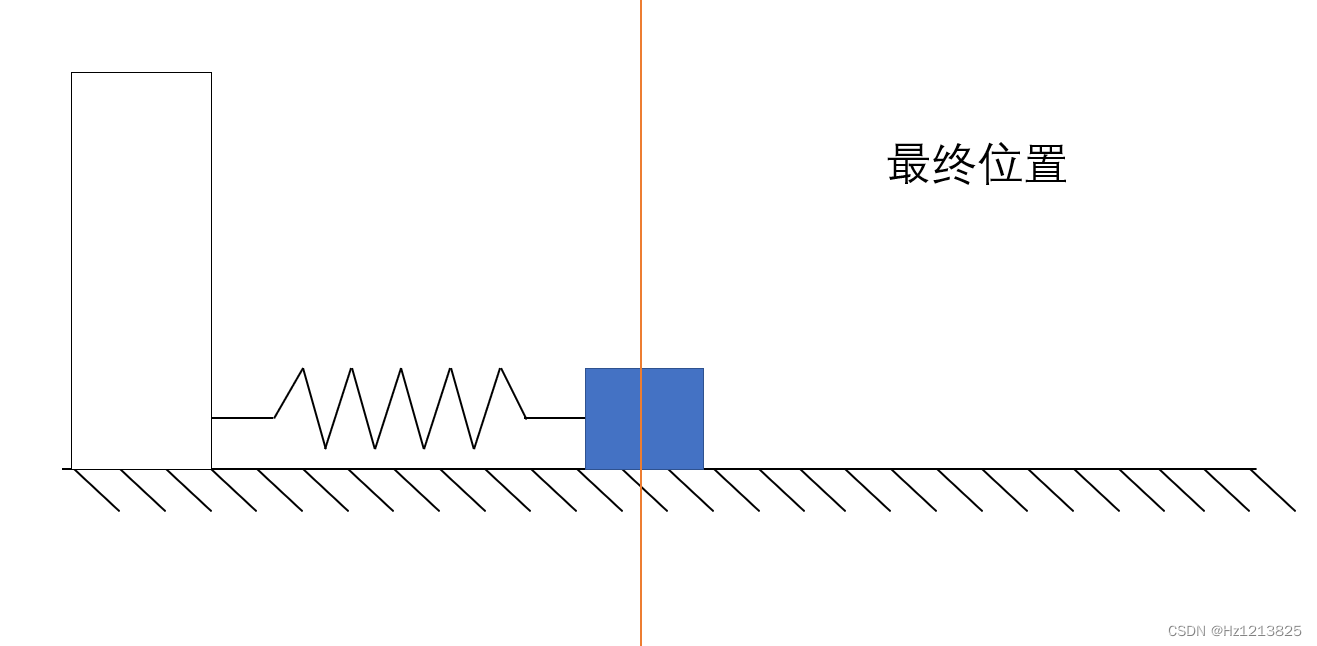
在地面上,水平放置一个弹簧和滑块,弹簧的原长位置为红线处,释放滑块(如下图1)

因为摩擦力的关系,滑块并不会停留在原长位置,它可能会停在静摩擦力(干扰)与弹簧弹力平衡的点

在这个例子里,弹簧是我们的控制系统,它产生的力的大小与距离成正比,方向时刻指向原长的位置

原长(红线)处是设定的目标值,这就是比例控制

比例控制就是将目标值和当前值之间的差值(误差) (存在正负,正代表当前值小于目标值)乘上一个系数之后作为控制的一部分

比例控制是自然现象里非常常见的,本质上就是给被控对象一个达到目标值的动力

目标值和当前值距离越远,给一个越大的动力,可以让其更快的达到目标值(这就是为什么不给一个恒定的动力)

方向特别重要,动力的方向必须得时刻指向目标值

这里的动力在不同的控制中不同,在例子里是力,在温度控制里是加热和制冷(并不一定是物理上的力)

单独使用比例控制被控对象往往不会达到目标值

这是因为在现实环境里存在干扰,当这个干扰在某个点与动力相等时,当前值便不会更进一步接近目标值了(这个误差被称为稳态误差)

积分(I)

那要怎么更改我们的控制系统(如上例中的弹簧),才能让当前值在误差范围内与目标值相等呢?

我们可以引入误差的累积,如果比例控制因为干扰导致出现在目标值之外的点停下来,误差的累积则会一直增加(绝对值增大)

那这个累积则会作为比例控制之外的动力进一步推动当前值接近目标值

这部分的方向和比例部分的方向相同，并不需要特别设置

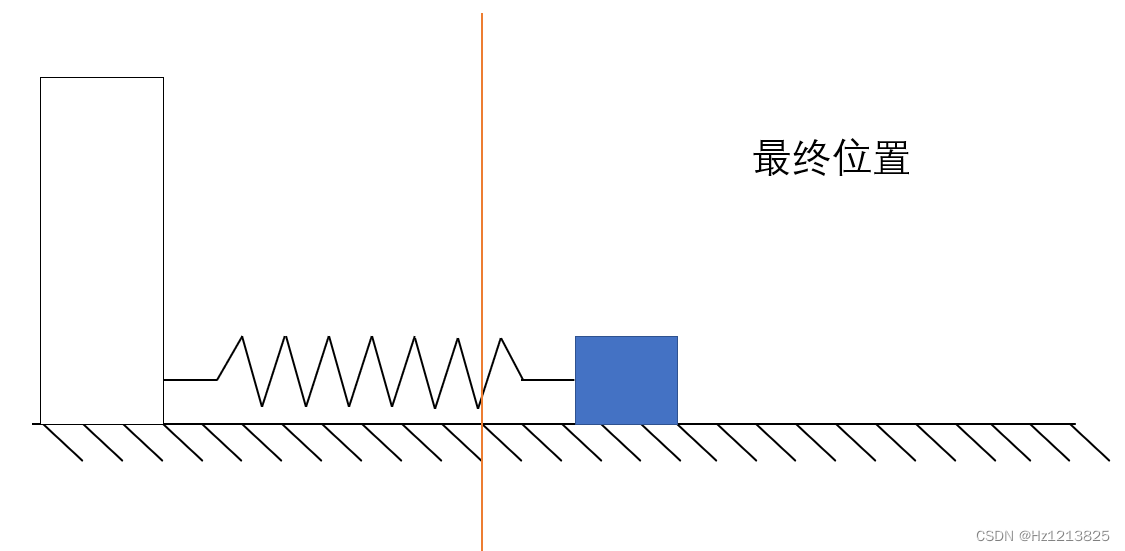
回到上文提到的例子

这次的弹簧变成了一个可以自由变动弹力的装置(还用弹簧表示)

在这个误差的累积的推动作用下,滑块可以来到原长处(目标点)

所以我们的算法迭代到了第二个版本

首先是比例控制部分,每时每刻根据当前值与目标值的偏差来提供动力

其次是积分控制部分,每时每刻根据从系统运行到现在的误差的累积来作为弥补稳态误差的第二动力

因为现实中的系统是连续的状态

每时每刻的累积(求和)就是积分

因此积分部分就变成了对误差函数从0到此时刻的定积分,即

$gif.latex?%5Cint_%7B0%7D%5E%7Bt%7De%28t%29%29dt$

e(t)是误差函数,表示 t 时刻的误差

PID算法到了这里,已经可以达到控制的目标了(将当前的值稳定在一个设定的范围内)

微分(D)

微分部分则是用来优化整个控制算法的

之前的算法有什么问题呢?

如果比例和微分控制部分的系数较大,则会让误差出现过冲(即每次通过目标值会产生较大的偏差)而这两个系数又不能过小

下图中横轴是时间,纵轴是当前值,虚线是目标值

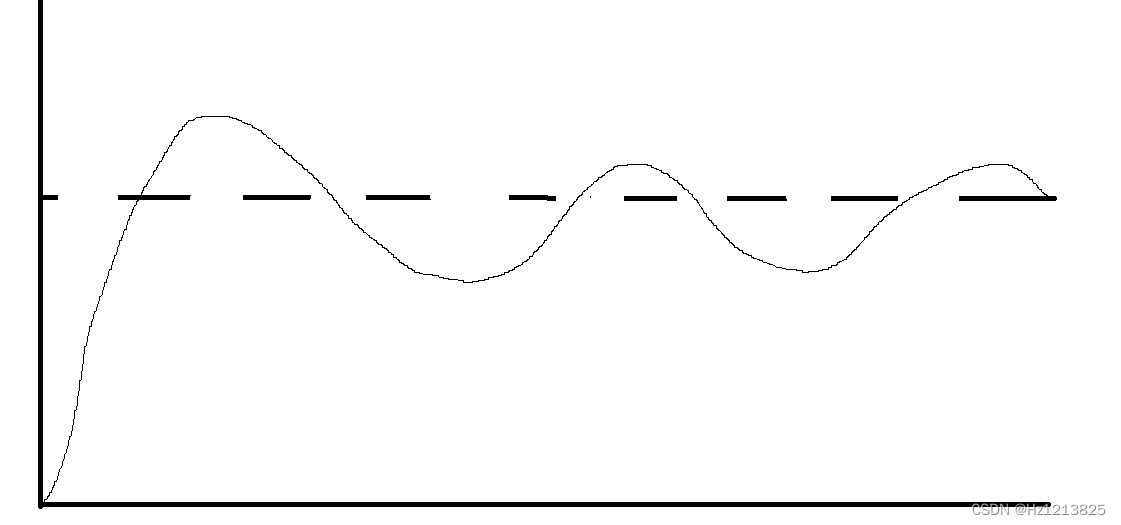
而微分部分就是用于改善这个现象的

微分又叫求导,求出的数值是函数在这点的变化率(高数)

那现在问题就简单了,只需要对当前的误差函数 e(t) 进行求导,之后乘上一个系数作为控制的一部分即可了

它永远阻碍误差的变化趋势，也就是让误差变的过冲减少

如下图分析，在开始的阶段，误差(目标值-当前值)从正快速下降，微分项为-(积分和比例项均为+)使变化速率降低，减少过冲，依次类推

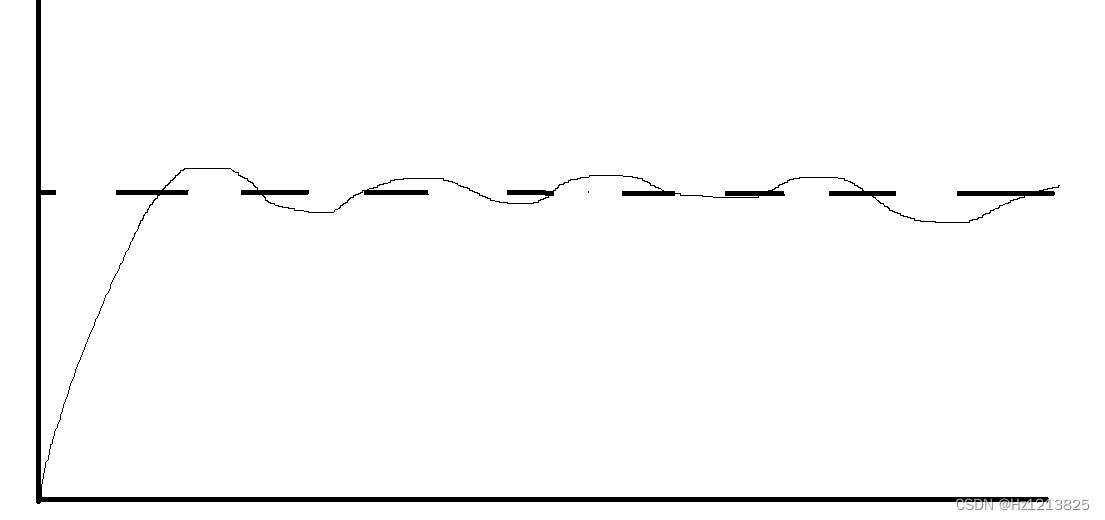
加上微分部分则会使其变得更加丝滑(抖动变得更小)

PID公式

经过上文介绍我们已经明白PID控制的原理,到了现在我们就需要实现PID了

连续态公式

$gif.latex?%5Cdpi%7B200%7D%20u%28t%29%3DK_%7Bp%7D%5Ctimes%20e%28t%29+K_%7Bi%7D%5Ctimes%20%5Cint_%7B0%7D%5E%7Bt%7De%28t%29dt+K_%7Bd%7D%5Ctimes%20%5Cfrac%7Bde%28t%29%7D%7Bdt%7D$

u(t)--->输出函数,经过PID计算后的输出,给到输出机构

$gif.latex?%5Cdpi%7B120%7D%20K_%7Bp%7D%2CK_%7Bi%7D%2CK_%7Bd%7D$ ----->系数

e(t)---->误差值(目标值-当前值)

在模拟电路里实现就是使用的这个公式

离散态公式

数字电路只能处理离散的数据,因此需要将连续态公式进行离散化

位置式

有高数知识的应该知道,积分就是累加求和,微分就是求当前的变化率

将其根据时间离散化,即每隔一段时间(几ms)进行一次PID运算求出u(t)的值

那比例部分自然不需要改变(只与位置有关,和时间并无关系)

积分部分,即系统运行到现在时刻所有误差的求和(每几ms计算一次误差) $\sum_{i=0}^{k}e(i)$

微分部分, 这次运算与上次运算的所连成直线(e-t图相)的斜率 $\frac{e(k)-e(k-1)}{\Delta t}$

而 $\Delta t$ 在此运算中是常数,间隔固定时间调用,因此可以将其合到系数 $K_d$ 里

$u(k)=K_p\times e(k)+K_i\times \sum_{i=0}^{k}e(i)+K_d\times \left \{ e(k)-e(k-1) \right \}$

所以离散位置式PID的公式就是如上

u(k)是直接输出给执行机构的

e(k)是k次调用的误差(目标值-当前值)

增量式

位置式看起来很完美了(事实上也是如此),但还有一个问题:

如果在环境变化剧烈或者需要长时间稳定运行的情况下,误差的累积这个数值将会一直增加,而计算机中是数都是存在上限(范围)的,这样可能会出现某些问题

那该怎么办呢?

我们可以计算 $\Delta u=u(k)-u(k-1)$ ,

之前的计算的结果被放入了输出值里了,

可以使用 $u(k)=u(k-1)+\Delta u$ 来计算输出机构的值

这样只需要存下的数据并不会一直增大到超出范围的地步

$\Delta u(k)=K_p\times \left \{ e(k)-e(k-1) \right \}+K_i\times e(k)+K_d\times \left \{ e(k)-2\times e(k-1)+e(k-2) \right \}$

$u(k)=u(k-1)+\Delta u(k)$

PID实现

位置式

先分析一波

对于函数来说需要存下来的数据(全局变量)有 $K_p,K_i,K_d,e(k-1),Integral$ (积分值)

每调用一次PID函数需要传入的值(局部变量)有,Target(目标值),Current(当前值)

我们先建立一个结构体,将需要的全局变量放进去,并建立此结构体的全局变量

typedef struct __PID_Position_Struct
{
  float Kp, Ki, Kd;     //系数
  float Integral;    //积分(累积)
  float Error_Last1; //上次误差
} PID_Position_Struct;

PID_Position_Struct PID = {0};

每隔固定的时间进行一次PID计算

/**
 * @brief 位置式PID计算
 * @param PID:PID结构体
 * @param Current:当前值
 * @param Target:目标值
 * @return 输出
 * @author HZ12138
 * @date 2022-08-05 13:07:23
 */
float PID_Position(PID_Position_Struct *PID, float Current, float Target)
{
  float err,                                                                                                        //误差
      out,                                                                                                          //输出
      differential;                                                                                                 //微分
  err = (float)Target - (float)Current;                                                                             //计算误差
  PID->Integral += err;                                                                                             //更新积分
  differential = (float)err - (float)PID->Error_Last1;                                                              //计算微分
  out = (float)PID->Kp * (float)err + (float)PID->Ki * (float)PID->Integral + (float)PID->Kd * (float)differential; //计算PID
  PID->Error_Last1 = err;                                                                                           //更新误差
  return out;
}

增量式

依旧先分析一波

对于函数来说需要存下来的数据(全局变量)有 $K_p,K_i,K_d,e(k-1),e(k-2),out$ (上次输出)

每调用一次PID函数需要传入的值(局部变量)有,Target(目标值),Current(当前值)

我们先建立一个结构体,将需要的全局变量放进去,并建立此结构体的全局变量

typedef struct __PID_Increment_Struct
{
  float Kp, Ki, Kd;  //系数
  float Error_Last1; //上次误差
  float Error_Last2; //上次误差
  float Out_Last;    //上次输出
} PID_Increment_Struct;

PID_Increment_Struct PID = {0};

每隔固定的时间进行一次PID计算

/**
 * @brief 增量式PID计算
 * @param PID:PID结构体
 * @param Current:当前值
 * @param Target:目标值
 * @return 输出
 * @author HZ12138
 * @date 2022-08-05 13:20:36
 */
float PID_Increment(PID_Increment_Struct *PID, float Current, float Target)
{
  float err,                                                                                                       //误差
      out,                                                                                                         //输出
      proportion,                                                                                                  //比例
      differential;                                                                                                //微分
  err = (float)Target - (float)Current;                                                                            //计算误差
  proportion = (float)err - (float)PID->Error_Last1;                                                               //计算比例项
  differential = (float)err - 2 * (float)PID->Error_Last1 + (float)PID->Error_Last2;                               //计算微分项
  out = (float)PID->Out_Last + (float)PID->Kp * proportion + (float)PID->Ki * err + (float)PID->Kd * differential; //计算PID
  PID->Error_Last2 = PID->Error_Last1;                                                                             //更新上上次误差
  PID->Error_Last1 = err;                                                                                          //更新误差
  PID->Out_Last = out;                                                                                             //更新上此输出
  return out;
}

PID级联

级联一般有两种目的

1.有多个预期的控制内容(如热水器例子,水面保持位置和温度保持)

2.提高控制收敛速度(如电机控制加入电流PID)

串级PID

上一级的输出作为下一级的输入

如使用角度环和速度环控制电机位置的系统

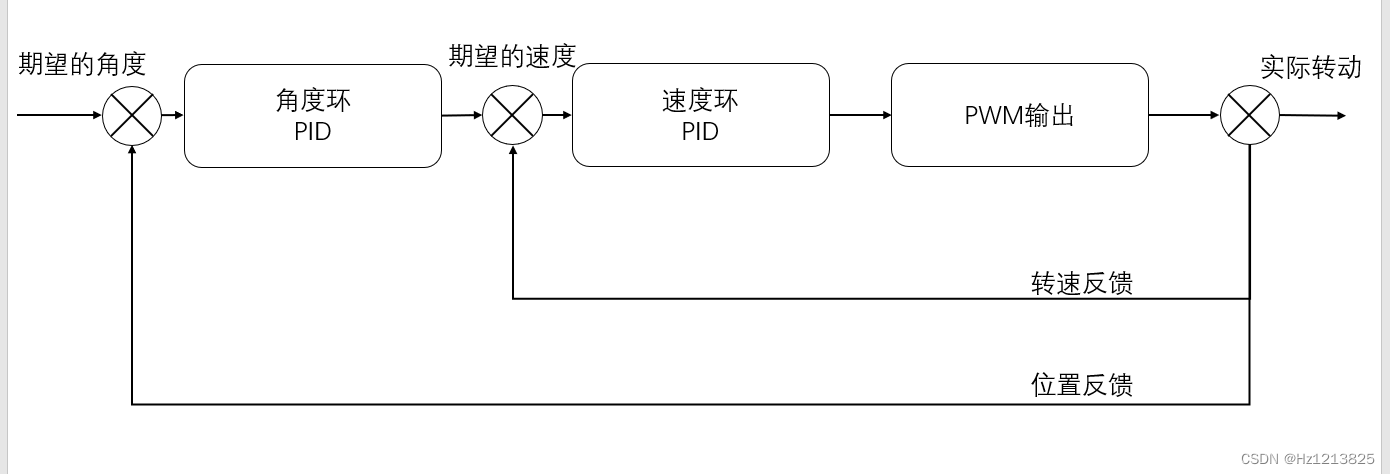
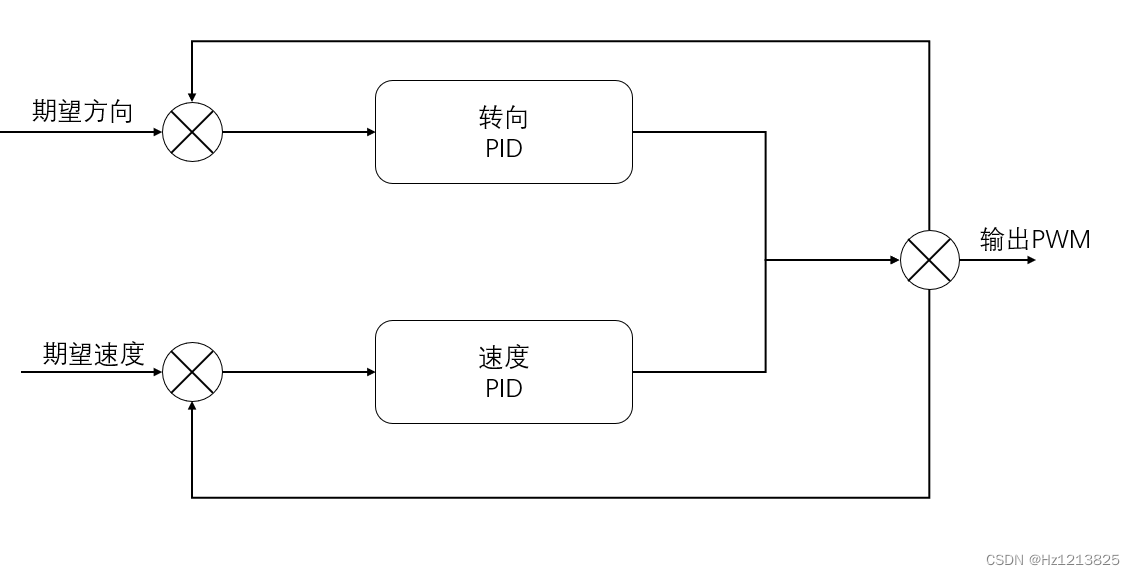
并级PID

有多个期望输入,输出同时叠加到一起

本文含有隐藏内容，请开通VIP 后查看

【基础知识】PID(比例微分积分)控制

概述

原理

逻辑