目录
LeetCode235. 二叉搜索树的最近公共祖先
链接: 235. 二叉搜索树的最近公共祖先 - 力扣(LeetCode)
1. 思路
做过二叉树的最近公共祖先题目的同学应该知道,利用回溯从底向上搜索,遇到一个节点的左子树里有p,右子树里有q,那么当前节点就是最近公共祖先。那么本题是二叉搜索树,二叉搜索树是有序的,那得好好利用一下这个特点。
在有序树里,如果判断一个节点的左子树里有p,右子树里有q呢?
其实只要从上到下遍历的时候,cur节点是数值在[p, q]区间中则说明该节点cur就是最近公共祖先了;理解这一点,本题就很好解了。
为什么是最近的呢?会不会是次近的?Example:
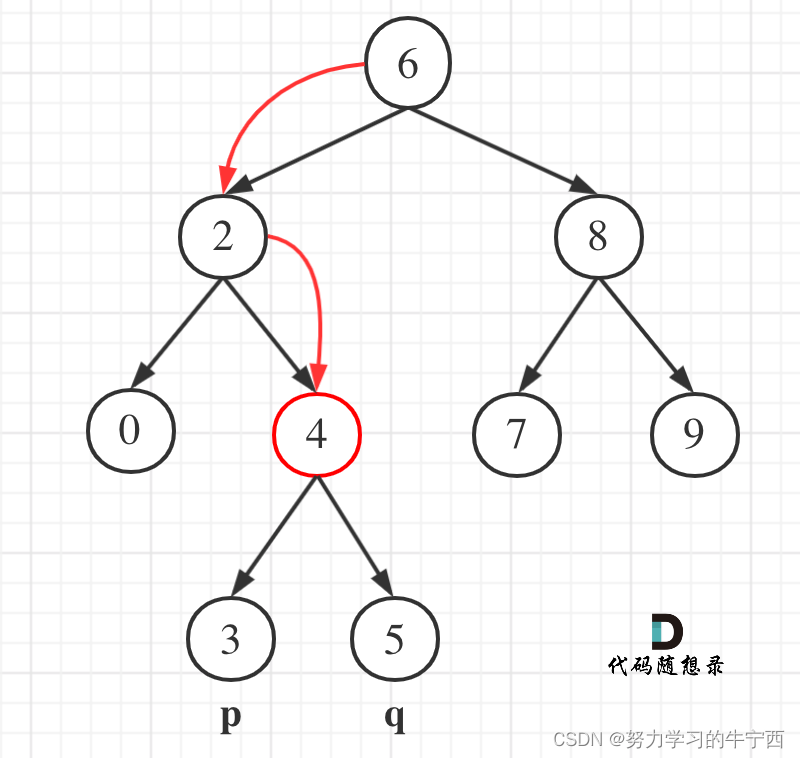
举个例子,上图中比如,p为3, q为7,遍历到root=6的时候,就在 [3,7]之间,说明p在root=6的左子树,q在root=6的右子树,不管是再向左或者向右遍历,都会错过p/q 所以root=6就是他们的最近公共祖先。
遍历顺序怎么样?
和二叉树的最近公共祖先不同,普通二叉树求最近公共祖先需要使用回溯,从底向上来查找,二叉搜索树就不用了,因为搜索树有序(相当于自带方向),那么只要从上向下遍历就可以了。那么我们可以采用前序遍历(其实这里没有中节点的处理逻辑,遍历顺序无所谓了)。example如上图所示:p为节点3,q为节点5;可以看出直接按照指定的方向,就可以找到节点4,为最近公共祖先,而且不需要遍历整棵树,找到结果直接返回!
2. 代码实现
递归三部曲如下:
确定递归函数返回值以及参数
参数就是当前节点,以及两个结点 p、q;返回值是要返回最近公共祖先,所以是TreeNode ;
class Solution: def lowestCommonAncestor(self, root: 'TreeNode', p: 'TreeNode', q: 'TreeNode') -> 'TreeNode':确定终止条件
遇到空返回就可以了,代码如下:
if root == None: return None其实都不需要这个终止条件,因为题目中说了p、q 为不同节点且均存在于给定的二叉搜索树中。也就是说一定会找到公共祖先的,所以并不存在遇到空的情况;
确定单层递归的逻辑
在遍历二叉搜索树的时候就是寻找区间[p->val, q->val](注意这里是左闭又闭);那么如果 cur->val 大于 p->val,同时 cur->val 大于q->val,那么就应该向左遍历(说明目标区间在左子树上);需要注意的是此时不知道p和q谁大,所以两个都要判断
if root.val > p.val and root.val > q.val: return self.lowestCommonAncestor(root.left, p, q)讨论此时递归函数的返回值
细心的同学会发现,在这里调用递归函数的地方,把递归函数的返回值left,直接return。在**二叉树:公共祖先问题 (opens new window)**中,如果递归函数有返回值,如何区分要搜索一条边,还是搜索整个树。
搜索一条边的写法:
if (递归函数(root->left)) return ; if (递归函数(root->right)) return ;搜索整个树写法:
left = 递归函数(root->left); right = 递归函数(root->right); left与right的逻辑处理;本题就是标准的搜索一条边的写法,遇到递归函数的返回值,如果不为空,立刻返回。
如果 cur->val 小于 p->val,同时 cur->val 小于 q->val,那么就应该向右遍历(目标区间在右子树)。
if root.val < p.val and root.val < q.val: return self.lowestCommonAncestor(root.right, p, q)剩下的情况,就是cur节点在区间(p->val <= cur->val && cur->val <= q->val)或者 (q->val <= cur->val && cur->val <= p->val)中,那么cur就是最近公共祖先了,直接返回cur。
return root
那么整体递归代码如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# 递归解法
# time:O(Height)=O(N);space:O(Height)=O(N)
'''
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
"""
:type root: TreeNode
:type p: TreeNode
:type q: TreeNode
:rtype: TreeNode
"""
if root == None: return
if root.val > p.val and root.val > q.val:
left = self.lowestCommonAncestor(root.left,p,q)
if left != None: return left
elif root.val < p.val and root.val < q.val:
right = self.lowestCommonAncestor(root.right,p,q)
if right != None: return right
return root
精简后代码如下:
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, x):
# self.val = x
# self.left = None
# self.right = None
# 递归解法
# time:O(Height)=O(N);space:O(Height)=O(N)
class Solution(object):
def lowestCommonAncestor(self, root, p, q):
if root.val > p.val and root.val > q.val:
return self.lowestCommonAncestor(root.left,p,q)
elif root.val < p.val and root.val < q.val:
return self.lowestCommonAncestor(root.right,p,q)
return root
3. 复杂度分析
时间复杂度:O(height) = O(N)
height为二叉树的高度,因为是二叉搜索树,我们只需呀沿着一条特定的路径遍历下去,不需要遍历所有节点,所以时间复杂度为O(height),在最坏情况下,二叉树为链式的树,时间复杂度为O(N);
空间复杂度:O(height)=O(N)
height为二叉树的高度,空间开销为递归压栈的开销,在最坏情况下,二叉树为链式的树,空间复杂度为O(N)。
4. 思考与收获
迭代写法:二叉搜索树的迭代法甚至比递归更容易理解,也是因为其有序性(自带方向性),按照目标区间找就行了;
# 迭代法 # time:O(height)=O(N);space:O(height)=O(N) class Solution(object): def lowestCommonAncestor(self, root, p, q): if root == None: return None while root: if root.val > p.val and root.val >q.val: root = root.left elif root.val < p.val and root.val <q.val: root = root.right else: return root return None二叉搜索树的最近祖先问题其实比普通二叉树的公共祖先问题要简单的多,不用使用回溯,二叉搜索树自带方向性,可以方便的从上向下查找目标区间,遇到目标区间内的节点,直接返回;
Reference: 代码随想录 (programmercarl.com)
本题学习时间:60分钟。
LeetCode701. 二叉树中的插入操作
链接: 701. 二叉搜索树中的插入操作 - 力扣(LeetCode)
1. 思路
其实这道题目其实是一道简单题目,但是题目中的提示:有多种有效的插入方式,还可以重构二叉搜索树,一下子吓退了不少人,瞬间感觉题目复杂了很多;其实可以不考虑题目中提示所说的改变树的结构的插入方式。
很重要的一点是,在二叉搜索树中插入任何节点,都可以在叶子节点中找到对应的位置,只要遍历二叉搜索树,找到空节点 插入元素就可以了,那么这道题其实就简单了。
2. 代码实现
实现方式一:递归有返回值
递归三部曲:
确定递归函数参数以及返回值
参数就是根节点指针,以及要插入元素,这里递归函数要不要有返回值呢?可以有,也可以没有,但递归函数如果没有返回值的话,实现是比较麻烦的,下面也会给出其具体实现代码。有返回值的话,可以利用返回值完成新加入的节点与其父节点的赋值操作。(下面会进一步解释)递归函数的返回类型为节点类型TreeNode *
class Solution: def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:确定终止条件
终止条件就是找到遍历的节点为null的时候,就是要插入节点的位置了,并把插入的节点返回。代码如下:
# Base Case if not root: return TreeNode(val)这里把添加的节点返回给上一层,就完成了父子节点的赋值操作了,详细再往下看。
确定单层递归的逻辑
此时要明确,需要遍历整棵树么?别忘了这是搜索树,遍历整棵搜索树简直是对搜索树的侮辱,哈哈。搜索树是有方向了,可以根据插入元素的数值,决定递归方向。代码如下:
if val < root.val: root.left = self.insertIntoBST(root.left, val) if root.val < val: root.right = self.insertIntoBST(root.right, val) return root到这里,大家应该能感受到,如何通过递归函数返回值完成了新加入节点的父子关系赋值操作了,下一层将加入节点返回,本层用root->left或者root->right将其接住。
整体代码如下:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def insertIntoBST(self, root: TreeNode, val: int) -> TreeNode:
# 返回更新后的以当前root为根节点的新树,方便用于更新上一层的父子节点关系链
# Base Case
if not root: return TreeNode(val)
# 单层递归逻辑:
if val < root.val:
# 将val插入至当前root的左子树中合适的位置
# 并更新当前root的左子树为包含目标val的新左子树
root.left = self.insertIntoBST(root.left, val)
if root.val < val:
# 将val插入至当前root的右子树中合适的位置
# 并更新当前root的右子树为包含目标val的新右子树
root.right = self.insertIntoBST(root.right, val)
# 返回更新后的以当前root为根节点的新树
return root
实现方式二: 递归无返回值
刚刚说了递归函数不用返回值也可以,找到插入的节点位置,直接让其父节点指向插入节点,结束递归,也是可以的。
递归法 - 无返回值
那么递归函数定义如下:
TreeNode* parent; // 记录遍历节点的父节点
void traversal(TreeNode* cur, int val)
没有返回值,需要记录上一个节点(parent),遇到空节点了,就让parent左孩子或者右孩子指向新插入的节点。然后结束递归。
# 递归 无返回值
# time:O(height)= O(N);space:O(height)=O(N)
class Solution(object):
def insertIntoBST(self, root, val):
"""
:type root: TreeNode
:type val: int
:rtype: TreeNode
"""
global parent
parent = None
if root == None: return TreeNode(val)
self.traversal(root,val)
return root
def traversal(self,node,val):
global parent
# base case 如果遇到了空,说明找到了节点该插入的地方
if parent != None and node == None:
newNode = TreeNode(val)
if parent.val < val:
parent.right = newNode
elif parent.val > val:
parent.left = newNode
return
# parent的作用只有运行到node==None的时候,发挥
# parent记录当前node的前一个节点
parent = node
if node.val < val:
self.traversal(node.right,val)
elif node.val > val:
self.traversal(node.left,val)
可以看出还是麻烦一些的。我之所以举这个例子,是想说明通过递归函数的返回值完成父子节点的赋值是可以带来便利的。
网上千变一律的代码,可能会误导大家认为通过递归函数返回节点 这样的写法是天经地义,其实这里是有优化的!
实现方式三:迭代法
迭代法与无返回值的递归函数的思路大体一致;在迭代法遍历过程中,需要记录当前节点的父节点,这样才可以做插入的操作,之前有用过双指针的技巧,这里也一样。
# 迭代法
# time:O(height)= O(N);space:O(1)
class Solution(object):
def insertIntoBST(self, root, val):
"""
:type root: TreeNode
:type val: int
:rtype: TreeNode
"""
if root == None: return TreeNode(val)
parent = None
cur = root
# 用while循环不断地找新节点的parent
while cur:
if cur.val > val:
parent = cur
cur = cur.left
elif cur.val < val:
parent = cur
cur = cur.right
# 运行到这意味着已经跳出上面的while循环,
# 同时意味着新节点的parent已经被找到.
# parent已被找到, 新节点已经ready. 把两个节点黏在一起就好了.
if parent.val > val:
parent.left = TreeNode(val)
elif parent.val < val:
parent.right = TreeNode(val)
return root
3. 复杂度分析
两个递归法:
时间复杂度:O(height) = O(N)
height为二叉树的高度,因为是二叉搜索树,我们只需呀沿着一条特定的路径遍历下去,不需要遍历所有节点,所以时间复杂度为O(height),在最坏情况下,二叉树为链式的树,时间复杂度为O(N);
空间复杂度:O(height)=O(N)
height为二叉树的高度,空间开销为递归压栈的开销,在最坏情况下,二叉树为链式的树,空间复杂度为O(N)。
迭代法:
时间复杂度:O(height) = O(N)
height为二叉树的高度,因为是二叉搜索树,我们只需呀沿着一条特定的路径遍历下去,不需要遍历所有节点,所以时间复杂度为O(height),在最坏情况下,二叉树为链式的树,时间复杂度为O(N);
空间复杂度:O(1)
只用了常数个指针记录变量,因此为O(1)
4. 思考与收获
- 首先在二叉搜索树中的插入操作,大家不用恐惧其重构搜索树,其实根本不用重构;
- 然后在递归中,我们重点讲了如果通过递归函数的返回值完成新加入节点和其父节点的赋值操作,并强调了搜索树的有序性;
- 最后依然给出了迭代的方法,迭代的方法就需要记录当前遍历节点的父节点了,这个和没有返回值的递归函数实现的代码逻辑是一样的。
Reference:代码随想录 (programmercarl.com)
本题学习时间:60分钟。
LeetCode450.删除二叉搜索树的节点
链接: 450. 删除二叉搜索树中的节点 - 力扣(LeetCode)
1. 思路
搜索树的节点删除要比节点增加复杂的多,有很多情况需要考虑,这里就把二叉搜索树中删除节点遇到的情况都搞清楚。
有以下五种情况:
- 第一种情况:没找到删除的节点,遍历到空节点直接返回了
- 找到删除的节点
- 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点(删除6)
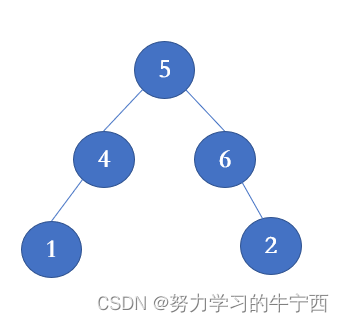
第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点(删除4)
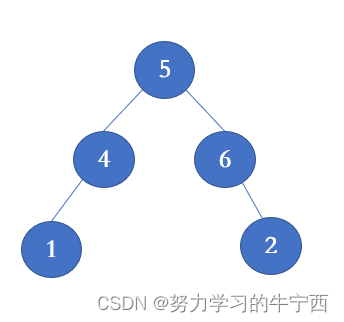
第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
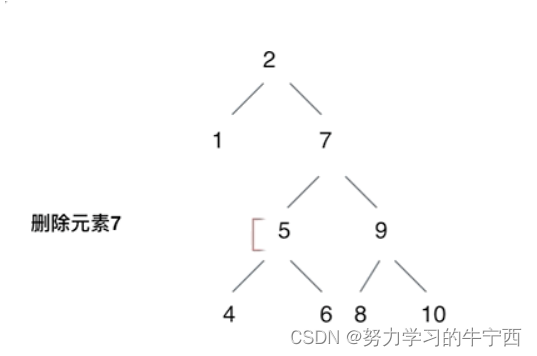
二叉搜索树中,删除元素7, 那么删除节点(元素7)的左孩子就是5,删除节点(元素7)的右子树的最左面节点是元素8。
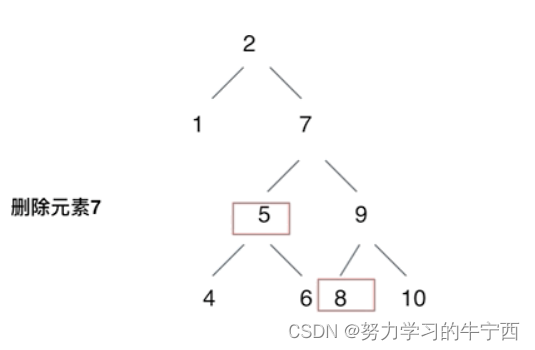
将删除节点(元素7)的左孩子放到删除节点(元素7)的右子树的最左面节点(元素8)的左孩子上,就是把5为根节点的子树移到了8的左孩子的位置。
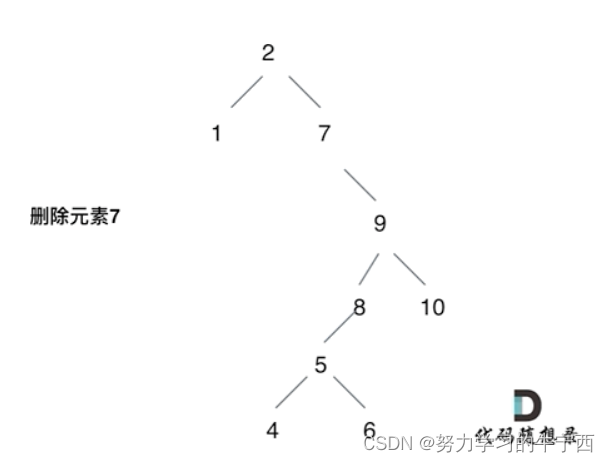
要删除的节点(元素7)的右孩子(元素9)为新的根节点。.
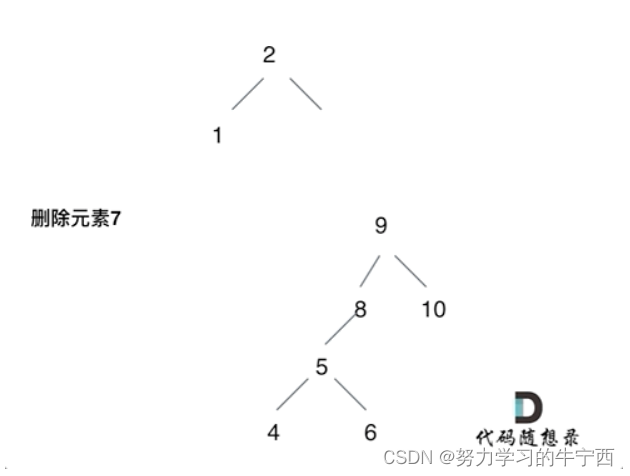
这样就完成删除元素7的逻辑,最好动手画一个图,尝试删除一个节点试试。
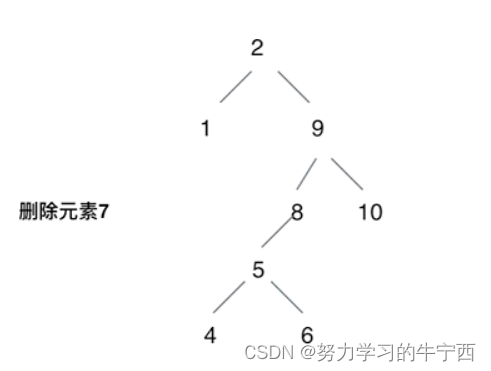
2. 代码实现
# 递归解法
# time:O(height)=O(N);space:O(Height)=O(N)
class Solution(object):
def deleteNode(self, root, key):
"""
:type root: TreeNode
:type key: int
:rtype: TreeNode
"""
# 第一种情况:没找到删除的节点,遍历到空节点直接返回了
if root == None: return None
# 找到val了
if root.val == key:
# 第二种情况:左右孩子都为空(叶子节点),
# 直接删除节点, 返回NULL为根节点
if root.left == None and root.right == None:
return None
# 第三种情况:其左孩子为空,右孩子不为空,
# 删除节点,右孩子补位 ,返回右孩子为根节点
elif root.left == None and root.right != None:
return root.right
# 第四种情况:其右孩子为空,左孩子不为空,
# 删除节点,左孩子补位,返回左孩子为根节点
elif root.left != None and root.right == None:
return root.left
# 第五种情况:左右孩子节点都不为空,
# 则将删除节点的左子树放到删除节点的
# 右子树的最左面节点的左孩子的位置
# 并返回删除节点右孩子为新的根节点。
else:
# 找右子树最左面的节点
cur = root.right
while cur.left:
cur = cur.left
# 把要删除的节点(root)左子树放在cur的左孩子的位置
cur.left = root.left
# 返回旧root的右孩子作为新root
return root.right
if root.val > key:
root.left = self.deleteNode(root.left,key)
elif root.val < key:
root.right = self.deleteNode(root.right,key)
return root
3. 复杂度分析
时间复杂度:O(n)
其中 n 为 root 的节点个数。最差情况下,需要遍历一次树。
空间复杂度:O(n)
其中 n 为 root 的节点个数。递归的深度最深为 O(n)。
4. 思考与收获
(二刷再看)二叉树的普通删除方式
这里我在介绍一种通用的删除,普通二叉树的删除方式(没有使用搜索树的特性,遍历整棵树),用交换值的操作来删除目标节点。
代码中目标节点(要删除的节点)被操作了两次:
- 第一次是和目标节点的右子树最左面节点交换。
- 第二次直接被NULL覆盖了。
思路有点绕,感兴趣的同学可以画图自己理解一下。
class Solution { public: TreeNode* deleteNode(TreeNode* root, int key) { if (root == nullptr) return root; if (root->val == key) { if (root->right == nullptr) { // 这里第二次操作目标值:最终删除的作用 return root->left; } TreeNode *cur = root->right; while (cur->left) { cur = cur->left; } swap(root->val, cur->val); // 这里第一次操作目标值:交换目标值其右子树最左面节点。 } root->left = deleteNode(root->left, key); root->right = deleteNode(root->right, key); return root; } };(二刷再看)迭代做法
删除节点的迭代法还是复杂一些的,但其本质我在递归法里都介绍了,最关键就是删除节点的操作
class Solution { private: // 将目标节点(删除节点)的左子树放到 目标节点的右子树的最左面节点的左孩子位置上 // 并返回目标节点右孩子为新的根节点 // 是动画里模拟的过程 TreeNode* deleteOneNode(TreeNode* target) { if (target == nullptr) return target; if (target->right == nullptr) return target->left; TreeNode* cur = target->right; while (cur->left) { cur = cur->left; } cur->left = target->left; return target->right; } public: TreeNode* deleteNode(TreeNode* root, int key) { if (root == nullptr) return root; TreeNode* cur = root; TreeNode* pre = nullptr; // 记录cur的父节点,用来删除cur while (cur) { if (cur->val == key) break; pre = cur; if (cur->val > key) cur = cur->left; else cur = cur->right; } if (pre == nullptr) { // 如果搜索树只有头结点 return deleteOneNode(cur); } // pre 要知道是删左孩子还是右孩子 if (pre->left && pre->left->val == key) { pre->left = deleteOneNode(cur); } if (pre->right && pre->right->val == key) { pre->right = deleteOneNode(cur); } return root; } };会发现二叉搜索树删除节点比增加节点复杂的多。因为二叉搜索树添加节点只需要在叶子上添加就可以的,不涉及到结构的调整,而删除节点操作涉及到结构的调整。这里我们依然使用递归函数的返回值来完成把节点从二叉树中移除的操作。这里最关键的逻辑就是第五种情况(删除一个左右孩子都不为空的节点),这种情况一定要想清楚。而且就算想清楚了,对应的代码也未必可以写出来,所以这道题目即考察思维逻辑,也考察代码能力。
递归中我给出了两种写法,推荐大家学会第一种(利用搜索树的特性)就可以了,第二种递归写法其实是比较绕的。
最后我也给出了相应的迭代法,就是模拟递归法中的逻辑来删除节点,但需要一个pre记录cur的父节点,方便做删除操作。迭代法其实不太容易写出来,所以如果是初学者的话,彻底掌握第一种递归写法就够了。
Reference:代码随想录 (programmercarl.com)
本题学习时间:60分钟。
本篇学习时间约为3个多小时,总结近10000字;二叉搜索树的最大公共祖先比普通的二叉搜索树简单很多;在BST上插入节点不涉及到结构的调整比较简单,但是删除二叉搜索树上的节点就涉及到结构的调整了,比较复杂。(求推荐!)