HBU-NNDL 作业5：卷积

发布于：2022-10-15 ⋅ 阅读:(609) ⋅ 点赞:(0)

目录

作业1

编程实现

1 . 图1使用卷积核​编辑，输出特征图

2. 图1使用卷积核​编辑，输出特征图

3. 图2使用卷积核​编辑，输出特征图

4. 图2使用卷积核​编辑，输出特征图 

5. 图3使用卷积核​编辑，​编辑，​编辑 ，输出特征图 

作业2

一、概念

二、探究不同卷积核的作用

三、编程实现

总结

参考

作业1

编程实现

import torch.nn as nn
import torch
import matplotlib.pyplot as plt
import numpy as np
from torch.autograd import Variable



plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号 #有中文出现的情况，需要u'内容
im=np.zeros((7,6),dtype='float32')
im[:,3:]=im[:,3:]+255
print(im.shape[0], im.shape[1])
plt.imshow(im,cmap='gray')
plt.title('原图')
plt.show()
im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
k1=np.array([-1,1],dtype='float32')
k1=k1.reshape((1,1,1,2))
conv1=nn.Conv2d(1,1,(1,2),bias=False)
conv1.weight.data = torch.from_numpy(k1)  # 给卷积的 kernel 赋值
edge1 = conv1(Variable(im))  # 作用在图片上
print(edge1)
x = edge1.data.squeeze().numpy()
print(x.shape)  # 输出大小
plt.imshow(x, cmap='gray')
plt.title('卷积后的图')
plt.show()

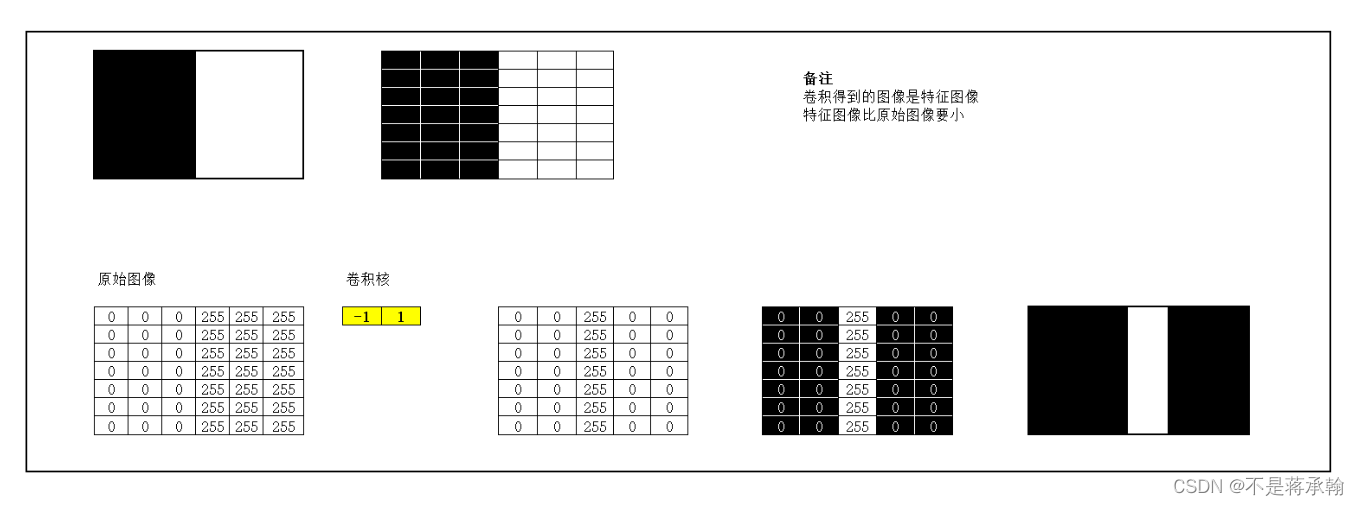
1 . 图1使用卷积核\begin{pmatrix} 1 & -1 \end{pmatrix}，输出特征图

import torch.nn as nn
import torch
import matplotlib.pyplot as plt
import numpy as np
from torch.autograd import Variable



plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号 #有中文出现的情况，需要u'内容
im=np.zeros((7,6),dtype='float32')
im[:,3:]=im[:,3:]+255
print(im.shape[0], im.shape[1])
plt.imshow(im,cmap='gray')
plt.title('原图')
plt.show()
im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
k1=np.array([1,-1],dtype='float32')
k1=k1.reshape((1,1,1,2))
conv1=nn.Conv2d(1,1,(1,2),bias=False)
conv1.weight.data = torch.from_numpy(k1)  # 给卷积的 kernel 赋值
edge1 = conv1(Variable(im))  # 作用在图片上
print(edge1)
x = edge1.data.squeeze().numpy()
print(x.shape)  # 输出大小
plt.imshow(x, cmap='gray')
plt.title('卷积后的图')
plt.show()

7 6
tensor([[[[   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.]]]], grad_fn=<ThnnConv2DBackward>)
(7, 5)

 

 

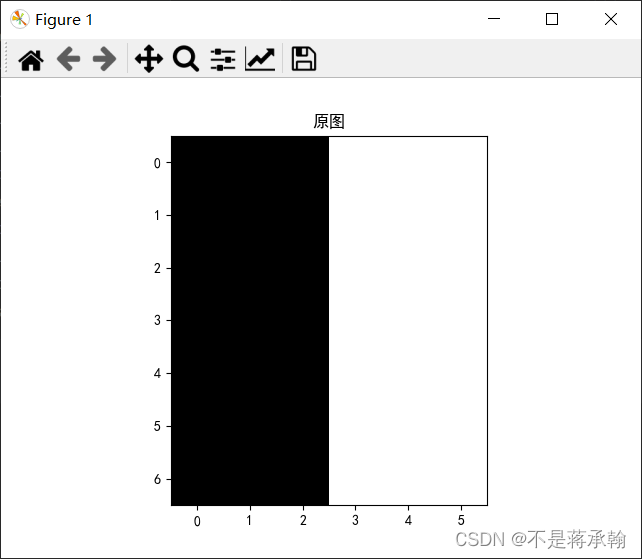
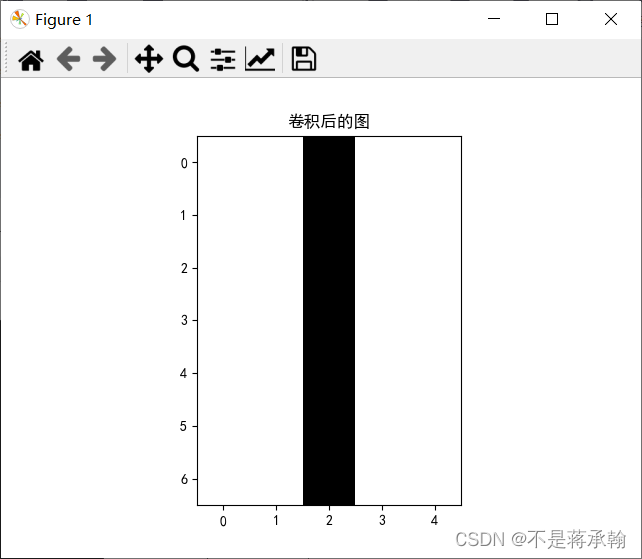
 可以看出(1,-1)卷积核的作用是左右的分界线。

2. 图1使用卷积核\begin{pmatrix} 1\\ -1\\ \end{pmatrix}，输出特征图

改变卷积核形状即可：

k1=k1.reshape((1,1,2,1))
conv1=nn.Conv2d(1,1,(2,1),bias=False)

 7 6
tensor([[[[0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0.],
          [0., 0., 0., 0., 0., 0.]]]], grad_fn=<ThnnConv2DBackward>)
(6, 6)

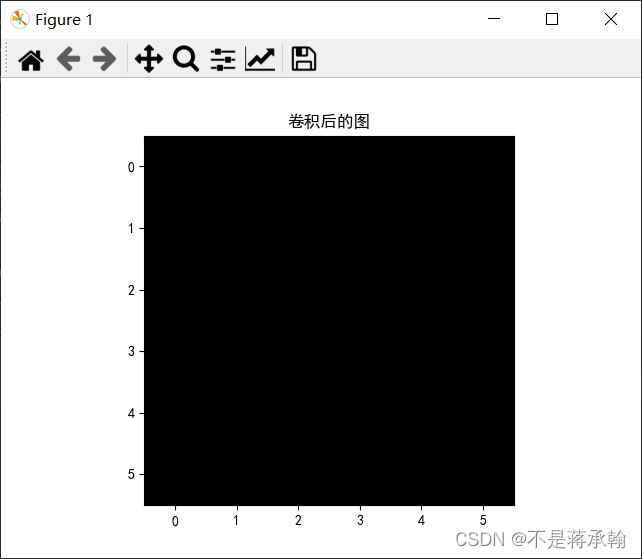
卷积核\begin{pmatrix} 1\\ -1\\ \end{pmatrix}应该是图像上下的分界线，但是图一上下无颜色差异，所以卷积后的图像全是黑色。

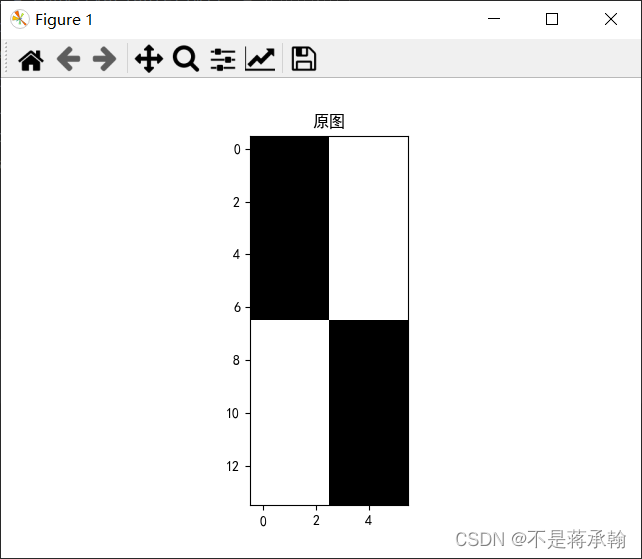
3. 图2使用卷积核\begin{pmatrix} 1 & -1 \end{pmatrix}，输出特征图

import torch.nn as nn
import torch
import matplotlib.pyplot as plt
import numpy as np
from torch.autograd import Variable



plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号 #有中文出现的情况，需要u'内容
im=np.zeros((14,6),dtype='float32')
im[:7,3:]=im[:7,3:]+255
im[7:,:3]=im[7:,:3]+255
print(im.shape[0], im.shape[1])
plt.imshow(im,cmap='gray')
plt.title('原图')
plt.show()
im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
k1=np.array([1,-1],dtype='float32')
k1=k1.reshape((1,1,1,2))
conv1=nn.Conv2d(1,1,(1,2),bias=False)
conv1.weight.data = torch.from_numpy(k1)  # 给卷积的 kernel 赋值
edge1 = conv1(Variable(im))  # 作用在图片上
print(edge1)
x = edge1.data.squeeze().numpy()
print(x.shape)  # 输出大小
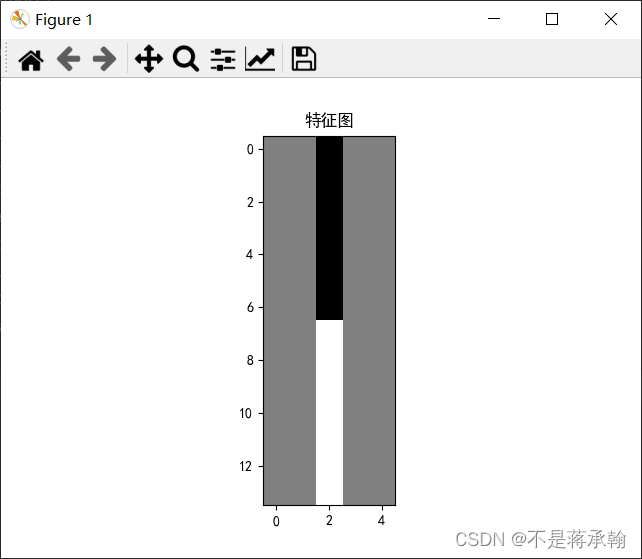
plt.imshow(x, cmap='gray')
plt.title('特征图')
plt.show()

14 6
tensor([[[[   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0., -255.,    0.,    0.],
          [   0.,    0.,  255.,    0.,    0.],
          [   0.,    0.,  255.,    0.,    0.],
          [   0.,    0.,  255.,    0.,    0.],
          [   0.,    0.,  255.,    0.,    0.],
          [   0.,    0.,  255.,    0.,    0.],
          [   0.,    0.,  255.,    0.,    0.],
          [   0.,    0.,  255.,    0.,    0.]]]], grad_fn=<ThnnConv2DBackward>)
(14, 5)

 

4. 图2使用卷积核\begin{pmatrix} 1\\ -1\\ \end{pmatrix}，输出特征图 

k1=k1.reshape((1,1,2,1))
conv1=nn.Conv2d(1,1,(2,1),bias=False)

14 6
tensor([[[[   0.,    0.,    0.,    0.,    0.,    0.],
          [   0.,    0.,    0.,    0.,    0.,    0.],
          [   0.,    0.,    0.,    0.,    0.,    0.],
          [   0.,    0.,    0.,    0.,    0.,    0.],
          [   0.,    0.,    0.,    0.,    0.,    0.],
          [   0.,    0.,    0.,    0.,    0.,    0.],
          [-255., -255., -255.,  255.,  255.,  255.],
          [   0.,    0.,    0.,    0.,    0.,    0.],
          [   0.,    0.,    0.,    0.,    0.,    0.],
          [   0.,    0.,    0.,    0.,    0.,    0.],
          [   0.,    0.,    0.,    0.,    0.,    0.],
          [   0.,    0.,    0.,    0.,    0.,    0.],
          [   0.,    0.,    0.,    0.,    0.,    0.]]]],
       grad_fn=<ThnnConv2DBackward>)
(13, 6) 

 

 

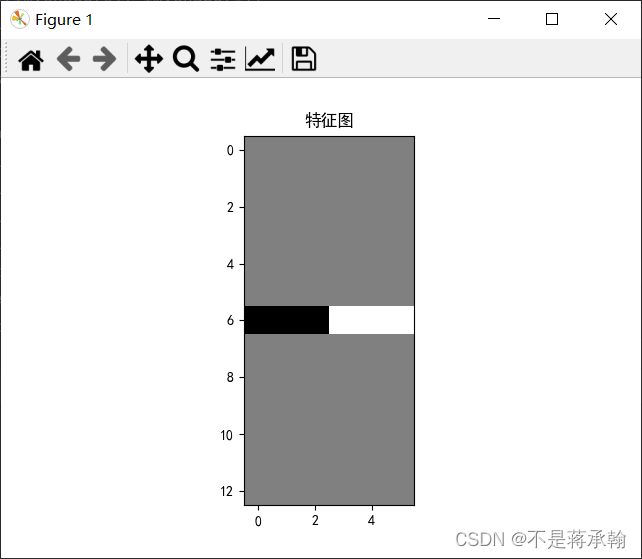
5. 图3使用卷积核\begin{pmatrix} 1 & -1 \end{pmatrix}，\begin{pmatrix} 1\\ -1\\ \end{pmatrix}，\begin{pmatrix} 1 &-1 \\ -1&1 \end{pmatrix} ，输出特征图 

import torch.nn as nn
import torch
import matplotlib.pyplot as plt
import numpy as np
from torch.autograd import Variable



plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号 #有中文出现的情况，需要u'内容
im=np.zeros((9,9),dtype='float32')
for i in range(1,8):
    im[i][i]=im[i][i]+255
    im[i][8-i]=im[i][8-i]+255
im[4][4]-=255
print(im.shape[0], im.shape[1])
plt.imshow(im,cmap='gray')
plt.title('原图')
plt.show()
im = torch.from_numpy(im.reshape((1, 1, im.shape[0], im.shape[1])))
k1=np.array([1,-1],dtype='float32')
k1=k1.reshape((1,1,1,2))
conv1=nn.Conv2d(1,1,(1,2),bias=False)
conv1.weight.data = torch.from_numpy(k1)  # 给卷积的 kernel 赋值
edge1 = conv1(Variable(im))  # 作用在图片上
print(edge1)
x = edge1.data.squeeze().numpy()
print(x.shape)  # 输出大小
plt.imshow(x, cmap='gray')
plt.title('特征图')
plt.show()

9 9
tensor([[[[   0.,    0.,    0.,    0.,    0.,    0.,    0.,    0.],
          [-255.,  255.,    0.,    0.,    0.,    0., -255.,  255.],
          [   0., -255.,  255.,    0.,    0., -255.,  255.,    0.],
          [   0.,    0., -255.,  255., -255.,  255.,    0.,    0.],
          [   0.,    0.,    0., -255.,  255.,    0.,    0.,    0.],
          [   0.,    0., -255.,  255., -255.,  255.,    0.,    0.],
          [   0., -255.,  255.,    0.,    0., -255.,  255.,    0.],
          [-255.,  255.,    0.,    0.,    0.,    0., -255.,  255.],
          [   0.,    0.,    0.,    0.,    0.,    0.,    0.,    0.]]]],
       grad_fn=<ThnnConv2DBackward>)
(9, 8) 

 

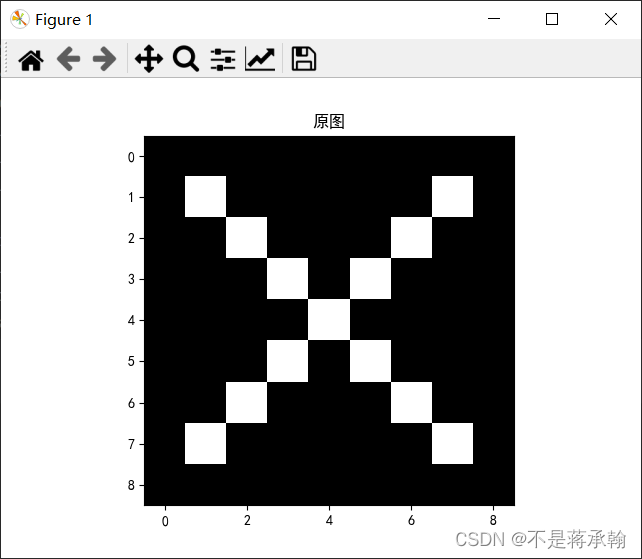
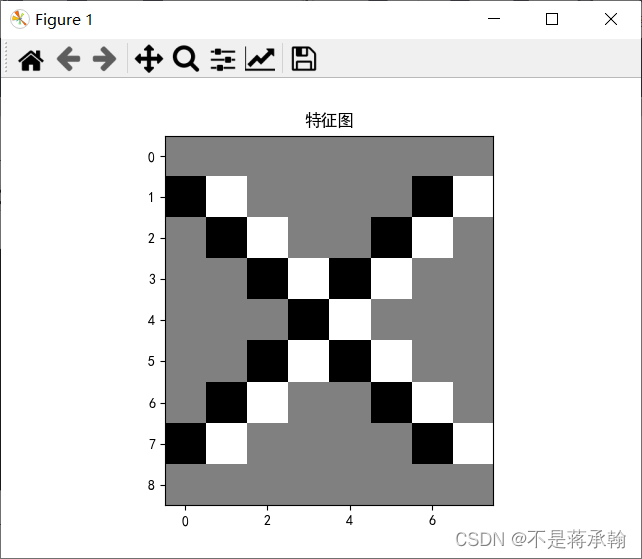
\begin{pmatrix} 1\\ -1\\ \end{pmatrix}卷积核：

k1=k1.reshape((1,1,2,1))
conv1=nn.Conv2d(1,1,(2,1),bias=False)

9 9
tensor([[[[   0., -255.,    0.,    0.,    0.,    0.,    0., -255.,    0.],
          [   0.,  255., -255.,    0.,    0.,    0., -255.,  255.,    0.],
          [   0.,    0.,  255., -255.,    0., -255.,  255.,    0.,    0.],
          [   0.,    0.,    0.,  255., -255.,  255.,    0.,    0.,    0.],
          [   0.,    0.,    0., -255.,  255., -255.,    0.,    0.,    0.],
          [   0.,    0., -255.,  255.,    0.,  255., -255.,    0.,    0.],
          [   0., -255.,  255.,    0.,    0.,    0.,  255., -255.,    0.],
          [   0.,  255.,    0.,    0.,    0.,    0.,    0.,  255.,    0.]]]],
       grad_fn=<ThnnConv2DBackward>)
(8, 9) 

 

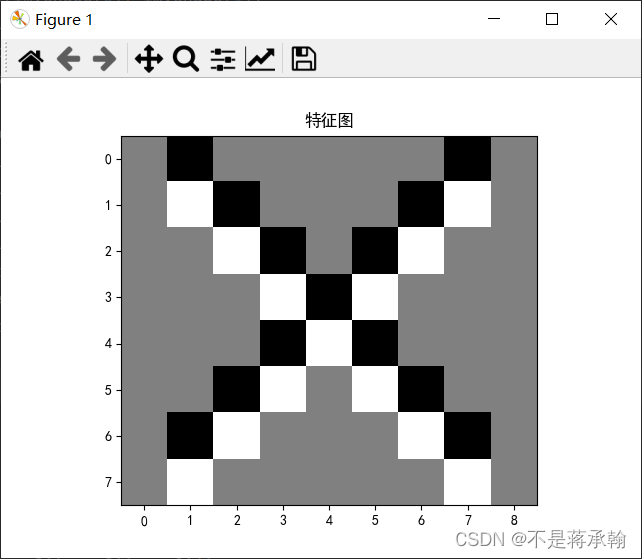
\begin{pmatrix} 1 &-1 \\ -1&1 \end{pmatrix}卷积核

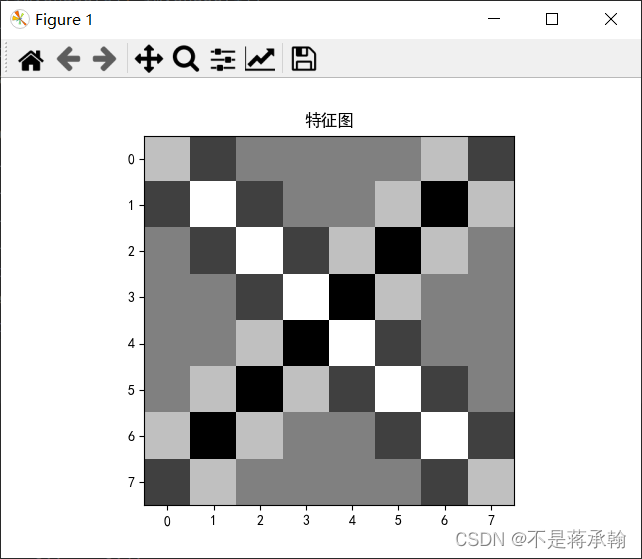
k1=np.array([[1,-1],[-1,1]],dtype='float32')
k1=k1.reshape((1,1,2,2))
conv1=nn.Conv2d(1,1,(2,2),bias=False)

9 9
tensor([[[[ 255., -255.,    0.,    0.,    0.,    0.,  255., -255.],
          [-255.,  510., -255.,    0.,    0.,  255., -510.,  255.],
          [   0., -255.,  510., -255.,  255., -510.,  255.,    0.],
          [   0.,    0., -255.,  510., -510.,  255.,    0.,    0.],
          [   0.,    0.,  255., -510.,  510., -255.,    0.,    0.],
          [   0.,  255., -510.,  255., -255.,  510., -255.,    0.],
          [ 255., -510.,  255.,    0.,    0., -255.,  510., -255.],
          [-255.,  255.,    0.,    0.,    0.,    0., -255.,  255.]]]],
       grad_fn=<ThnnConv2DBackward>)
(8, 8)

 

 

作业2

一、概念

用自己的语言描述“卷积、卷积核、特征图、特征选择、步长、填充、感受野”。

1、卷积

对卷积这个名词的理解：所谓两个函数的卷积，本质上就是先将一个函数翻转，然后进行滑动叠加。

在连续情况下，叠加指的是对两个函数的乘积求积分，在离散情况下就是加权求和，为简单起见就统一称为叠加。

整体看来是这么个过程：

翻转——>滑动——>叠加——>滑动——>叠加——>滑动——>叠加.....

多次滑动得到的一系列叠加值，构成了卷积函数。

卷积的“卷”，指的的函数的翻转，从 g(t) 变成 g(-t) 的这个过程；同时，“卷”还有滑动的意味在里面。

卷积的“积”，指的是积分/加权求和。

2、卷积核

卷积核（kernel），也叫卷积矩阵（convolution matrix），本质上是一个非常小的矩阵，最常用的是 3×3 矩阵。主要是利用核与图像之间进行卷积运算来实现图像处理，能做出模糊、锐化、凹凸、边缘检测等效果。

3、特征图

特征图（feature map）：即数据的存储图，每个卷积层都包含输入特征图（Input）和输出特征图（Output）。其包含高度、宽度、深度三个维度和通道数（channels）、批量尺寸（batch）两个参数（维度）。其shape为[f_batch, f_height, f_width,f_depth, f_channels]。需要注意最开始的输入特征图的通道数取决于图片类型，如RGB是3通道。

4、特征选择

        从N个特征中选择其中M（M<=N）个子特征，并且在M个子特征中，准则函数可以达到最优解。用具体函数评价系统所采取策略优劣的准则时,称为准则函数。
  特征选择想要做的是：选择尽可能少的子特征，模型的效果不会显著下降，并且结果的类别分布尽可能的接近真实的类别分布。

5、步长

        卷积过程中，有时需要通过填充来避免信息损失，有时也要在卷积时通过设置的步长(Stride)来压缩一部分信息。因此卷积中的步幅是另一个构建卷积神经网络的基本操作。

        Stride表示filter在原图片中水平方向和垂直方向每次的步进长度。之前我们默认stride=1。若stride=2，则表示filter每次步进长度为2，即隔一点移动一次。

6、填充

                输入图像与卷积核进行卷积后的结果中损失了部分值，输入图像的边缘被“修剪”掉了（边缘处只检测了部分像素点，丢失了图片边界处的众多信息）。这是因为边缘上的像素永远不会位于卷积核中心，而卷积核也没法扩展到边缘区域以外。

这个结果我们是不能接受的，有时我们还希望输入和输出的大小应该保持一致。为解决这个问题，可以在进行卷积操作前，对原矩阵进行边界填充（Padding），也就是在矩阵的边界上填充一些值，以增加矩阵的大小，通常都用“0”来进行填充的。

        通过填充的方法，当卷积核扫描输入数据时，它能延伸到边缘以外的伪像素，从而使输出和输入size相同。

常用的两种padding：

（1）valid padding：不进行任何处理，只使用原始图像，不允许卷积核超出原始图像边界

（2）same padding：进行填充，允许卷积核超出原始图像边界，并使得卷积后结果的大小与原来的一致

7、感受野

        感受野(receptive field)这一概念来自于生物神经科学，是指感觉系统中的任一神经元，其所受到的感受器神经元的支配范围。感受器神经元就是指接收感觉信号的最初级神经元

        在卷积神经网络中，感受野(receptive field)不像输出由整个网络输入所决定的全连接网络那样，它是可以存在于网络中任意某层，输出仅由输入部分决定

        就是指输出feature map上某个元素受输入图像上影响的区域

二、探究不同卷积核的作用

1、模糊滤波核

消除了相邻像素之间的差异

2、bottom sobel

仅用于显示特定方向上相邻像素值的差异：left sobel，right sobel，top sobel，bottom sobel。

3、浮雕效果

通过强调像素的差在给定方向的Givens深度错觉。

4、原图

5、大纲（outline）

一个轮廓内核（也称为“边缘”的内核）用于突出显示的像素值大的差异。具有接近相同强度的相邻像素旁边的像素在新图像中将显示为黑色，而强烈不同的相邻像素相邻的像素将显示为白色。

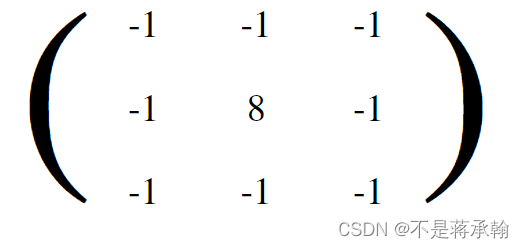
6、锐化

强调在相邻的像素值的差异，使图片看起来更加的生动

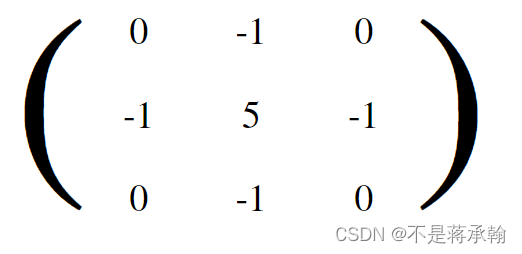
三、编程实现

1、实现灰度图的边缘检测、锐化、模糊。

import torch
import numpy as np
from PIL import Image
import matplotlib.pyplot as plt


plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号 #有中文出现的情况，需要u'内容
# 读取灰度图
img = Image.open("bombshit.png").convert('L')
plt.imshow(img, cmap='gray')
plt.title('原图')
plt.show()
img = np.array(img, dtype='float32').reshape(1, 1, img.size[1], img.size[0])
img = torch.from_numpy(img)

# 定义卷积层，单通道输入，单通道输出，因此需要1个3*3的卷积核
conv_layer = torch.nn.Conv2d(
    in_channels=1,
    out_channels=1,
    kernel_size=3,
    stride=1,
    padding=1
)

# 边缘检测卷积核
outline_kernel = [[-1, -1, -1],
                  [-1, 8, -1],
                  [-1, -1, -1]]
# 锐化卷积核
# sharpen_kernel = [[0, -1, 0],
#                   [-1, 5, -1],
#                   [0, -1, 0]]
# 模糊卷积核
# blur_kernel =    [[0.0625, 0.125, 0.0625],
#                   [0.125, 0.25, 0.125],
#                   [0.0625, 0.125, 0.0625]]
kernel = torch.from_numpy(np.array(outline_kernel, dtype='float32').reshape(1, 1, 3, 3))
conv_layer.weight.data = kernel

# 推理
img_output = conv_layer(img)

# 展示
plt.imshow(img_output.data.squeeze().numpy(), cmap='gray')
plt.title('特征图')
plt.show()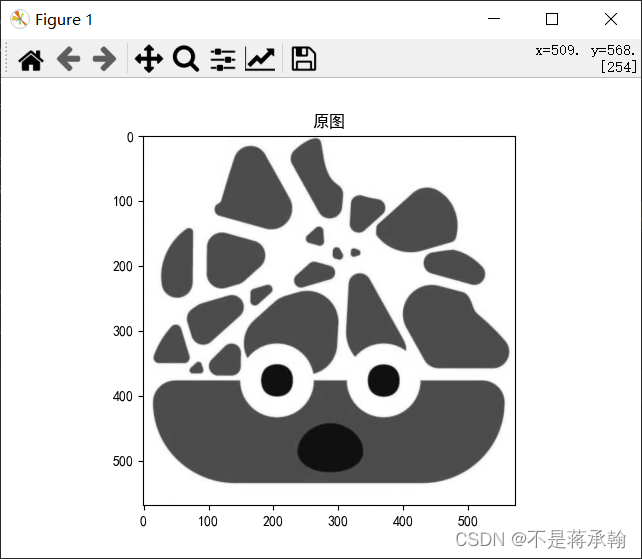

 

 边缘检测：

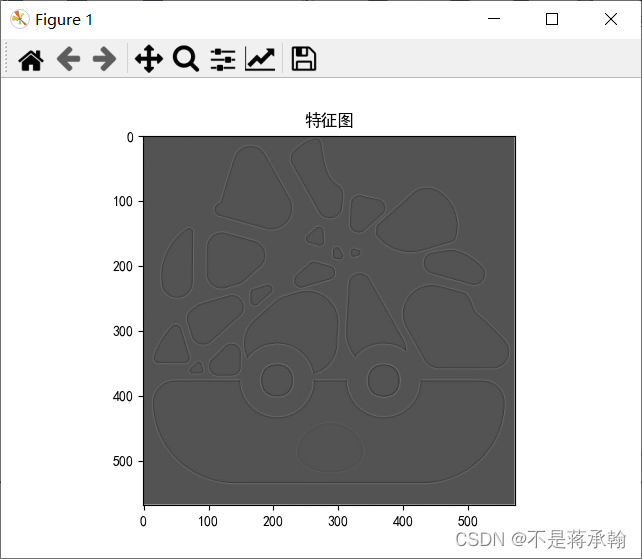
 但是这个实现的效果和网站上实现的效果不太一样：

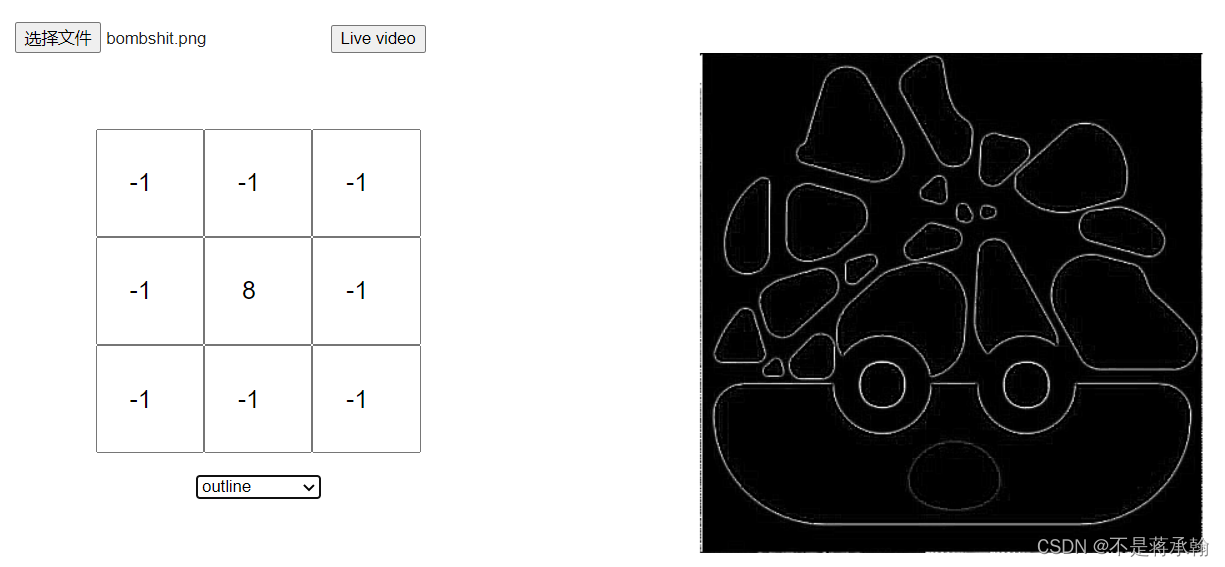
 这个问题我和室友真不想再学了的博客_CSDN博客-领域博主研究了一下，应该是数据溢出0-255范围内了，所以加了一段代码，将小于0的变成0，将大于255的变成255

for i in range(img_output.shape[2]):
    for j in range(img_output.shape[3]):
        if img_output[0][0][i][j]>255:
            img_output[0][0][i][j]=255
        if img_output[0][0][i][j]<0:
            img_output[0][0][i][j]=0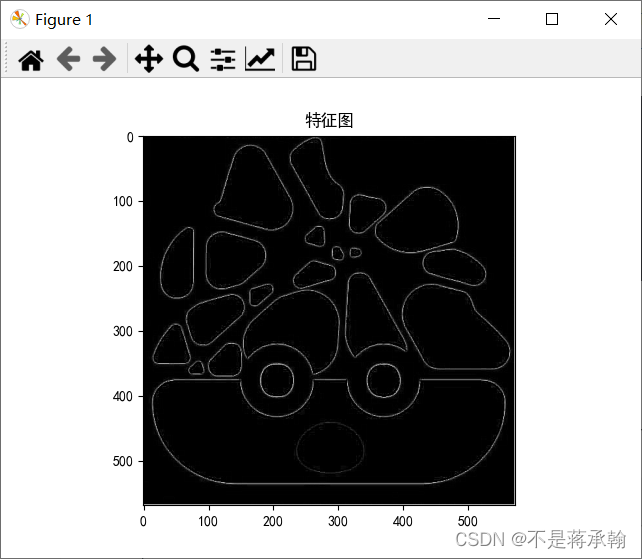

 

 这下就一样了。

锐化：

 

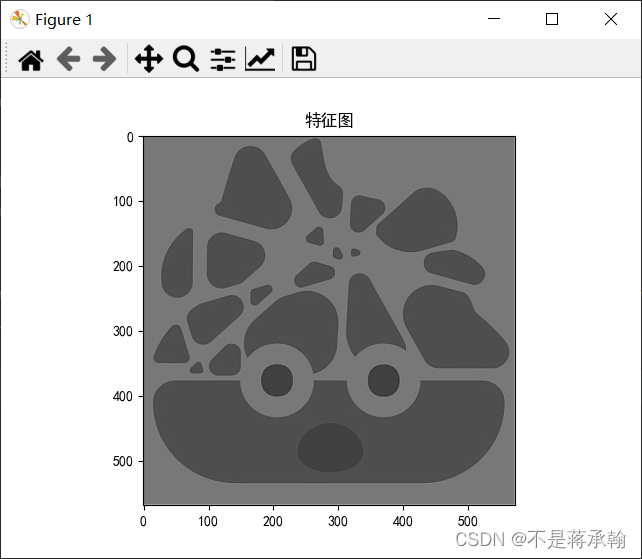
这个效果也不一样

 

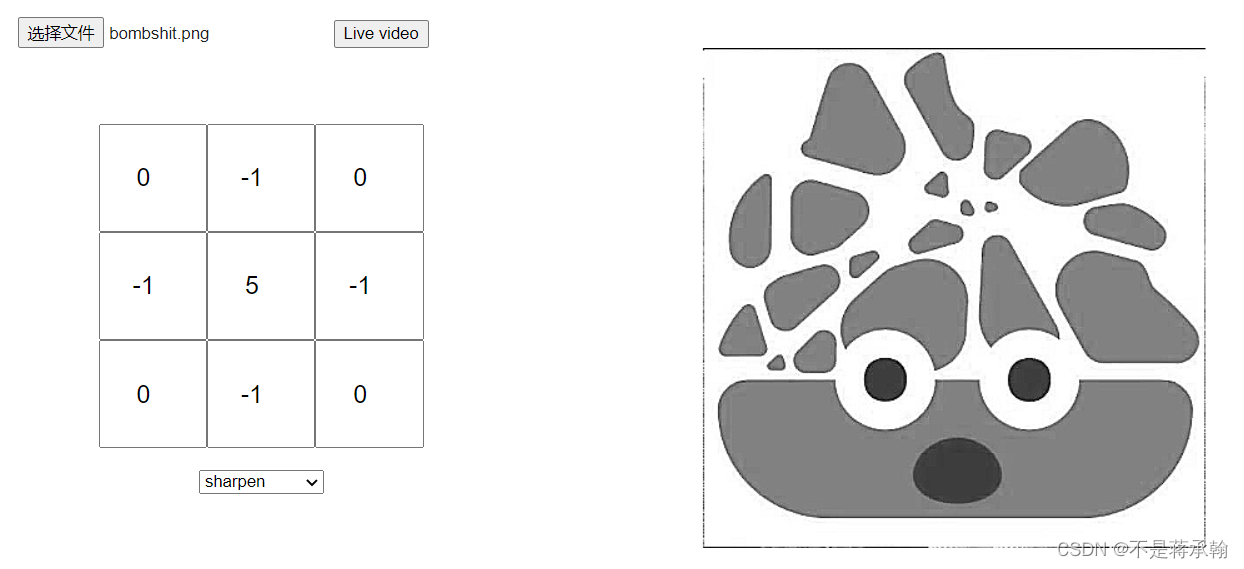
 同理改一下

 

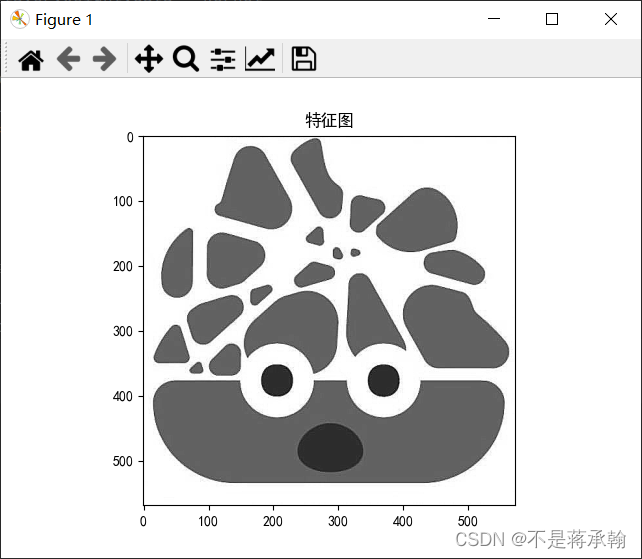
 模糊：

 

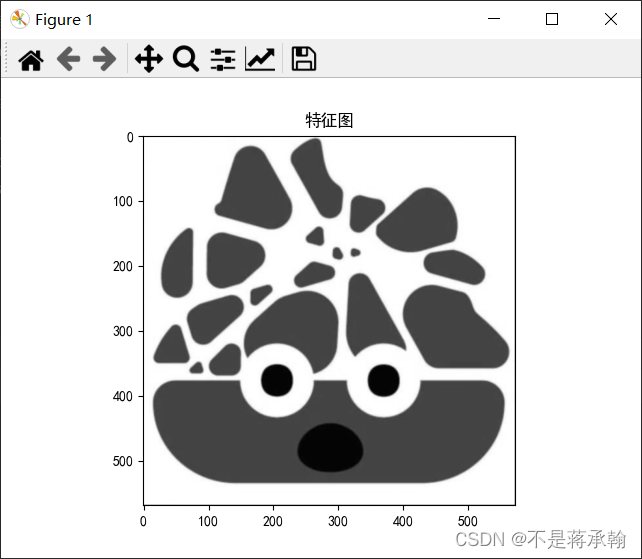
这个看不出太大的区别，但是也改一下

 

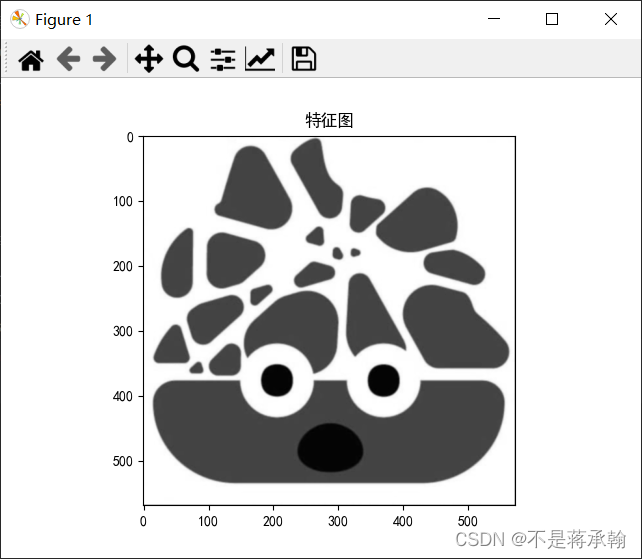
看了模糊化数据没有怎么溢出。

 

2、调整卷积核参数，测试并总结。

调整步长为2：

边缘检测：

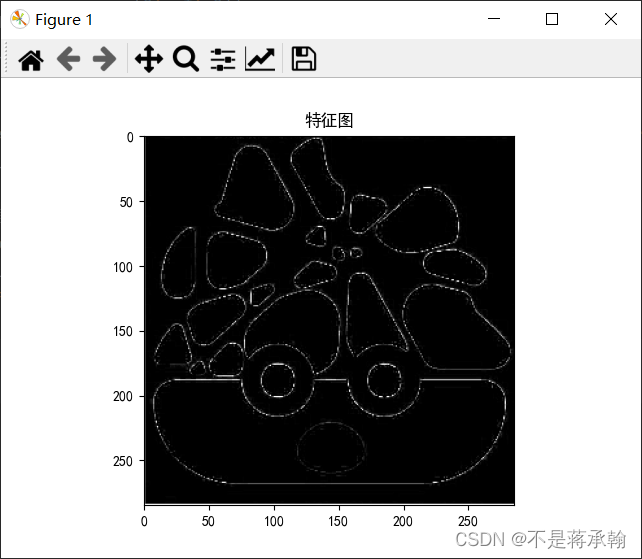
锐化：

 

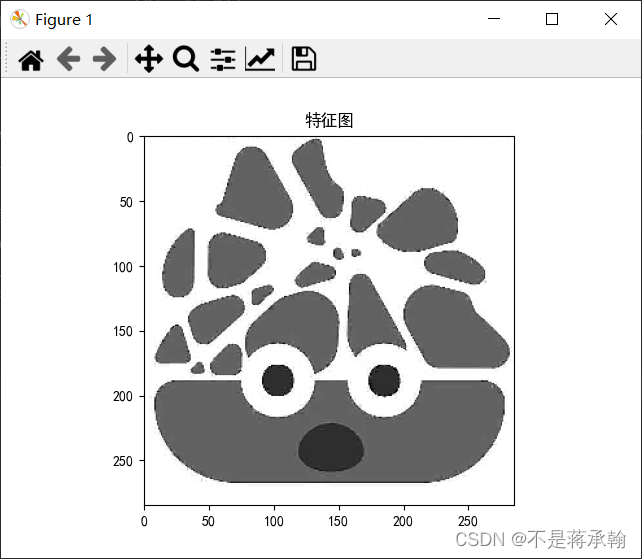
 模糊：

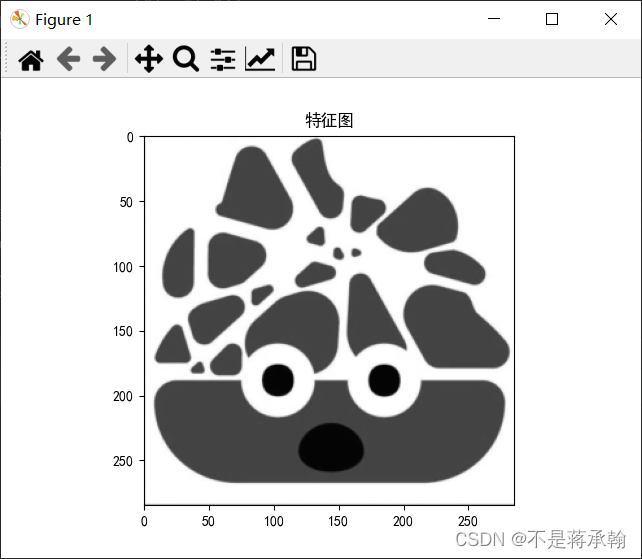
可以看出，步长变大后，图片锯齿变明显了，不是很清晰。

将填充从1变为0：

边缘检测：

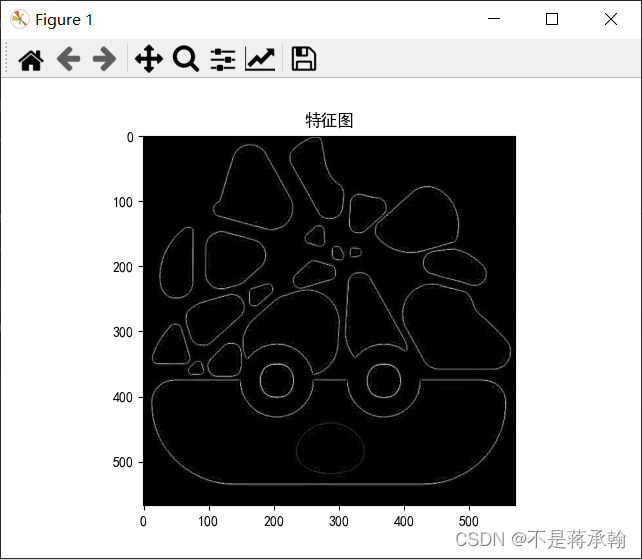
锐化：

 

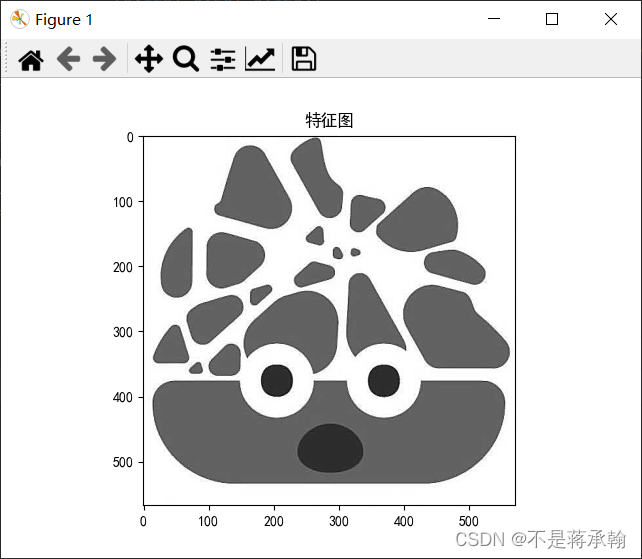
 模糊：

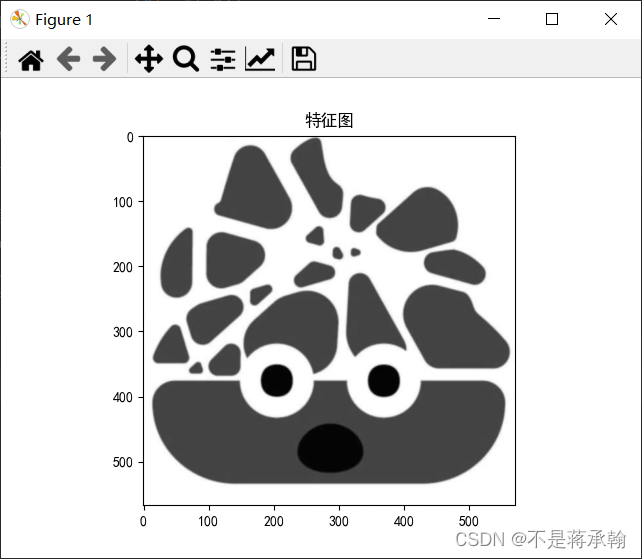
可以看出改变padding差别不是很大 

3、使用不同尺寸图片，测试并总结。

        经测试，由于卷积核本身较小，因此只能作用于较小尺度，所以小尺寸图片看起来效果会好些。但是图片尺寸对于卷积实际上是无影响。

4、探索更多类型卷积核。

浮雕：

# 浮雕卷积核
emboss_kernel = [[-2, -1, 0],
                  [-1, 1, -1],
                  [0, 1, 2]]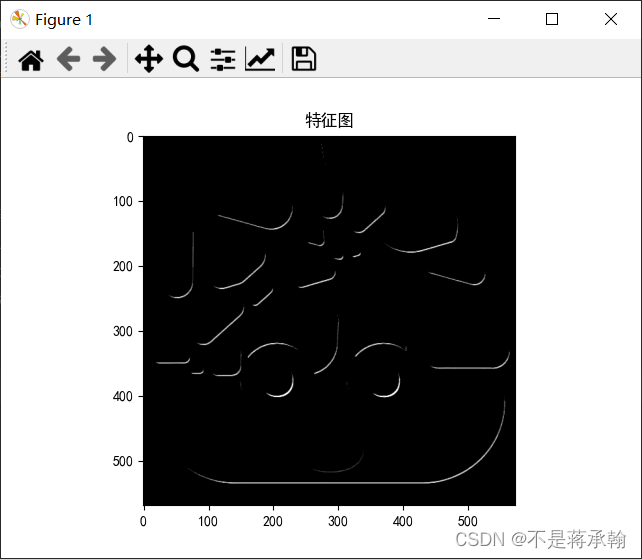

 

emboss通过强调像素的差在给定方向的Givens深度错觉，这个出来的效果挺恐怖的，把可爱屎炸变得阴森。

bottom sobel：

# bottom sobel卷积核
bsobel_kernel = [[-1, -2, -1],
                  [0, 0, 0],
                  [1, 2, 1]]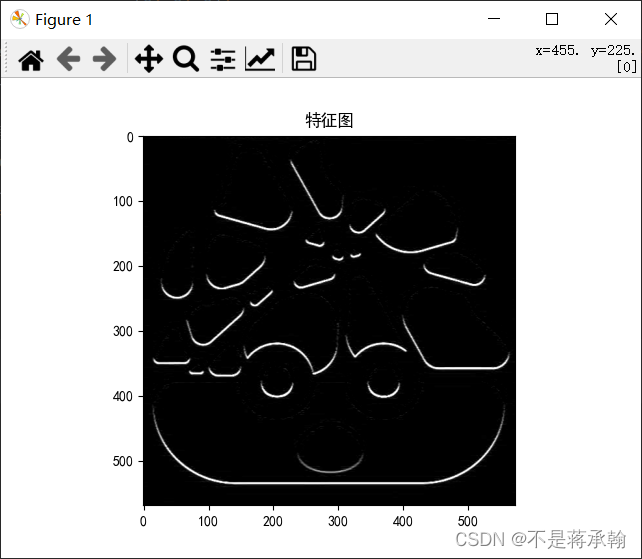

 

 用于显示特定方向上相邻像素值的差异，看起来和浮雕差不多。

放一张图像各类滤波的关系图

 

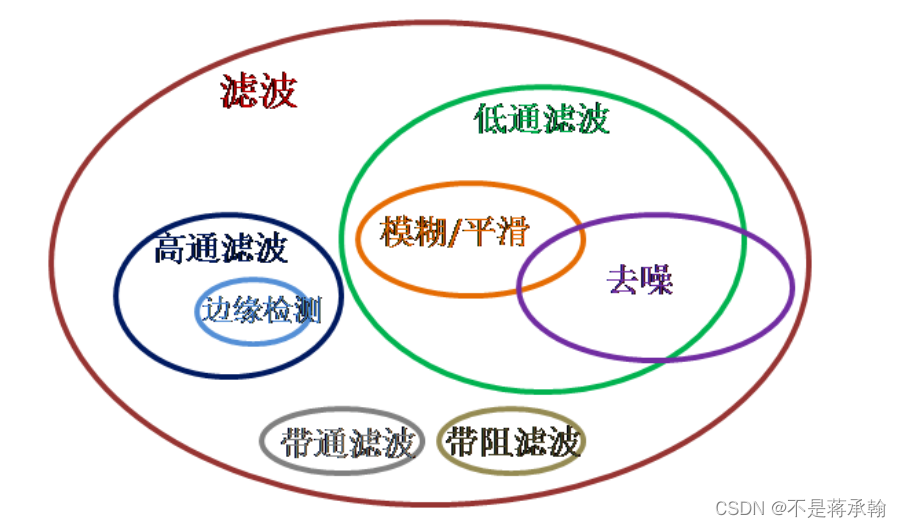
5、尝试彩色图片边缘检测。

        一般对彩色图片边缘检测会先把彩色图片转换成灰度图或者二值图像。当使用CNN进行边缘检测时优先考虑将其转成灰度图然后进行边缘检测。

import torch
import numpy as np
from torch import nn
from PIL import Image
from torch.autograd import Variable
import torch.nn.functional as F
import cv2

def edge_conv2d(im):
    # 用nn.Conv2d定义卷积操作
    conv_op = nn.Conv2d(3, 3, kernel_size=3, padding=1, bias=False)
    # 定义sobel算子参数，所有值除以3个人觉得出来的图更好些
    sobel_kernel = np.array([[-1, -1, -1], [-1, 8, -1], [-1, -1, -1]], dtype='float32') / 3
    # 将sobel算子转换为适配卷积操作的卷积核
    sobel_kernel = sobel_kernel.reshape((1, 1, 3, 3))
    # 卷积输出通道，这里我设置为3
    sobel_kernel = np.repeat(sobel_kernel, 3, axis=1)
    # 输入图的通道，这里我设置为3
    sobel_kernel = np.repeat(sobel_kernel, 3, axis=0)

    conv_op.weight.data = torch.from_numpy(sobel_kernel)


    edge_detect = conv_op(im)

    # 将输出转换为图片格式
    edge_detect = edge_detect.squeeze().detach().numpy()
    return edge_detect

def edge_extraction():
    im = cv2.imread('bombshit.png', flags=1)
    im = np.transpose(im, (2, 0, 1))
    # 添加一个维度，对应于pytorch模型张量(B, N, H, W)中的batch_size
    im = im[np.newaxis, :]
    im = torch.Tensor(im)
    edge_detect = edge_conv2d(im)
    edge_detect = np.transpose(edge_detect, (1, 2, 0))
    # cv2.imshow('edge.jpg', edge_detect)
    cv2.imwrite('edge-2.jpg', edge_detect)

if __name__ == "__main__":
    edge_extraction()

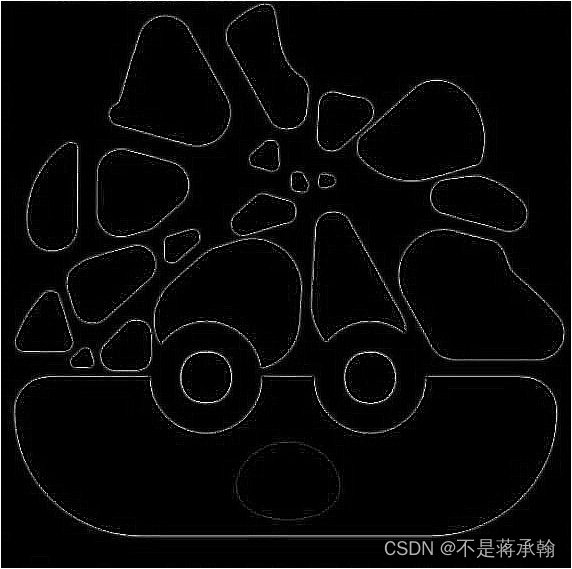
总结

        这次作业深入了解了卷积原理，明白了不同卷积核的作用。

        但是，使用pytorch实现的图像边缘检测和Image Kernels explained visually上的边缘检测有所差异，感觉直接将溢出的数变为0和255还是有不妥，在接下来的学习中希望可以把这个问题研究明白。

参考

【图像处理】彩色图像边缘检测_artzers的博客-CSDN博客_彩色边缘检测

本文含有隐藏内容，请 开通VIP 后查看

网站公告

：

今日签到

点亮在社区的每一天
去签到

热门文章

最新发布