目录
一、平衡二叉树
1)概述
二叉排序树的查找效率与二叉树的形状有关
1. 对于按给定序列的二叉排序树,若其
左、右子树均匀分布,则查找过程类似于有序表的二分查找,时间复杂度为O(log2n)2. 若给定序列
原来有序,则建立的二叉排序树就蜕化为单链表,其查找效率同顺序查找一样,时间复杂度为O(n)在构造二叉排序树的过程中,当出现左右子树分布不均匀时,若能对其进行调整,使其依然保持均匀,则就能有效的保证二叉排序树仍具有较高的查找效率。
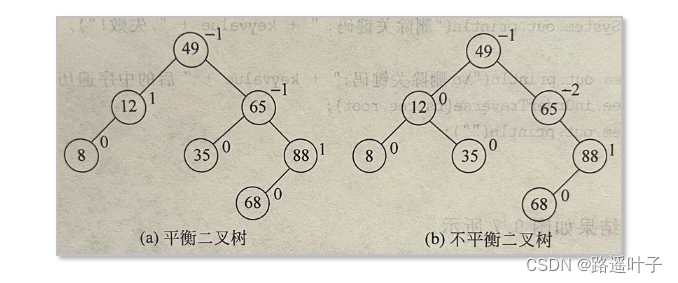
平衡二叉树,是一个特殊的二叉排序树,左右子树分布均匀的二叉排序树。
2)定义
平衡二叉树 Balanced Binary Tree ,又称为AVL树
它或是一棵空树
或是一棵具有下列性质的二叉树:
它的左子树和右子树都是平衡二叉树
且左子树和右子树的深度之差的绝对值不超过1
结点的平衡因子:该结点的左子树深度与右子树深度之差。又称为平衡度。
平衡二叉树也就是树中任意结点的平衡因子的绝对值小于等于1的二叉树。
在AVL树中的结点平衡因子可能有3种取值:-1、0、1。
3)平衡化调整
在平衡二叉树上,插入或删除结点后,可能导致树不平衡,需要通过
旋转让树重新变平衡。失去平衡的二叉树共有
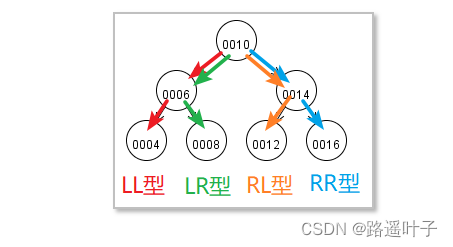
4种旋转方式使其保持平衡:LL型平衡旋转(单向右旋)
RR型平衡旋转(单向左旋)
LR型平衡旋转(先左旋后右旋)
RL型平衡旋转(先右旋后左旋)
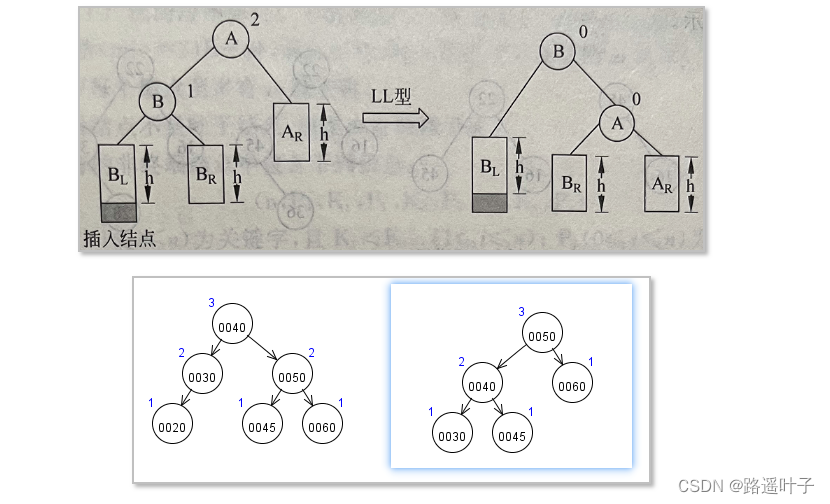
方式1:LL型平衡旋转(单向右旋)
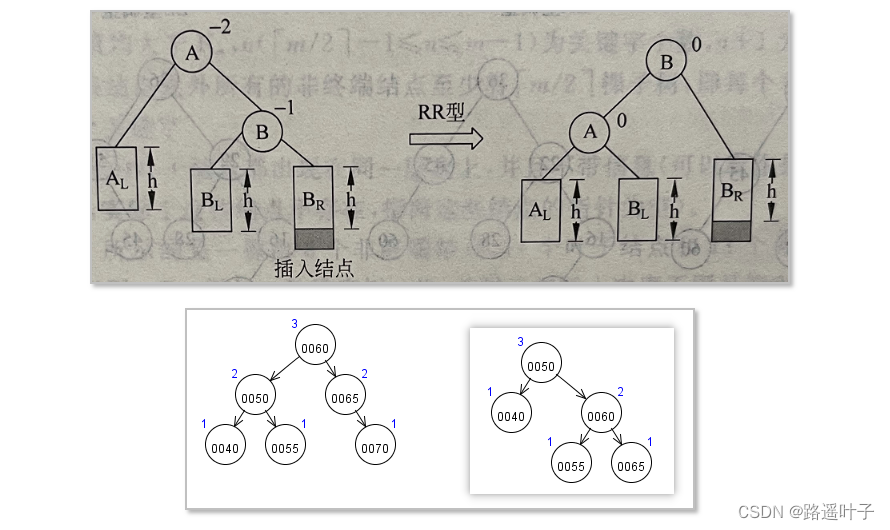
方式2:RR型平衡旋转(单向左旋)
-
方式3:LR型平衡旋转(先左旋后右旋)
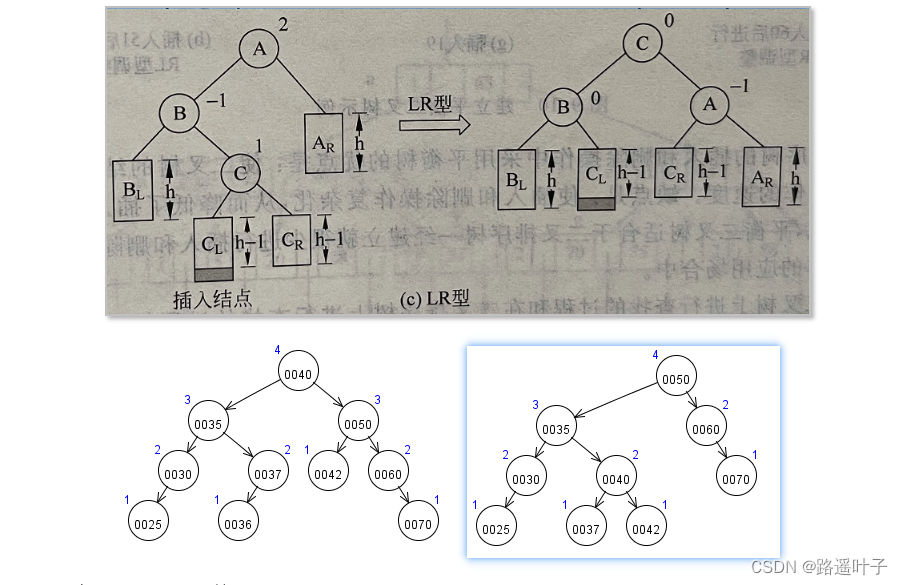
-
方式4:RL型平衡旋转(先右旋后左旋)

4)实例
以关键字 5,4,2,8,6,9 构造一颗平衡二叉树
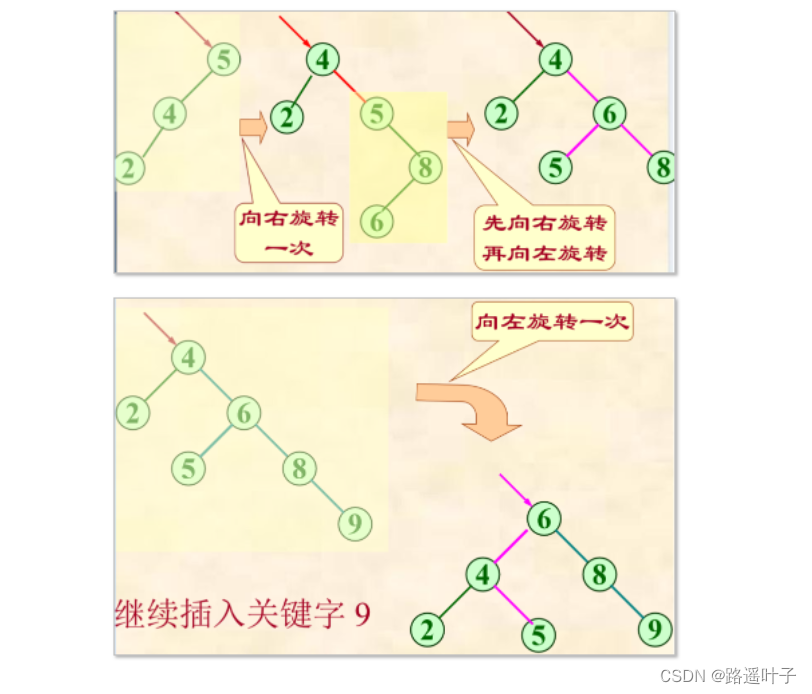
5)性能分析
在平衡树上进行查找的过程和二叉排序树相同,因此,查找过程中和给定值进行比较的关键字的个数不超过平衡树的深度。
平衡二叉树上进行查找的时间复杂度为O(log2n)。
6)练习
练习1:构造一颗平衡二叉树
16, 15, 50, 53, 64, 7
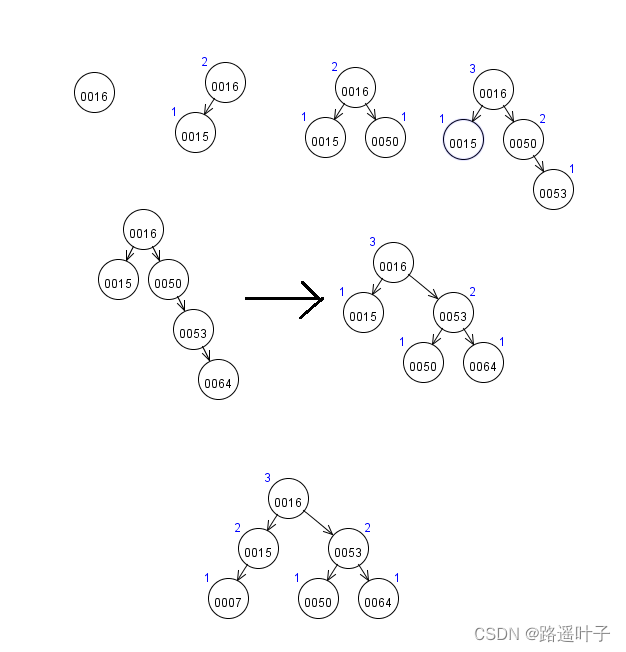
练习2:构造一颗平衡二叉树
2,5,8,3,6,9,1,4,7
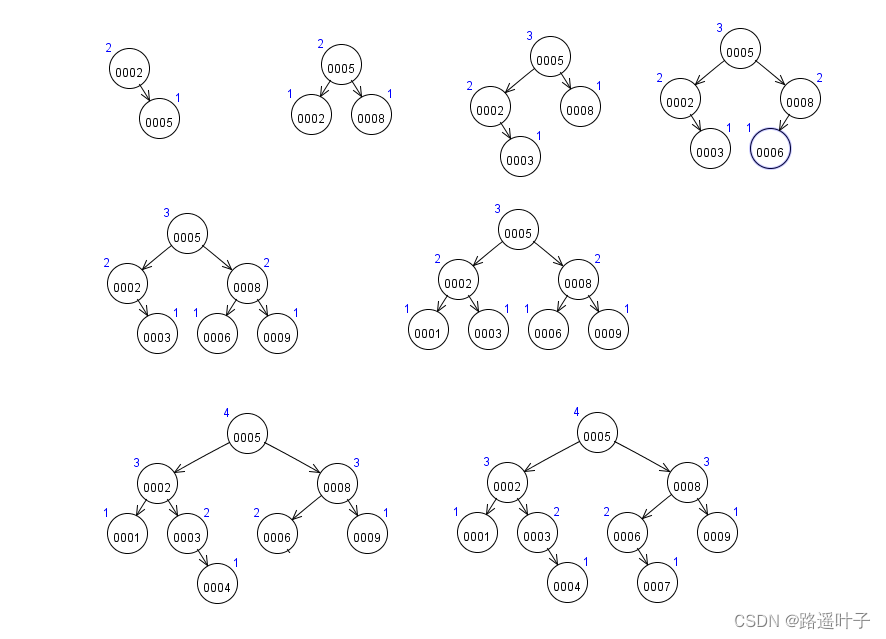
练习3:构造一颗平衡二叉树
1,2,3,4,5,6,7
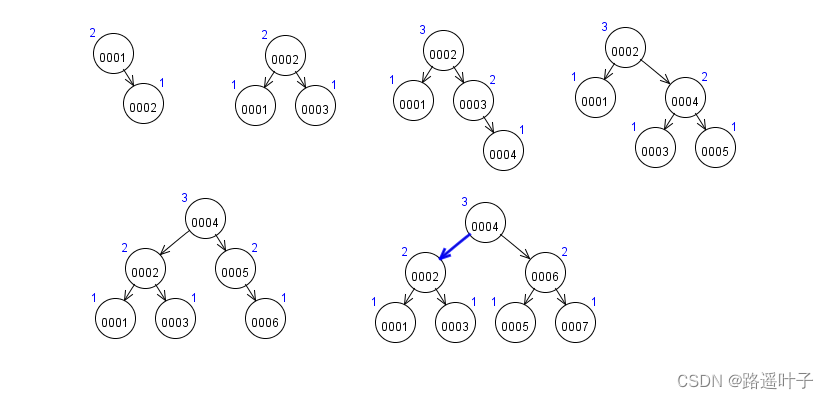
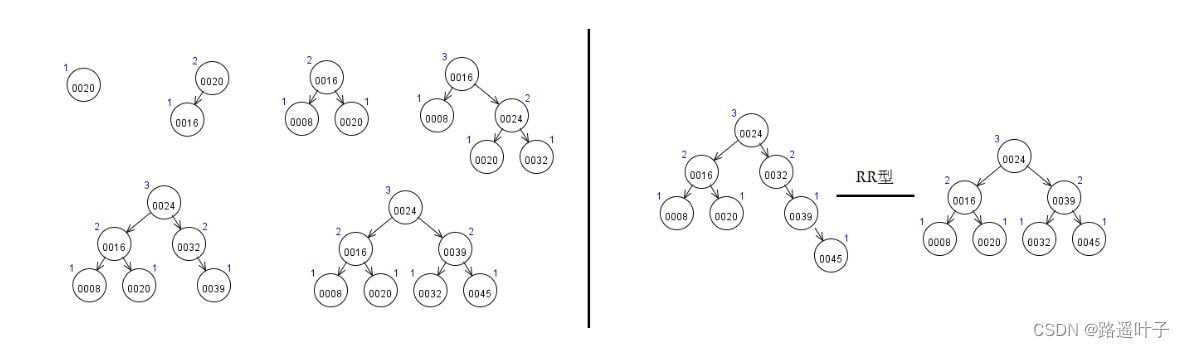
练习4:构造一颗平衡二叉树
20,16,8,32,24,39,45
写到最后
四季轮换,已经数不清凋零了多少, 愿我们往后能向心而行,一路招摇胜!
🐋 你的支持认可是我创作的动力
💟 创作不易,不妨点赞💚评论❤️收藏💙一下
😘 感谢大佬们的支持,欢迎各位前来不吝赐教