目录
前言
冒泡排序法
实现原理:
冒泡排序的基本思想:比较相邻的元素,如果反序则交换。通过第一趟排序能找出最大的元素,并使最大的元素移至最后一位,然后通过第二次排序使次大的元素移至倒数第二位,以此类推,直至所有元素有序。

代码:
#include<iostream>
using namespace std;
void print(int arr[], int n)
{
for(int j= 0; j<n; j++)
{
cout<<arr[j] <<" ";
}
cout<<endl;
}
void BubbleSort(int arr[], int n)
{
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n - i - 1; j++)
{
if (arr[j] > arr[j + 1])
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
int main()
{
int s[10] = {8,1,9,7,2,4,5,6,10,3};
cout<<"初始序列:";
print(s,10);
BubbleSort(s,10);
cout<<"排序结果:";
print(s,10);
system("pause");
} 时间复杂度:

可以得出时间复杂度为:O(N*N)
计数排序
实现原理:
计数排序是一种稳定的排序算法。计数排序使用一个额外的数组C,其中第 i 个元素是待排序数组A中值等于 i 的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它适用于一定范围的整数排序。

代码:
#include <iostream>
#include <vector>
using namespace std;
void CountSort(vector<int> &arr, int maxVal) {
int len = arr.size();
if (len < 1)
return;
vector<int> count(maxVal+1, 0);
vector<int> tmp(arr);
for (auto x : arr)
count[x]++;
for (int i = 1; i <= maxVal; ++i)
count[i] += count[i - 1];
for (int i = len - 1; i >= 0; --i) {
arr[count[tmp[i]] - 1] = tmp[i];
count[tmp[i]]--; //注意这里要减1
}
}
int main()
{
vector<int> arr = { 1,5,3,7,6,2,8,9,4,3,3 };
int maxVal = 9;
CountSort(arr,maxVal);
for (auto x : arr)
cout << x << " ";
cout << endl;
return 0;
}选择排序
实现原理:
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
- 初始状态:无序区为R[1…n],有序区为空;
- 第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1…i-1]和R(i…n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1…i]和R[i+1…n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- n-1趟结束,数组有序化了。
代码:
#include<iostream>
using namespace std;
void select_sort(int* a,int n)
{
for (int i = 0; i < n; i++)
{
int index = i;
for (int j = i + 1; j < n; j++)
{
if (a[index] > a[j])index = j;
}
swap(a[i], a[index]);
}
}
void main()
{
int a[10]{ 5,7,9,6,3,1,4,8 };
select_sort(a, 8);
for (int i = 0; i < 8; i++)
{
cout << a[i]<<" ";
}
}
时间复杂度:
最佳情况:T(n) = O(n2)
最差情况:T(n) = O(n2)
平均情况:T(n) = O(n2)
快速排序
实现原理:
假设我们现在对“6 1 2 7 9 3 4 5 10 8”这个10个数进行排序。首先在这个序列中随便找一个数作为基准数(不要被这个名词吓到了,就是一个用来参照的数,待会你就知道它用来做啥的了)。为了方便,就让第一个数6作为基准数吧。接下来,需要将这个序列中所有比基准数大的数放在6的右边,比基准数小的数放在6的左边,类似下面这种排列。
6 1 2 7 9 3 4 5 10 8 ---------------------------------------------------------> 3 1 2 5 4 6 9 7 10 8
在初始状态下,数字6在序列的第1位。我们的目标是将6挪到序列中间的某个位置,假设这个位置是k。现在就需要寻找这个k,并且以第k位为分界点,左边的数都小于等于6,右边的数都大于等于6。想一想,你有办法可以做到这点吗?
方法其实很简单:分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6的数,再从左往右找一个大于6的数,然后交换他们。这里可以用两个变量i和j,分别指向序列最左边和最右边。我们为这两个变量起个好听的名字“哨兵i”和“哨兵j”。刚开始的时候让哨兵i指向序列的最左边(即i=1),指向数字6。让哨兵j指向序列的最右边(即j=10),指向数字8。
现在基准数6已经归位,它正好处在序列的第6位。此时我们已经将原来的序列,以6为分界点拆分成了两个序列,左边的序列是“3 1 2 5 4”,右边的序列是“9 7 10 8”。
左边的序列是“3 1 2 5 4”。请将这个序列以3为基准数进行调整,使得3左边的数都小于等于3,3右边的数都大于等于3。好了开始动笔吧。
3 1 2 5 4 -------------------------------------------------- -------> 2 1 3 5 4
以此内推将每个数字都排完后哦~
代码:
//快速排序(从小到大)
void quickSort(int left, int right, vector<int>& arr)
{
if(left >= right)
return;
int i, j, base, temp;
i = left, j = right;
base = arr[left]; //取最左边的数为基准数
while (i < j)
{
while (arr[j] >= base && i < j)
j--;
while (arr[i] <= base && i < j)
i++;
if(i < j)
{
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
//基准数归位
arr[left] = arr[i];
arr[i] = base;
quickSort(left, i - 1, arr);//递归左边
quickSort(i + 1, right, arr);//递归右边
}堆排序
实现原理:
什么是堆呀?
堆分为两种:大顶堆和小顶堆,两者的差别主要在于排序方式。
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆;或者每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆。如下图:
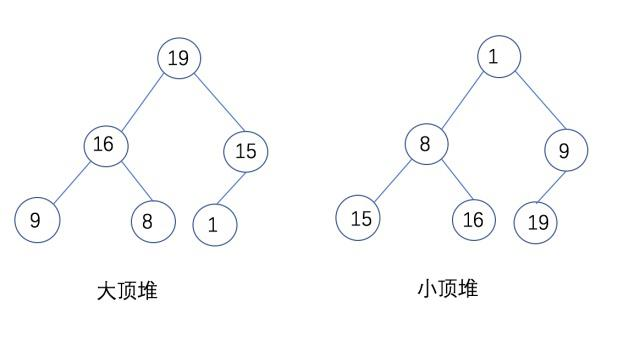
完全二叉树 可以得出添加数据一定得从上往下,从左往右。
堆排序(Heap Sort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。

流程:
先把数组构建成一个大顶堆(父节点大于子节点)
代码:
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
void adjust(int arr[], int len, int index)
{
int left = 2*index + 1;
int right = 2*index + 2;
int maxIdx = index;
if(left<len && arr[left] > arr[maxIdx]) maxIdx = left;
if(right<len && arr[right] > arr[maxIdx]) maxIdx = right; // maxIdx是3个数中最大数的下标
if(maxIdx != index) // 如果maxIdx的值有更新
{
swap(arr[maxIdx], arr[index]);
adjust(arr, len, maxIdx); // 递归调整其他不满足堆性质的部分
}
}
void heapSort(int arr[], int size)
{
for(int i=size/2 - 1; i >= 0; i--) // 对每一个非叶结点进行堆调整(从最后一个非叶结点开始)
{
adjust(arr, size, i);
}
for(int i = size - 1; i >= 1; i--)
{
swap(arr[0], arr[i]); // 将当前最大的放置到数组末尾
adjust(arr, i, 0); // 将未完成排序的部分继续进行堆排序
}
}
int main()
{
int array[8] = {8, 1, 14, 3, 21, 5, 7, 10};
heapSort(array, 8);
for(auto it: array)
{
cout<<it<<endl;
}
return 0;
}