1.概述

狄利克雷分布与贝塔分布、伽马分布有着紧密的联系，在LDA分析中得到了具体应用，本文结合直观理解以及详细的数学推导得到狄利克雷分布，以便加深理解和记录。

2.直观理解

quaro问答网站上有一个举例非常直观，多项分布源于一个投掷骰子，Dirichlet分布是一个骰子工厂。每个样品都是一个称重的，具有相应的多项式分布。如果Dirichlet的参数较大，则模具厂具有较高的精度，并且它生产的所有骰子都将具有接近平均多项式的多项式。如果参数较低，骰子将具有较高的方差（一个骰子可能有很高的概率落在1上，另一个可能有很高的概率落在5上，等等）。极端情况是当参数<1时，方差非常大，pmf集中在角落。

3.

Dirichlet Distribution（狄利克雷分布）与Dirichlet Process（狄利克雷过程）在贝叶斯模型中具有广泛的作用，然而新手对现有的很多材料理解起来可能较为困难，因此我们希望这篇博客能讲清楚相关概念。强烈推荐徐亦达老师在优酷的视频，讲的很清楚，这里我们也借助各种材料来说明一下。
　　Dirichlet Process（狄利克雷过程）是一个随机过程，在非参数贝叶斯模型中有广泛运用，最常见的是作为混合模型的先验。它是一个分布的分布，Dirichlet过程每次样本的抽取都是一个分布。它被称为Dirichlet过程是因为它在有限维上的边缘分布是Dirichlet分布。像高斯分布一样（这是另一个有名的随机过程，用在贝叶斯回归中，可参考机器学习中的高斯过程），它的有限维边缘分布是高斯分布。从Dirichlet过程中抽取的分布是离散的，但无法使用有限个参数描述，因此它被归为非参数模型。
　　一个简单的例子
　　我们知道，在混合模型中，我们假设有观测量\{x_1,x_2,...,x_n\}{x​1​​,x​2​​,...,x​n​​}，它们分别来自参数为\{\theta_i|i=1,2,...,n\}{θ​i​​∣i=1,2,...,n}的分布（注意每个数据点来自一个分布，其参数为\thetaθ，那么同一个分布的参数是一样的，也就是说必然存在很多\thetaθ是相等的）。在贝叶斯方法中，我们需要假设这n个\thetaθ是来自于某个分布中。注意，如果我们假设\thetaθ是来自一个连续的分布，也就是说模型的先验分布假设是一个连续分布的话，那么没有哪两个\thetaθ的值是一样的。因为连续分布的样本不可能有一样的。这显然不符合混合模型的要求。如何解决这个问题呢？我们可以使用Dirichlet Process（狄利克雷过程）作为先验解决这个问题。假设，\theta \sim Hθ∼H，H可以是连续分布，也可以不是。那么我们可以考虑构造一个离散的分布GG，使\thetaθ来自于GG来解决这个问题。那么这里我们肯定需要使GG和HH很相似，这样我们才能使用GG中抽取的\thetaθ。在这里，我们可以定义GG是来自基分布为HH的Dirichlet Process（狄利克雷过程）来解决这个问题。
　　在说明Dirichlet Process（狄利克雷过程）之前，我们需要了解一下Dirichlet Distribution（狄利克雷分布），它是Beta分布在多元上的推广，其参数是一个实数向量（比如m个\alphaα），它的一个样本就是一个多元向量（比如m个\thetaθ），它是多项式分布的共轭先验。这篇博客将首先简要介绍一下贝叶斯非参数模型，然后介绍Dirichlet Distribution（狄利克雷分布），接下来将重点说明Dirichlet Process（狄利克雷过程）及其应用。理解Dirichlet Process（狄利克雷过程）需要我们了解测度（measure）的基本概念，因此我们在第三小节中将简要介绍一下这个概念。

3.详细推导

维度K ≥ 2的狄利克雷分布在参数α1, ..., αK > 0上、基于欧几里得空间RK-1里的勒贝格测度有个概率密度函数，定义为：

,

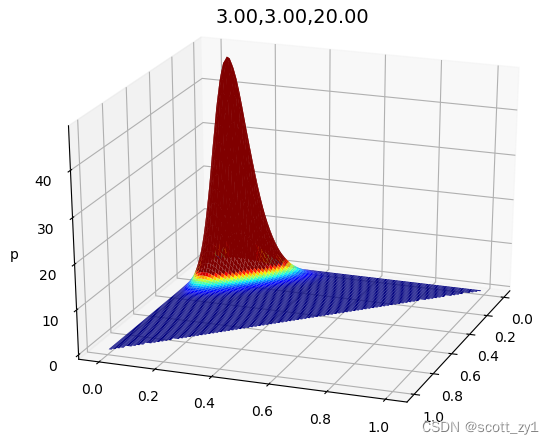
4. 实现效果

                        ​​​​​​​

        ​​​​​​​        ​​​​​​​

5.应用举例