目录

一、二叉树的建立

二、二叉树的遍历

三、例题

一、二叉树的建立

以二叉树作为存储结构，按先序遍历序列建立二叉树：

依据先序遍历的递归过程生成结点，建立二叉树的二叉链表，因此生成二叉树算法也是递归的。例如，按照ABC##DE#G##F###的顺序依次读入字符可以建立该二叉树的二叉链表。创建过程中，遇到#表示空树。递归生成过程如下：

（1）读入A，创建根结点A。

（2）先序遍历创建A的左子树，读入B，创建结点B，B为A的左孩子。

（3）先序遍历创建B的左子树，读入C，创建结点C，C为B的左孩子。

（4）先序遍历创建C的左子树，读入#，C的左子树为空。

（5）先序遍历创建C的右子树，读入#，C的右子树为空；B的左子树创建完毕。

（6）先序遍历创建B的右子树，读入D，创建结点D，D为B的右孩子。

依次继续创建D的左右子树，直至全部数据读入完，二叉链表建立结束。

先序遍历创建二叉树算法如下： 

void createBiTree(BiTree *t){
	char s;
	scanf("%c",&s);
	getchar();
	BiTree q;
	if(s=='#'){
		*t=NULL;
		return ;
	}
	q=(BiTree)malloc(sizeof(BitNode));    //创建根结点
	q->data=s;
	*t=q;
	createBiTree(&q->lchild);
	createBiTree(&q->rchild);
}

二、二叉树的遍历

二叉树的三种遍历方法具体见下：

https://blog.csdn.net/m0_68111267/article/details/127456948?spm=1001.2014.3001.5502 

三、例题

【问题描述】

以二叉链表的形式创建二叉树（不超过20个结点），并编写二叉树的遍历算法，实现二叉树的三种遍历。

【输入形式】

输入二叉树的结点信息（以先序建立的方式）。

【输出形式】

输出二叉树的三种遍历序列。

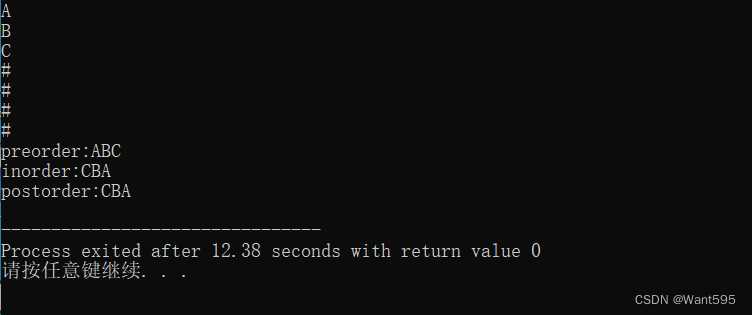
【样例输入1】

A

B

C

#

#

#

#
【样例输出1】

preorder:ABC

inorder:CBA

postorder:CBA

【样例输入2】

A

B

#

#

C

#

#
【样例输出2】

preorder:ABC

inorder:BAC

postorder:BCA

#include<stdio.h>
#include<malloc.h>
typedef struct BitNode{
	char data;
	struct BitNode *lchild,*rchild;
}BitNode,*BiTree;
void createBiTree(BiTree *t){
	char s;
	scanf("%c",&s);
	getchar();
	BiTree q;
	if(s=='#'){
		*t=NULL;
		return ;
	}
	q=(BiTree)malloc(sizeof(BitNode));
	q->data=s;
	*t=q;
	createBiTree(&q->lchild);
	createBiTree(&q->rchild);
}
void preorder(BiTree t){
	if(t!=NULL){
		printf("%c",t->data);
		preorder(t->lchild);
		preorder(t->rchild);
	}
}
void inorder(BiTree t){
	if(t!=NULL){
		inorder(t->lchild);
		printf("%c",t->data);
		inorder(t->rchild);
	}
}
void postorder(BiTree t){
	if(t!=NULL){
		postorder(t->lchild);
		postorder(t->rchild);
		printf("%c",t->data);
	}
}
int main(){
	BiTree t;
	createBiTree(&t);
	printf("preorder:");
	preorder(t);
	printf("\ninorder:");
	inorder(t);
	printf("\npostorder:");
	postorder(t);
	printf("\n");
	return 0;
}