主要学习目标

我们主要的学习目的是简单看一遍西瓜书里面的内容,尽可能的对各个模型都有一定的了解,在本节课程当中,我会给大家分享机器学习相关的的内容,我主要是在学习吴恩达老师最新的机器学习的视频,但是学完之后还是觉得较为空泛,所以在此,借机会再重新复习
在这里插入图片描述

神经网络

什么是神经网络?
从最一开始的输入层之后,神经网络中的每个神经元节点接受上一层神经元的输出值作为本神经元的输入值，并将输入值传递给下一层，输入层神经元节点会将输入属性值直接传递给下一层（隐藏层或输出层)。
在多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数。
简单来说，激活函数，并不是去激活什么，而是指如何把激活的神经元的特征通过函数把特征保留并映射出来，即负责将神经元的输入映射到输出端。

神经元模型

神经元的模型可以简单的理解为神经元对于传入的信息通过我这个神经元自身的一个理解去尝试对传入的信息做一定的调整然后作为该神经元的输出值然后作为下一个神经元的输入值再传入
在机器学习当中使用到的神经元被称为激活函数
下面简单介绍一下常见的激活函数

激活函数

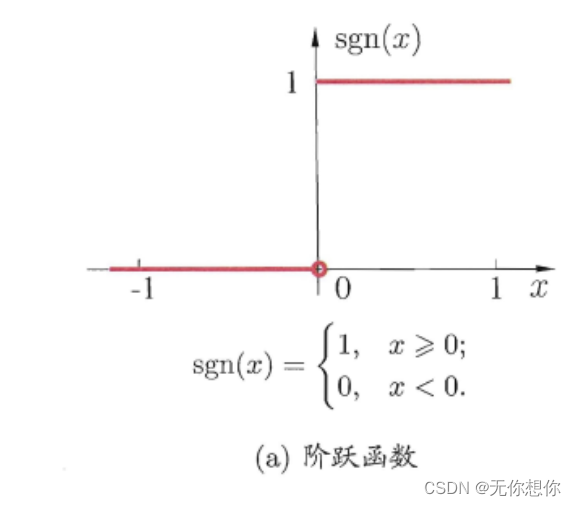
阶跃函数

$y=\operatorname{sgn}\left(\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}-\theta\right)=\left\{\begin{array}{ll} 1, & \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}-\theta \geqslant 0 \\ 0, & \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}-\theta<0 \end{array}\right.$
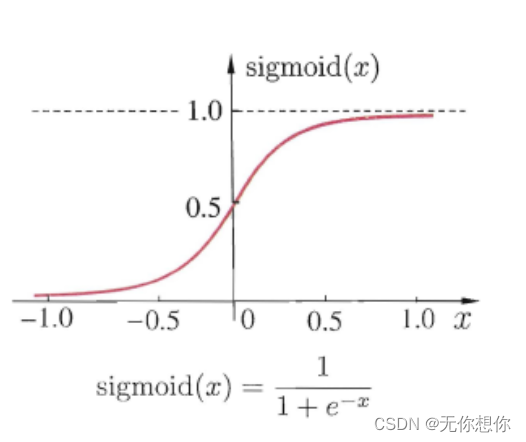
在这里插入图片描述

Sigmoid函数

为解决阶跃函数的不连续性,Sigmoid也是一个很好的激活函数
$\operatorname{sigmoid}(x)=\frac{1}{1+e^{-x}}$
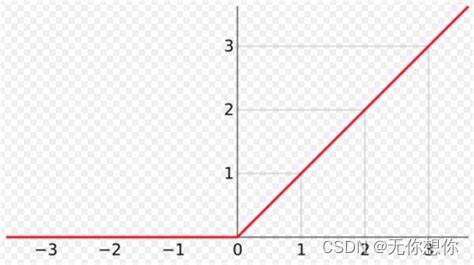
在这里插入图片描述

ReLU函数

西瓜书上没有提及,但是经常用到的就是ReLU函数,由于Sigmoid函数存在的问题是要进行一个 $e$ 的计算,指数计算对于很多问题当中都是十分贵的,所以为了尽可能的避免这样的消耗,所以ReLU也是一个常用的方法,也是个人认为相较来说最好的方法
(图片网上找到的,水印不知道怎么删)
在这里插入图片描述

感知机与多层网络

在神经网络当中输入层和输出层之间还有隐藏层(被称为隐层)
感知机可以理解为只有单层的网络,一般用于解决线性的数据集,但是如果是非线性的,就不能实现分类了,那么就需要提出多层感知机
常用的错层网络为多层前馈神经网络,其所拥有的特点就在于

每层神经元与下一层完全互连
不存在同层链接
不存在跨层链接

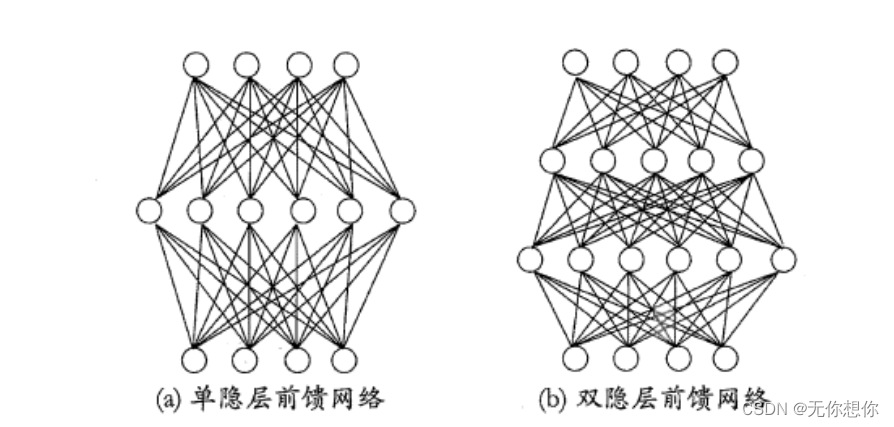
输入层神经元仅接受输入,但是隐层和输出层则包含功能神经元,会对输入值进行函数处理

BP神经网络

BP神经网络可以说是目前最优秀的神经网络算法,其适用范围十分广阔
在这里插入图片描述

BP神经网络的目标

BP算法的目标要最小化训练集 $D$ 上的累积误差
$E=\frac{1}{m}\sum_{k=1}^{m}$

全局最小和局部极小

在神经网络的运用当中,遇到过拟合和欠拟合都是一件十分令人头疼的事情,我们在使用BP神经网络这类方法的时候也容易遇到局部最优解,虽然说对于一些简单的函数比如 $y=x^2$ 这样的函数可以找到全局最优解,但是对于多元函数,例如下面这张图
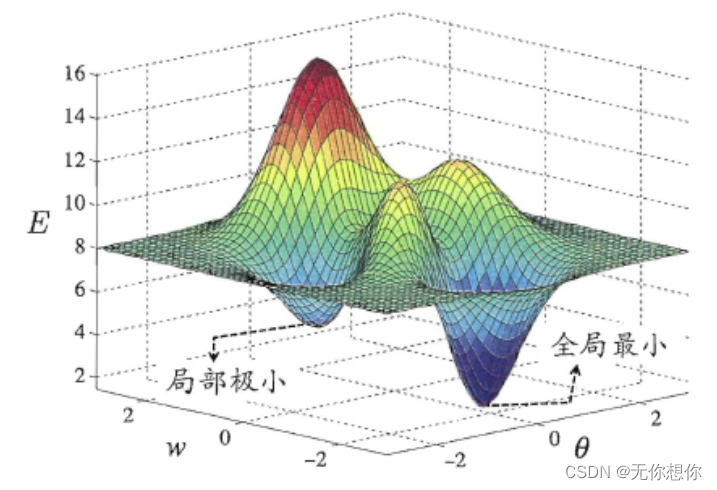
在这里插入图片描述
我们使用神经网络的时候就十分容易陷入局部最优解,所以也提出了一定的方法来避免这种情况

模拟退火算法
随机梯度下降

深度学习

深度学习可以理解为是一种特征学习,就是通过多个隐藏层来把输入信号进行逐层加工,通过多层处理,实现初始的低层特征表示转化为高层特征表示,使用简单模型完成复杂任务的学习

总结

在本次课程当中我们学习并了解到了机器学习的,让我们继续努力

西瓜书之神经网络