NLLLoss

• 假设我现在做 NLP 任务，在不考虑 batch 大小的前提下：

  • 词表大小 vocab_size = 3 {0: 我, 1:吃, 2:饭}
  • 句子的长度 seq_len = 2
  • 那么现在我得到了一个张量，维度是 $(Vocab\_size,seq\_len)$ (3,2)，三行两列，每一列是一个列向量代表句子中的一个词的 logits 分布:

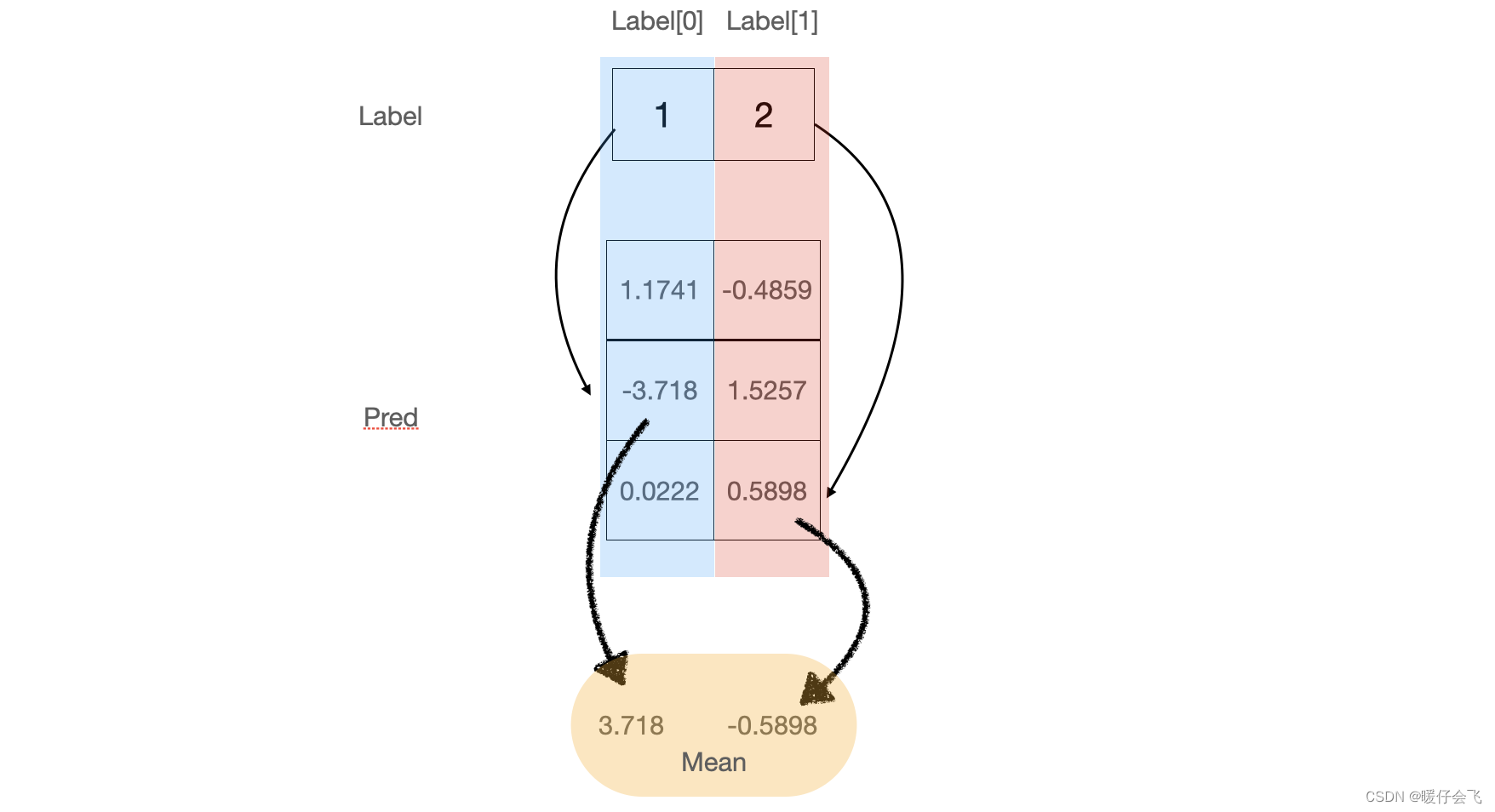
  tensor([[ 1.1741, -0.4859],
          [ -3.7180,  1.5257],
          [ 0.0222,  0.5898]])
  

  • label 是：

  tensor([1, 2])
  

  这里先插一句在当前情境下 NLLOSS 的计算规则：

  • 第一步：将 label 中的每个值，作为 predict 结果中对应列的索引值，拿到 predict 对应列中的具体值，在这里就是在第一列中取出 -3.718，第二列中取出 0.5898
  • 第二步：将这些取出的值取反，得到 3.718，-0.5898
  • 第三步：将这些取反后的值进行相加 (3.718-0.5898) / 2=1.5641

  pred = torch.tensor([[ 1.1741, -0.4859],
      [ -3.718,  1.5257],
      [ 0.0222,  0.5898]], dtype=torch.float32)
  label = torch.tensor([1,2], dtype=torch.long)
  # 先忽略这里的 ignore_index 后面会讲
  loss = NLLLoss(ignore_index=3)
  # 由于用 NLLLoss 计算的时候必须要有 batch 的维度，所以我们暂且迎合这个规则，增加一个 batch维度
  loss(pred.unsqueeze_(0), label.unsqueeze_(0))
  

  • 目前 label 给出的信息，这两个字应该是 ['吃', '饭']
  • 但模型的预测结果并不这么觉得，首先看 第一列 的分布

    tensor([1.1741, -3.7180, 0.0222])
    

  • 这个分布就表明了，对于预测结果的第一个词的预测过程，词表中的 index=0 （我）的词的和 index=3（饭）都做了有利的贡献（分布中的对应值>0），而词表中 index=1 的词（吃）做了反向的贡献
  • 在 NLLloss 计算的时候，恰好在第一列中把 -3.718 这个数取出来了（label[0]=1)，而这个词是一个做了反向贡献的词，所以 loss 值就变成了 3.718. 而如果 label[0] = 0 则取出来的是 1.1741 这个值，那么经过 NLLloss 计算后，这个一列的 loss 会变成 -1.1741，也就是 loss 为负值，loss越小当然越好。
    
  • 那么为什么把 label 的值当做 pred 结果中此列的索引的这种计算方式能够反映当前模型学习的效果呢？即为什么 NLLloss 是有效的：

  • 我们假设如果这个模型学的非常好，那么当 label = 1 的时候，理应第一个列的 logits 分布中index=1 的位置就应该是一个较大的正值。如果他是个负值或者比较小的正值，就代表模型学的不够好。

CrossEntropy

• 与 NLLLoss 的情景一样，我们依然沿用刚才的 pred 和 label

  	tensor([[ 1.1741, -0.4859],
  	        [ -3.7180,  1.5257],
  	        [ 0.0222,  0.5898]])
  

  • label 是：

    tensor([1, 2])
    

  • 还是先介绍 CrossEntropy 的计算步骤：

    • 第一步：按照列进行 softmax 操作，pred 首先变成了：

    pred = torch.tensor([[ 1.1741, -0.4859],
            [ -3.718,  1.5257],
            [ 0.0222,  0.5898]], dtype=torch.float32)
    label = torch.tensor([1,2], dtype=torch.long)
    s = F.softmax(pred, dim=0)
    print(s)
    tensor(
    	[[0.7555, 0.0877],
        [0.0057, 0.6553],
        [0.2388, 0.2570]])
    

    • 第二步：对当前的这个矩阵逐点计算 log 值

    torch.log(s)
    tensor([[-0.2803, -2.4343],
            [-5.1724, -0.4227],
            [-1.4322, -1.3586]])
    

    • 第三步：对当前的这个矩阵计算 NLLloss

    [-(-5.1724) + -(-1.3586)] / 2 = 3.2655
    

  • 那么为什么 CrossEntropy 有效呢？

    • 首先 softmax 的操作让每一列分布的差异变得更大
    • 由于 softmax 会让某一列的值分布在 0-1 之间，所以我们通过 log 计算之后，所有的值都 < 0，从第一列的值的变化就可以看出，原本的 -3.718 再进行了 softmax 和 log 运算之后被扩大成了 -5.1734，而原本不明显的 0.222 也被拉大到了 -1.4322。因为 softmax 的特点是将一个负数变成一个非常贴近 0 的正数，而 log 的作用又会将贴近 0 的值变成一个很大的负数。很显然这一套操作下来（softmax + log)，除了原本比较大的正值，那些原本 0 附近的正值和所有的负值造成的损失值都会变大很多。这样就避免了模型学习的时候 label 对他模棱两可的指导。比较小的正值也会产生 loss 来惩罚模型，从而帮助模型尽可能给出比较大的正值。
    • 使用 softmax 同时还有一个好处：那就是在同一个句子中，不管是预测的结果是对的还是错的，都会产生 loss 值，因为所有的位置在 log 之后都是负值，而再经过 NLLLoss 都会变成正值。这样就避免了某个词的 loss 是负数和其他词的 loss 取平均的时候将 loss 给抵消掉的问题。

联系

• 从上面的例子中，我们也可以看出来：

  CrossentropyLoss = Softmax + log + NLLLoss