目录

1.什么是递归

2.最简单的递归

3递归的必要条件

4递归输出一个数的每位之和

5 n的阶乘的递归

6.斐波那契数列的递归

7递归的优缺点

河大大一新生一枚

喜欢计算机；喜欢编程；

目前再学习C的过程中，会定时分享自己学习过程中的心得

希望和大家一起学习，也希望大家多多关注

 1.什么是递归

要想要学会递归，必须先明白什么事递归。简单用代码说来是函数调用本身的过程。

把一个很大的问题。抽象出与其相似的子问题。再把子问题抽象成一个更小的子问题。

层层递归。最问题简化成我们常见的最简单的形式

2.最简单的递归

 请大家看看这几行代码。想一下输出结果是什么；

下面由我这个小菜鸡给大家分析一下。首先我们写了一个test()函数。这个函数的功能

是什么呢？是打印一段话。打印完之后我们又在test函数中调用了本身。并在main函数

中调用了test。就相当与这个test函数会不断的重复运行。那结果是什么呢？答案是会

一直输出“河大很美丽"直到程序出现栈溢出。

下面简单解释一下什么是栈溢出

内存四区：

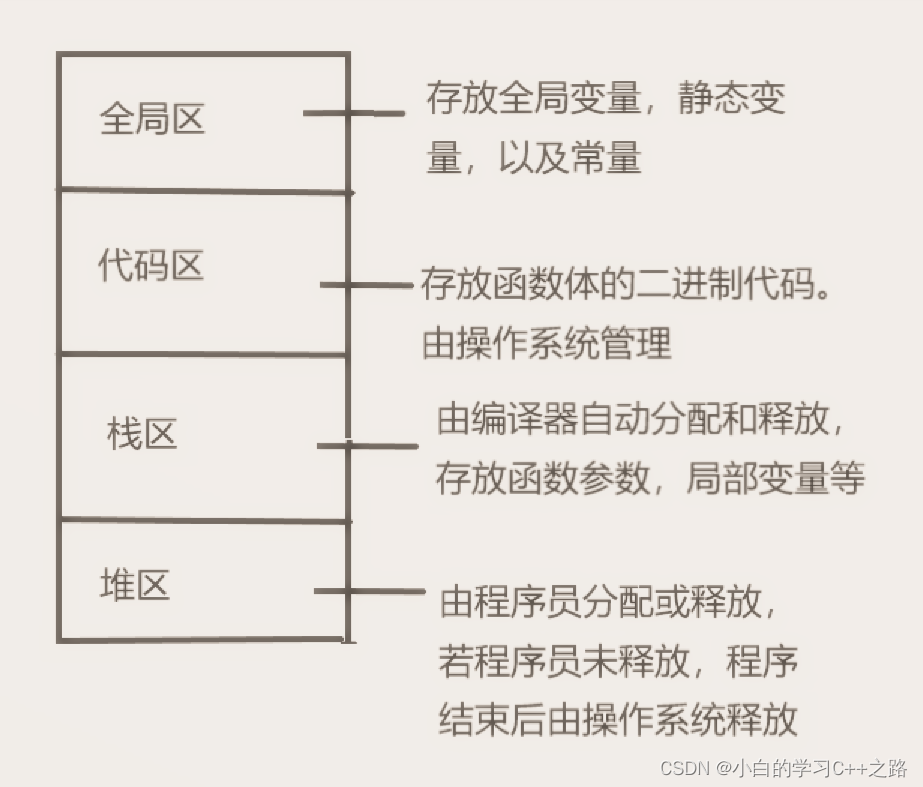
 大家可以简单浏览一下内存分区模型

这里只研究栈区。每次调用函数。都会向栈区申请一部分空间用于存放函数参数，等信息；

在上述代码中函数不断的调用。不断的向栈区申请空间。没有终止条件。栈区的空间迟早会被

申请满。这时候就会造成栈溢出。大家明白了吗？

上面这行代码只是简单的让大家体验一下函数调用函数是怎么一回事；但他并不是一个

真正的递归。下面将会介绍为什么不是真正的递归；

3.递归的必须条件

 由上面的栈溢出可知，要想实现递归必须存在终止条件；下面重点讲讲这个；

宝子们，划重点哦；

由上面的分析相信大家对递归有了基本的了解

1.递归必须存在限制条件，当满足这个限制条件时候，递归必须停止

2.每次递归的过程中必须越来越接近这个限制条件

可以给大家画一下图解释一下

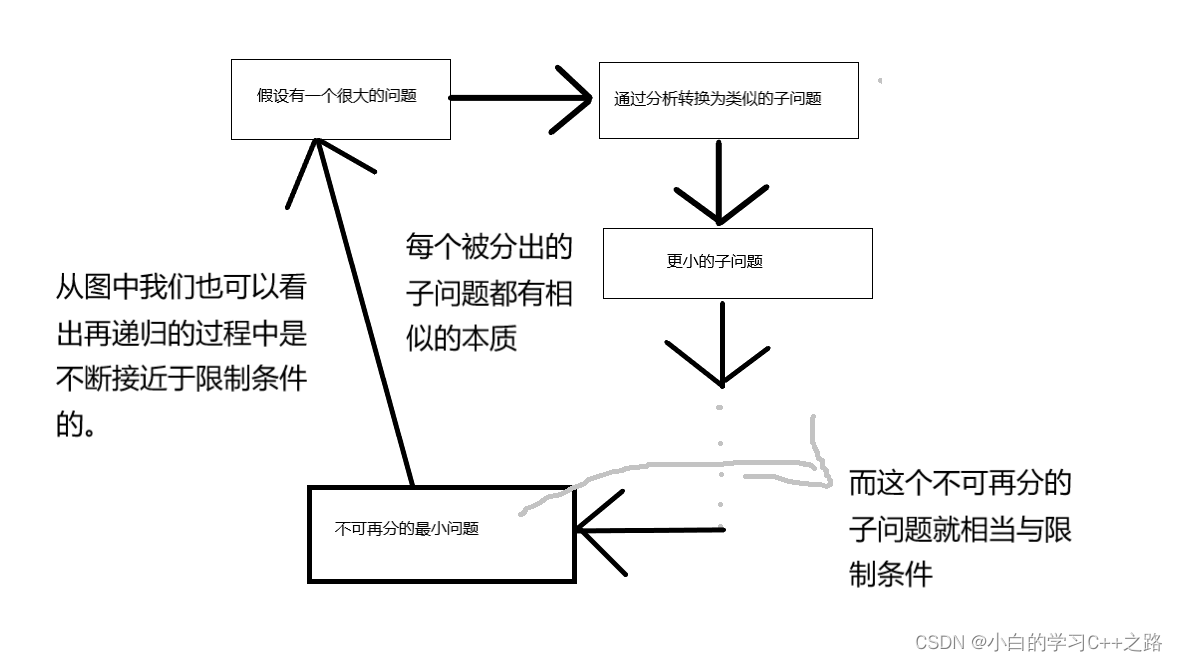
 哈哈，相信大家通过这个图已经能很清楚的明白了递归的俩个条件。

 下面举几个例子吧

1.递归循环输出一个数的每一位之和

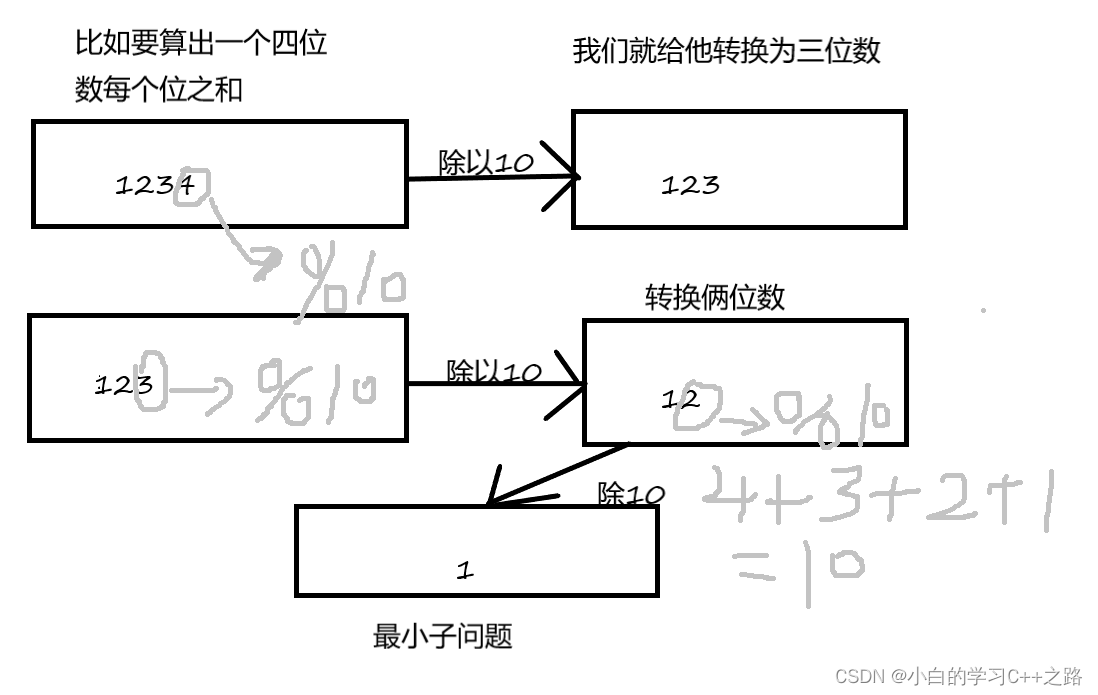
 看到这里相信大家都明白怎么回事了。案例上代码。

 2计算n的阶乘的问题

 3.斐波那契数列的递归

这里要先了解斐波那契数列是什么和其递推公式

1，1，2，3，5，8，........f(n) = f(n-1)+f(n-2);

知道这个递推公式后问题就会变得很简单

 小结，分解大问题为简单小问题，划不开，有没有递推公式？有没有等价

的式子呢？

一定要注意 递归的俩个条件

递归的优点：简单，思路好想，容易求解答案

缺点：需要计算的式子很多很多，容易栈溢出，时间复杂度非常高；

拿上面的斐波那契数的求法举例；

很不幸，这个代码的效率低到难以想象

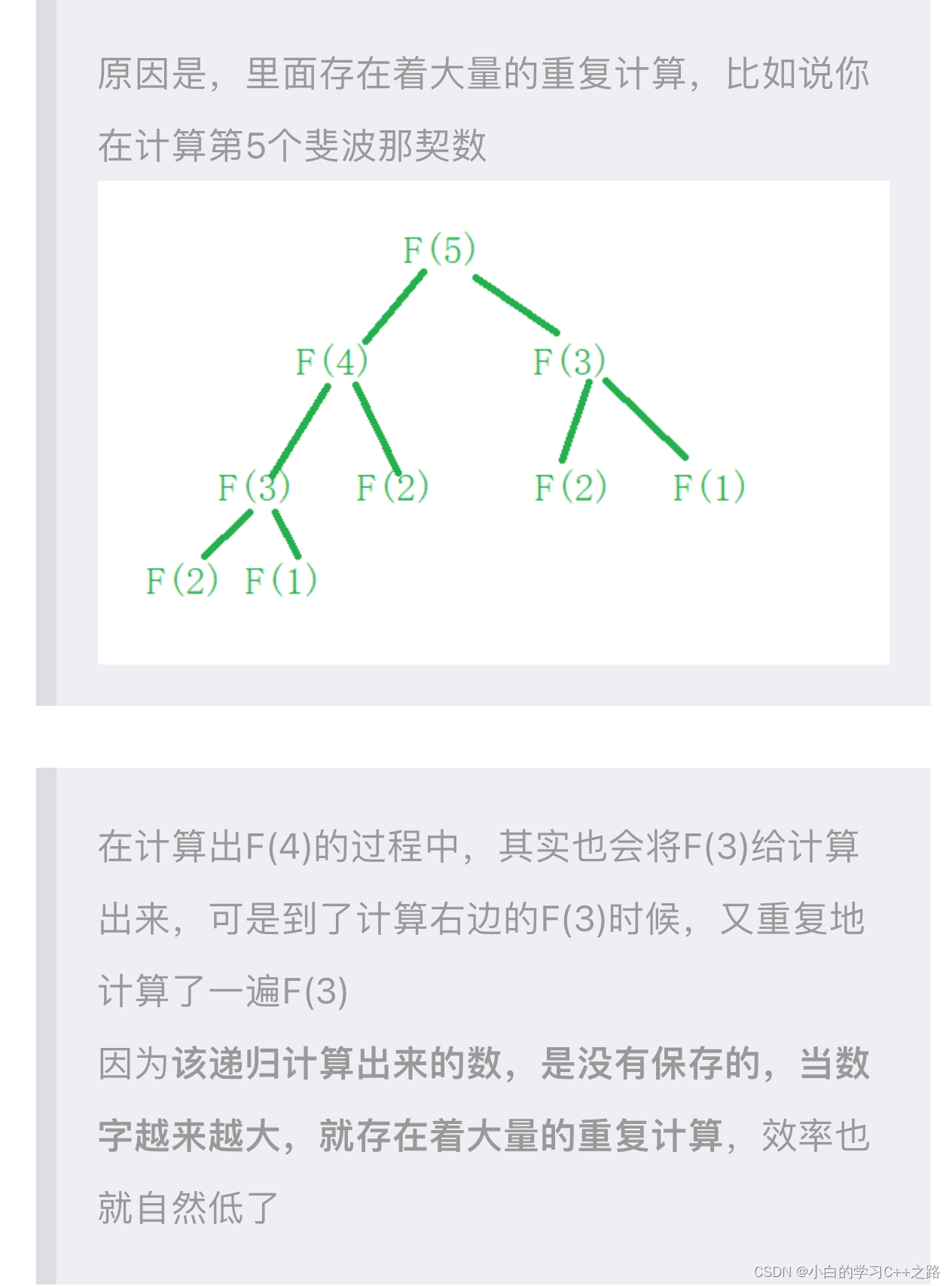
 这样并不直观，计算30！我们可以计算一下第四个斐波那契数被计算了多少次

 大家猜一下运行结果，绝对想不到

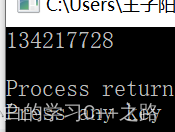
 竟然有这么多次，可见效率之低

所以当大家再写代码的时候，能用循环的尽量少用递归。

最后送大家一张图，可以帮助理解递归

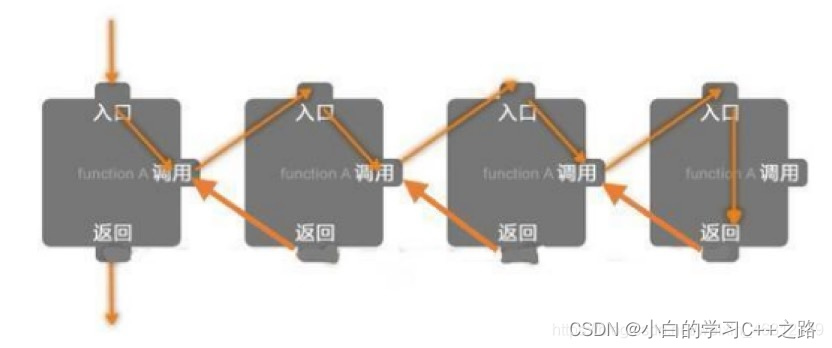
动大脑思考找到最优解是每个程序员的追求

本章到这里就结束了，建议大家多画图多理解，当然大家都是小白，这只是我对

递推的浅层次看法。路还很长。理解会不断提升。

希望能帮助到学习路上的问题

下一期将会出小实战—汉诺塔问题和青蛙跳台问题，以及对斐波那契数列求法的优化

希望大家可以关注哦；

创作不易，还请一键三连。不要下次一定哦