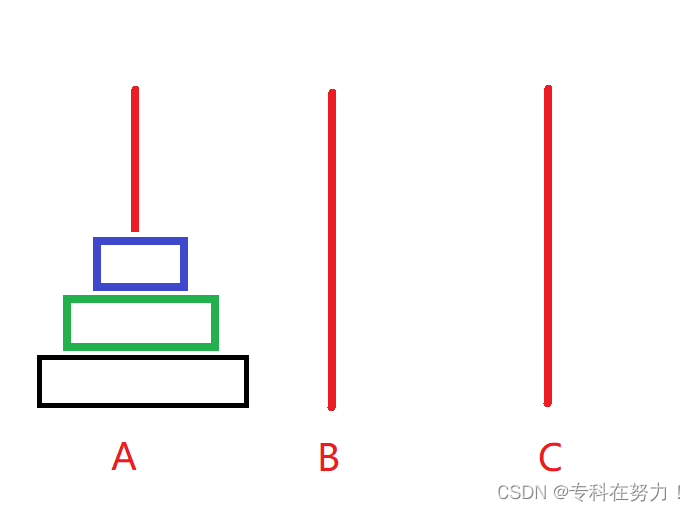
汉诺塔问题

该问题的主要材料包括三根高度相同的柱子和一些大小及颜色不同的圆盘，三根柱子分别为起始柱A、辅助柱B及目标柱C
将A柱上的盘子全部移到B柱上
操作规则: 每次只能移动一个盘子,小盘子可以放在大盘子上面，大盘子不可以放在小盘子上面

如果大家对汉诺塔问题不是特别了解，可以去微信的小程序去玩一下，有助于大家对问题的了解
既然是解题，那我们要用最少的步骤来完成它
下图就是最佳解法

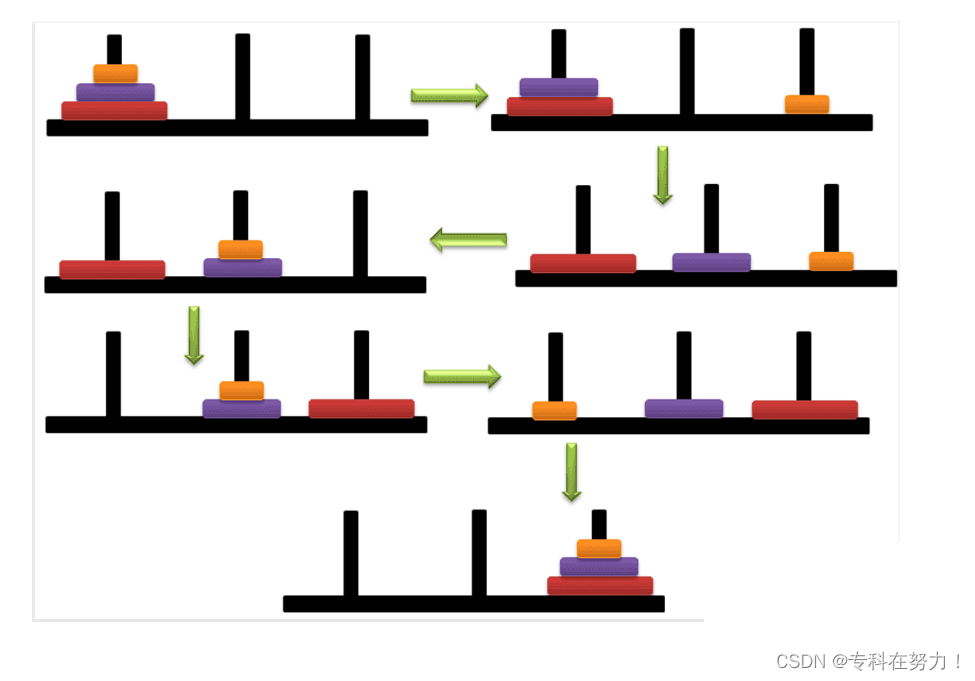
方法：
1.我们先借助C柱把A柱上n-1个盘子，移到B柱上
2.再把A柱上最大的盘子放在C柱上
3.B柱上的n-1个盘子借助A移到C柱

——————————————————————
我们有递归思路来求解这道题就简单了
先来看代码，我会在代码中写注释加以解释

#include<stdio.h>

void move(char A, char C, int n)
{
	//打印每次是怎样移动的
	printf("把第%d个圆盘从%c--->%c\n", n, A, C);
}

void HanoiTower(char A, char B, char C, int n)
{
	//当就剩一个盘子的时候直接移到C柱上 
	if (n == 1)
	{
		move(A, C, n);
	}
	else
	{
		//将n-1个盘子从A柱借助于C柱移动到B柱上
		HanoiTower(A, C, B, n - 1);
		//将A柱子最后一个盘子移动到C柱上
		move(A, C, n);
		//将n-1个盘字从B柱借助于A柱移动到C柱上
		HanoiTower(B, A, C, n - 1);
	}
}

int main()
{
	int n = 0;
	printf("输入A柱子上的圆盘个数：");
	scanf("%d", &n);
	//将n个盘子从A柱借助于B柱移动到C柱上
	HanoiTower('A', 'B', 'C', n);
	return 0;
}

这里大家最容易混的点应该就是函数的参数了

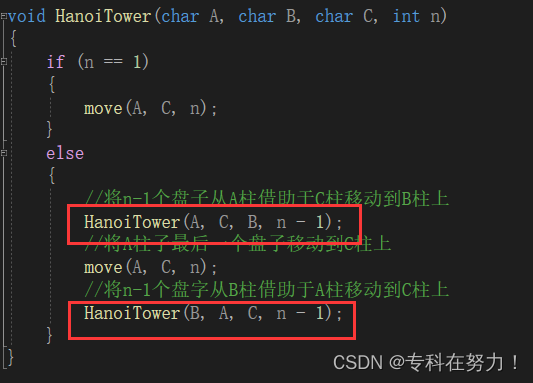
可能会想：这里每次传参都是与函数的接收参数不符合，程序不会出错吗？
这里大家与要注意的是我们接收参数的是变量名并不是参数本身
这里我专门为大家做了解析图

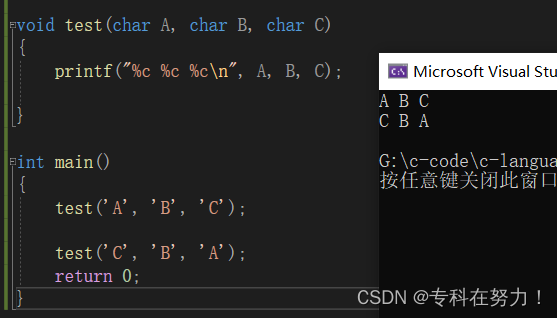
所以我们每次传递的都是 ‘A’, ‘B’, 'C’而不是变量名，别在这里搞混了

当n=1时：
1.将A柱上最后一个圆盘移动到C柱上（A →C）

当n=2时：
1.将1个圆盘从A柱移动到B柱上，重复n=1时的步骤，只不过是将那1个圆盘（从A借助于B移动到C）改为（从A借助于C移动到B）
2.将A柱上最后一个圆盘移动到C柱上（A →C）
3.将B柱上的1个圆盘移动到C柱上。重复n=1时的步骤，只不过是将那个圆盘（从A借助于B移动到C）改为（从B借助于A移动到C）

当n=3时：
1.将2个圆盘从A柱移动到B柱上。重复n=2时的步骤，只不过是将那2个圆盘（从A借助于B移动到C）改为（从A借助于C移动到B）
2.将A柱上最后一个圆盘移动到C柱上（A →C）
3.将B柱上的2个圆盘移动到C柱上。重复n=2时的步骤，只不过是将那2个圆盘（从A借助于B移动到C）改为（从B借助于A移动到C）

当n=4时：
1.将3个圆盘从A柱移动到B柱上。重复n=3时的步骤，只不过是将那3个圆盘（从A借助于B移动到C）改为（从A借助于C移动到B）
2.将A柱上最后一个圆盘移动到C柱上（A →C）
3.将B柱上的3个圆盘移动到C柱上。重复n=3时的步骤，只不过是将那3个圆盘（从A借助于B移动到C）改为（从B借助于A移动到C）

如果还是不理解建议大家画一下图感受一下

！！！当时我就是这里混了

如果大家对形参和实参区分不是特别了解可以看一下我博客中的函数讲解那一章，里面有对形参与实参的讲解