由唯一性定理导出的另一个常用的方法是电轴法。可用它求解的基本系统是两个平行的无限长带电圆柱导体，这两根导体圆柱在单位长度上所带的电荷量相等而符号相反。
目录
1.两根相互平行且带电量异号电荷的无限长直导线的场
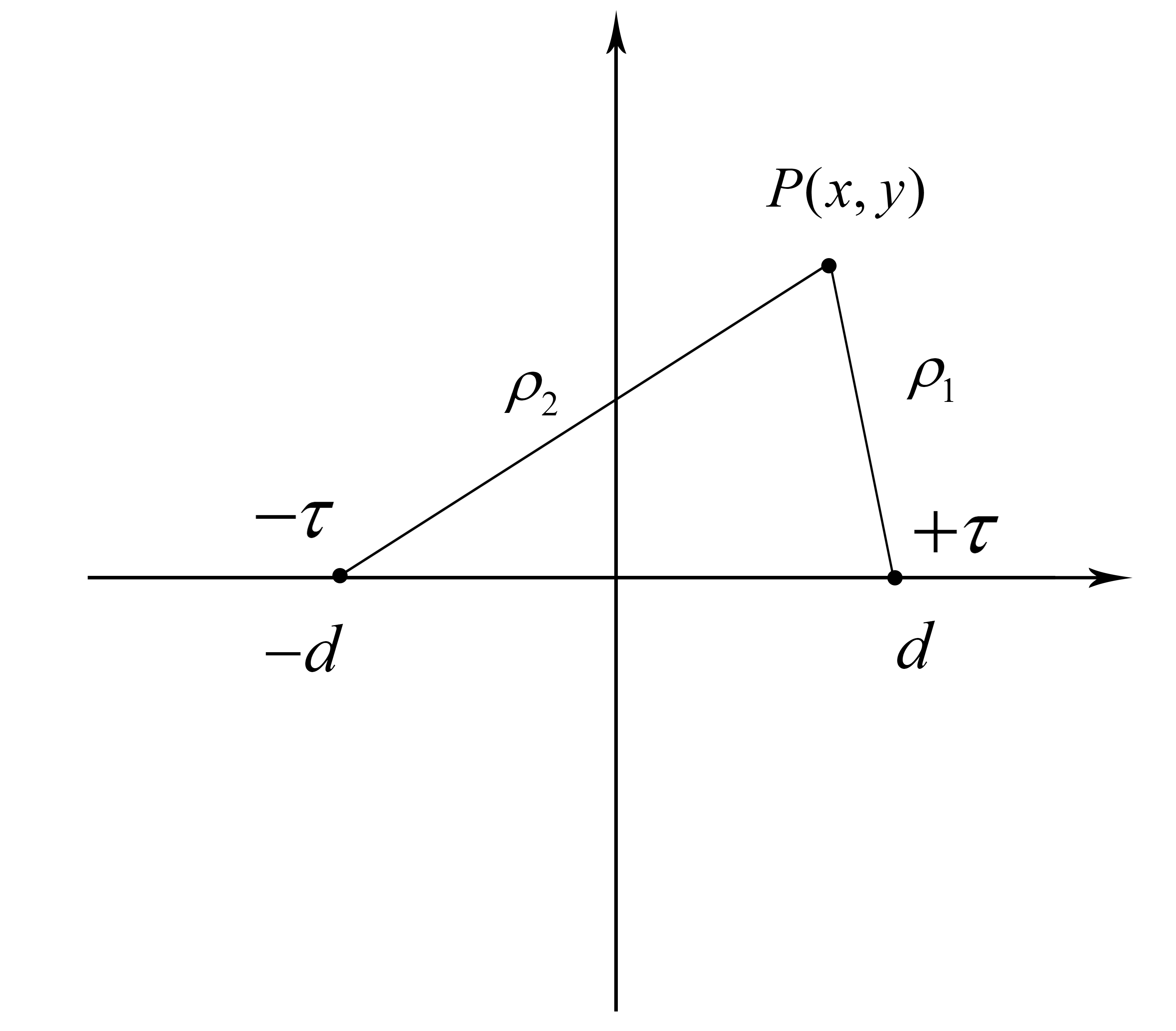
由图所示，位于P(x,y)处电场，由位于(d,0)、(-d,0)处线电荷产生的电场叠加而成：
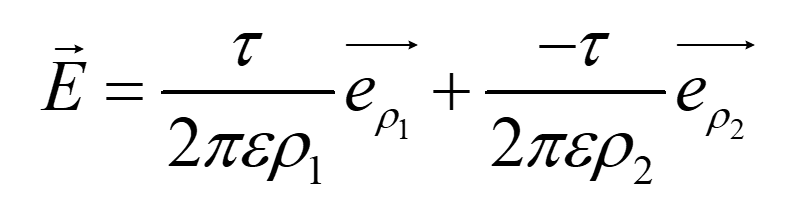
那么P点电位为：
（因为线电荷无限长，无限远处有电场，所以电位不能取0，即要加上常数C）
当将参考点取在Y轴上时，Y轴电位为0，又因为ρ1=ρ2，即可得到C=0
那么电位可写为：
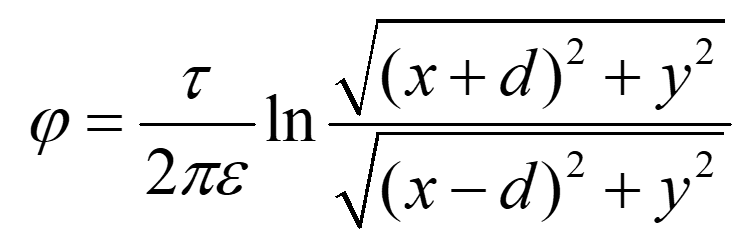
令
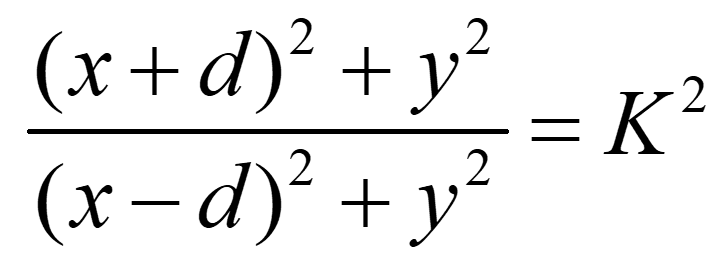
那么，当K为常数时，电位为常数，即为等位面，整理得
可以发现等位面是一系列得圆（阿波罗尼圆）
圆心(b,0)及半径R满足
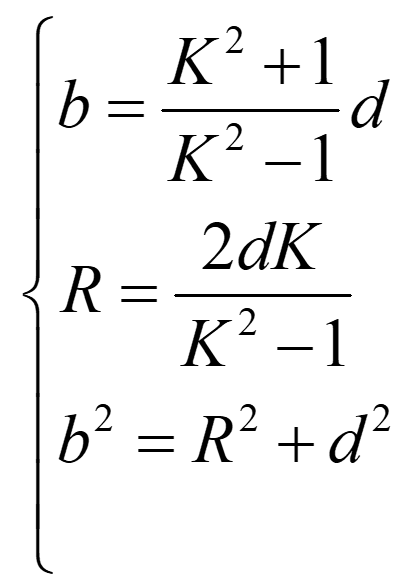
将x=b这个位置称为电轴。其意义是什么？往下看
2.两个等截面导体圆柱系统
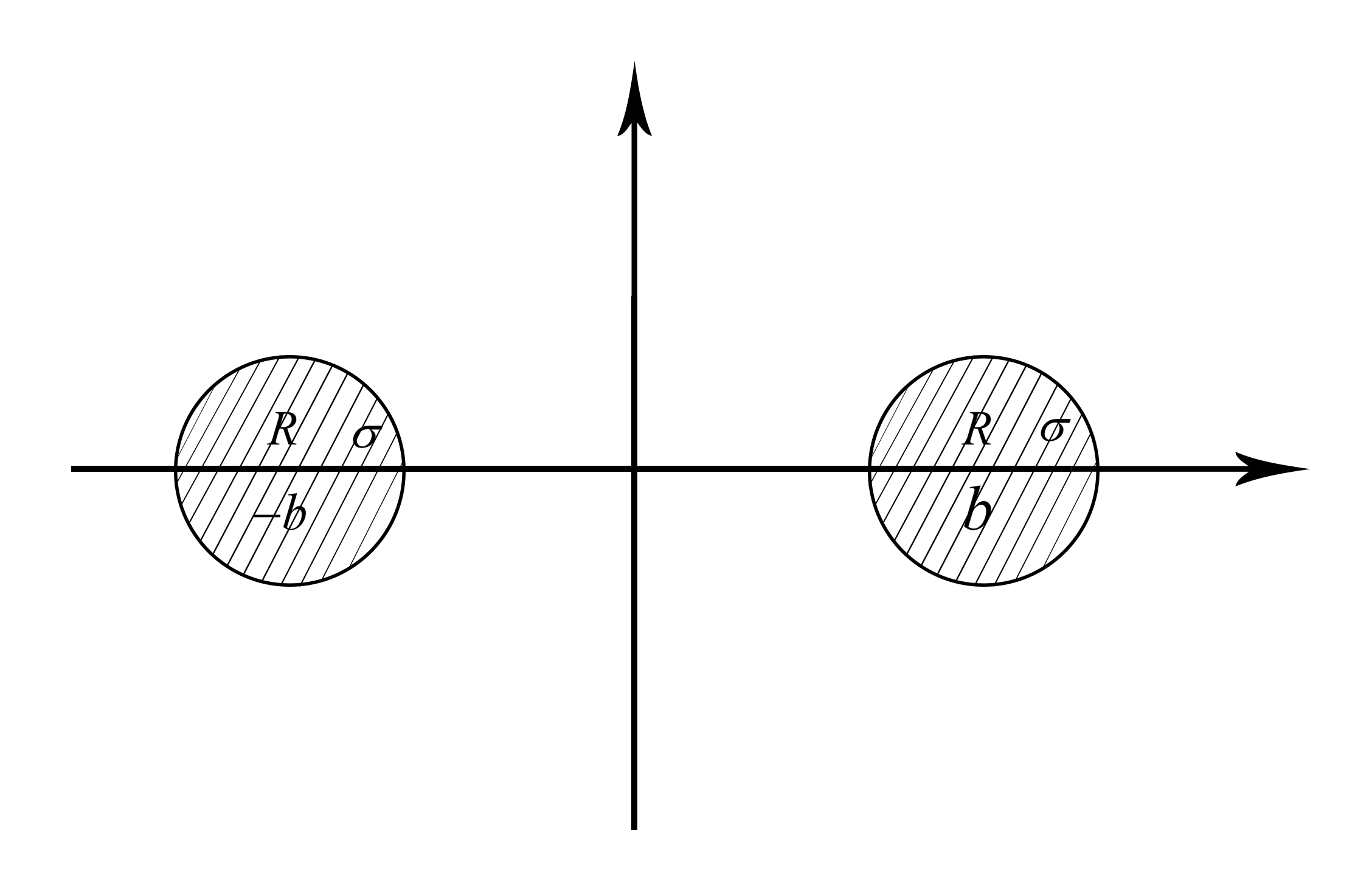
下面研究两个等截面导体圆柱系统。两个带电导体圆柱半径为R，中心轴线分别位于(b,0)、(-b,0)。由于静电场作用，两导体表面的面电荷密度必定是不均匀分布的，因而直接求解导体柱外的场是困难的。
但是，导体表面是等位面，导体每个截面的场的分布是一致的，所以可以用一个较简单的系统来与原系统等效。
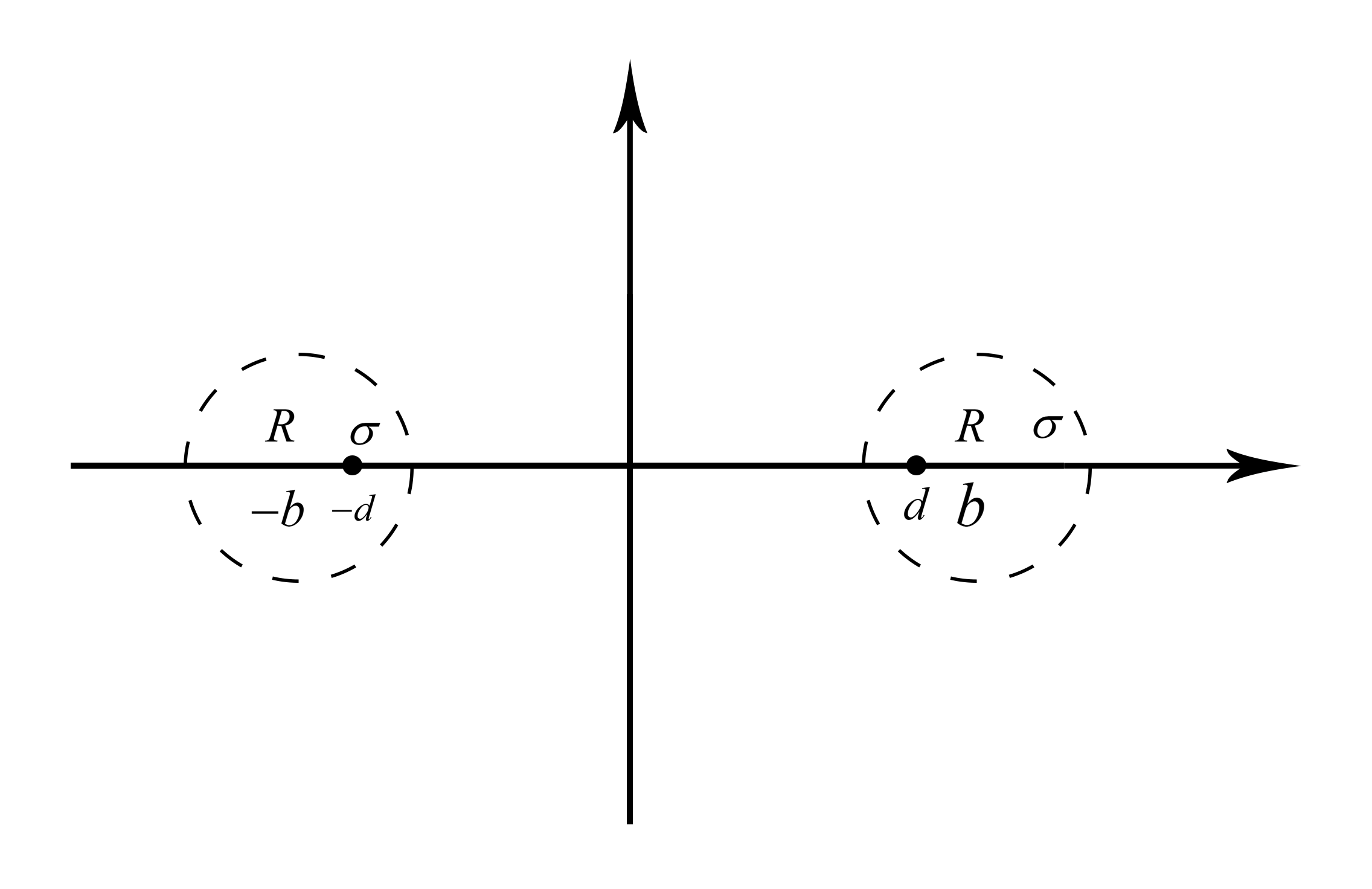
有上文可知，可以用两根位于(d,0)、(-d,0)的线电荷来等效。其中，线电荷的位置为
单位长度线电荷所带电荷量与单位长度导体圆柱所带电荷量一致。
根据唯一性定理，两系统在圆柱外的空间区域是等效的，所以求解导体圆柱外的电位分布，就转化为了求解线电荷的电位分布，这个方法就叫电轴法。
那么电位分布就是
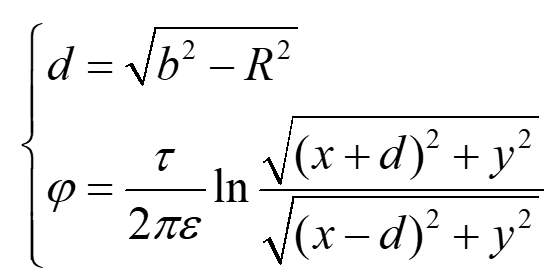
如果能测得a、b两点之间的电压U0
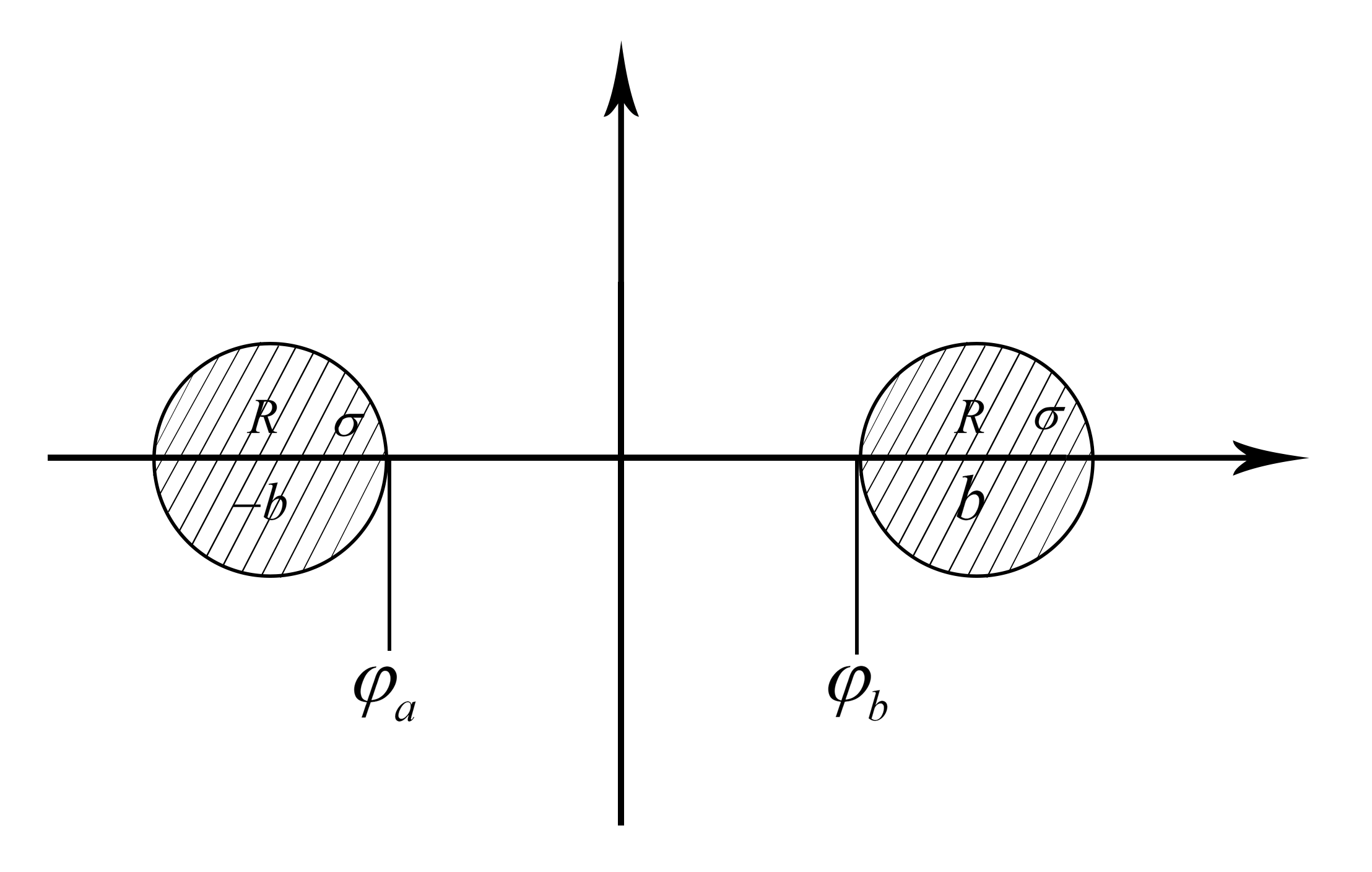
那么
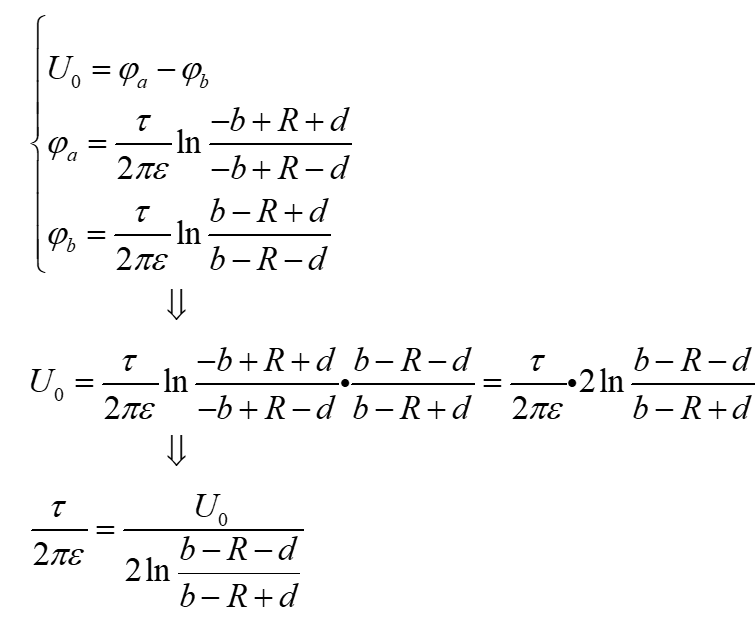
3.两截面不相等的导体圆柱系统
对于下图所示的系统，亦可用电轴法求解
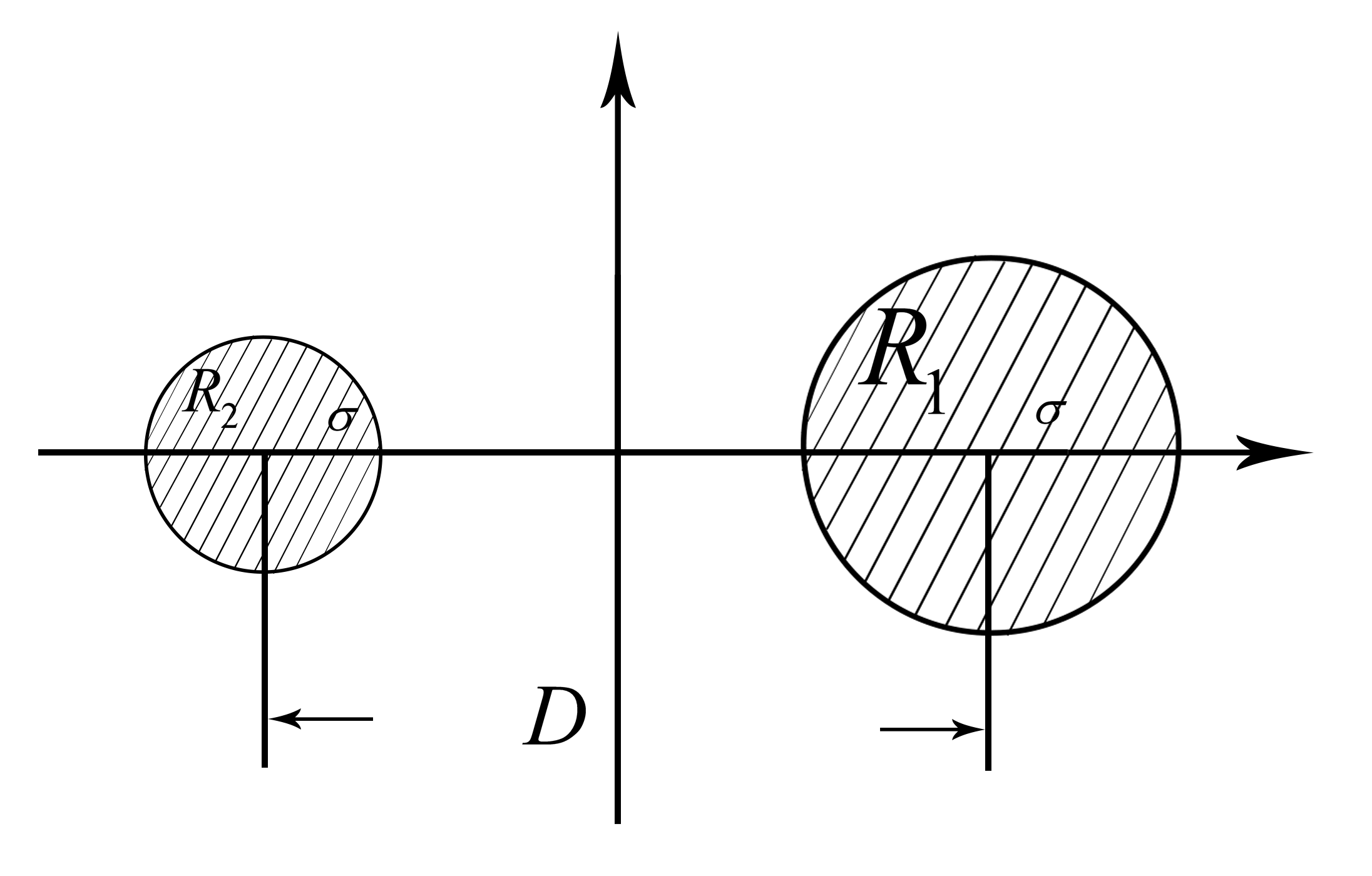
将导体圆柱等效为线电荷
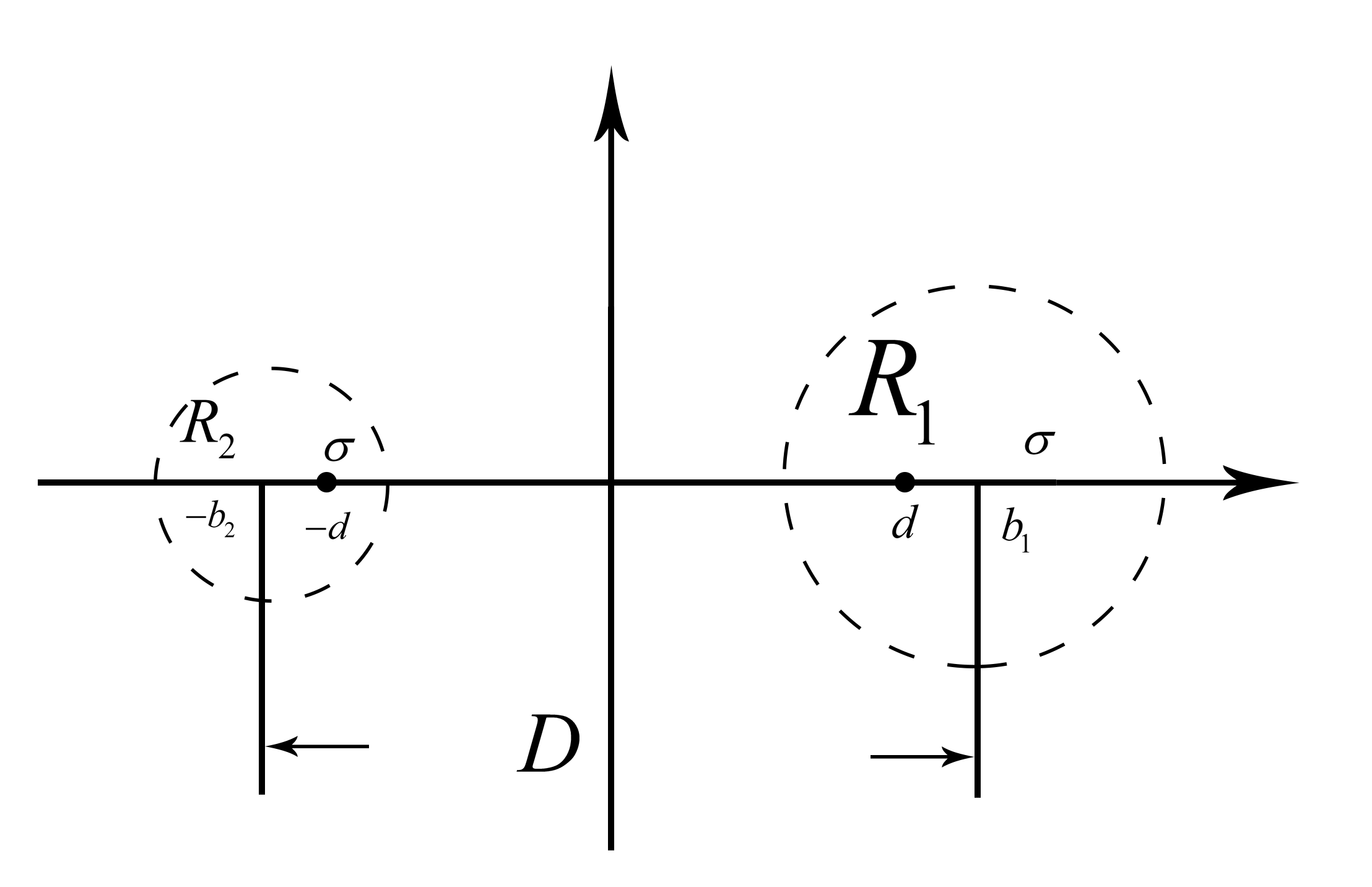
那么b1+b2=D,且
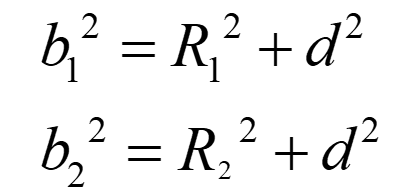
可计算出
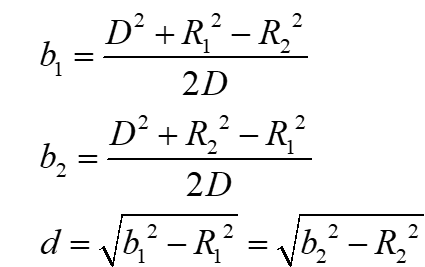
即为电轴参数，两线电荷距离为d，单位长度线电荷所带电荷量与单位长度导体圆柱所带电荷量一致。
电轴法主要应用在供电线路的线间场的计算上