目录
稀疏矩阵
●定义
• 一个阶数较大的矩阵中的非零元素个数s相对于矩阵元素的总个数t很小时,即s<<t时,
称该矩阵为稀疏矩阵
● 例:
•一个100*100的矩阵,其中只有100个非零元素
●压缩策略:
• 只存储非零元素,然后存放在表里
● 约束:
• 稀疏矩阵中非零元素的分布没有任何规律,只是顺序遍历矩阵,然后存储
● 方案:
•存储非零元素
• 同时存储该非零元素所对应的行下标和列下标
• 稀疏矩阵中的每一个非零元素由一个三元组(i,j,aij)唯一确定,稀疏矩阵中的
所有非零元素构成三元组线性表
• 说白了,就是矩阵里面元素太少,然后为了压缩存储空间,然后把矩阵里面的元素存放在 表里了
• 查找的时候,遍历表即可
● 定义存储结构
//定义一个表的最大长度,视情况而定
#define MaxSize 100//定义每个节点的数据结构
typedef struct { int r; //行号 int c; //列号 ElemType d; //元素值 }TupNode; //三元组定义//定义存储节点的表的数据结构
typedef struct { int rows; //行数值 int cols; //列数值 int nums; //非零元素个数 TupNode data[MaxSize]; //存储节点的数组 }TSMatrix; //三元组顺序表的定义
● 约定 :data 域中表示的非零元素通常以行序为主序顺序排列----下标按行有序的存储结构
● 目标 : 简化运算,按顺序的话,容易找到元素的位置,方便插入和删除,寻找
从二维矩阵创建其三元组表示
● 算法: 以行序方式扫描二维矩阵 A,将其非零元素加入到三元组t
// 传入矩阵,传入三元组顺序表 void CreateMat(TSMatrix &t, ElemType A[M][N]) { //接下来就是按顺序赋值罢了 int i,j; t.rows = M; t.cols = N; //先定义成0,然后遍历到非零元素的话,数值加一 t.nums = 0; //开始按行遍历 for(i = 0;i<M;i++) { for(j = 0; j<N;j++) { if(A[i][j] != 0) //只存储非零值 { t.data[t.nums].r = i; t.data[t.nums].c = j; t.data[t.nums].d = A[i][j]; t.nums++; } } } }
将指定位置的元素赋值给变量: 执行 x = A[i][j]
//把矩阵执行位置的元素传出,指定的位置合法的话,如果不在表里,就是0,在表里,我们就开始遍历传出即可
//传入表,存储传出元素的x,坐标 bool Assign(TSMatrix t,ElemType &x,int i,int j) { int k = 0; //验证坐标合法性 if(i>=t.rows || j>=t.cols) { return false; //失败返回false } //合法则开启遍历模式 //先遍历行,表数组位序增加,然后对比行,接着对比列即可 while(k<t.nums && i>t.data[k].r) { k++; //查找行 } //如果我们找到行,接着找列 //分开寻找,可以减少对比同一行的列 while(k<t.nums && i == t.data[k].r && j>t.data[k].c) { k++; } //跳出时,如果符合,则返回值即可 if(t.data[k].r == i && t.data[k].c == j) { x = t.data[k].d; //传入对应的值 } else { x = 0; //没找到,说明是零元素 } return true; }
三元组元素赋值 : 执行A[i][j] = x 运算
所谓赋值, 就是给矩阵里面的元素赋值,如果是对非零元素赋值,我们就修改列表里面的元素,如果是0元素赋值,我们就需要把
零元素修改,然后加入列表
● 三元素元素赋值算法
//传入列表,要赋值的值,要赋值的坐标 bool Value(TSMatrix &t,ElemType x,int i,int j) { int k = 0,k1; //判断输入的合法性 if(i>=t.rows || j>=t.cols) { return false; //失败时返回false } while(k<t.nums && i>t.data[k].r) { k++; //查找行 } while(k<t.nums && i==t.data[k].r &&j >t.data[k].c) { k++; //查找列 } if(t.data[k].r == i && t.data[k].c==j) { t.data[k].d=x; } else{ // 不存在时要插入 //同时完成移动操作 //即完成顺序表的插入操作 for(k1=t.nums-1;k1>k;k1--) { t.data[k1+1].r=t.data[k1].r; t.data[k1+1].c=t.data[k1].c; t.data[k1+1].d=t.data[k1].d; } t.data[k].r=i; t.data[k].c=j; t.data[k].d=x; t.nums++; }//不存在时要插 return true;//成功时返回true }
输出三元组
● 从头到尾扫描三元组t,依次输出元素值
//传入列表 void DispMat(TSMatrix t) { int i; if(t.numsl<= 0) { return; } printf("\t%d\t%d\t%d\n",t.rows,t.cols,t.nums); printf("--------------\n"); //遍历输出 for(i=0;i<t.nums;i++) { printf("\t%d\t%d\t%d\n",t.data[i].r,t.data[i].c,t.data[i].d); } } 矩阵转置 ● 对于一个m * n 的矩阵A m*n,其转置矩阵是一个n * m的矩阵 B n*m,满足 bij = bji,其中 (0<= i <=m-1,0<= j <= n-1) void TranTat(TSMatrix t,TSMatrix &tb) { int p = 0; int q = 0; int v; tb.rows = t.cols; tb.cols = t.rows; tb.nums = t.nums; if(t.nums != 0) //当存在非零元素时 { //先遍历t的列,因为我们要对转置的行进行部署 for(v=0; v<t.tols; v++) { for(p=0; p<t.nums; p++) { if(t.data[p].c == v) { tb.data[q].r = t.data[p].c; tb.data[q].c = t.data[p].r; tb.data[q].d = t.data[p].d; q++; } } } } }
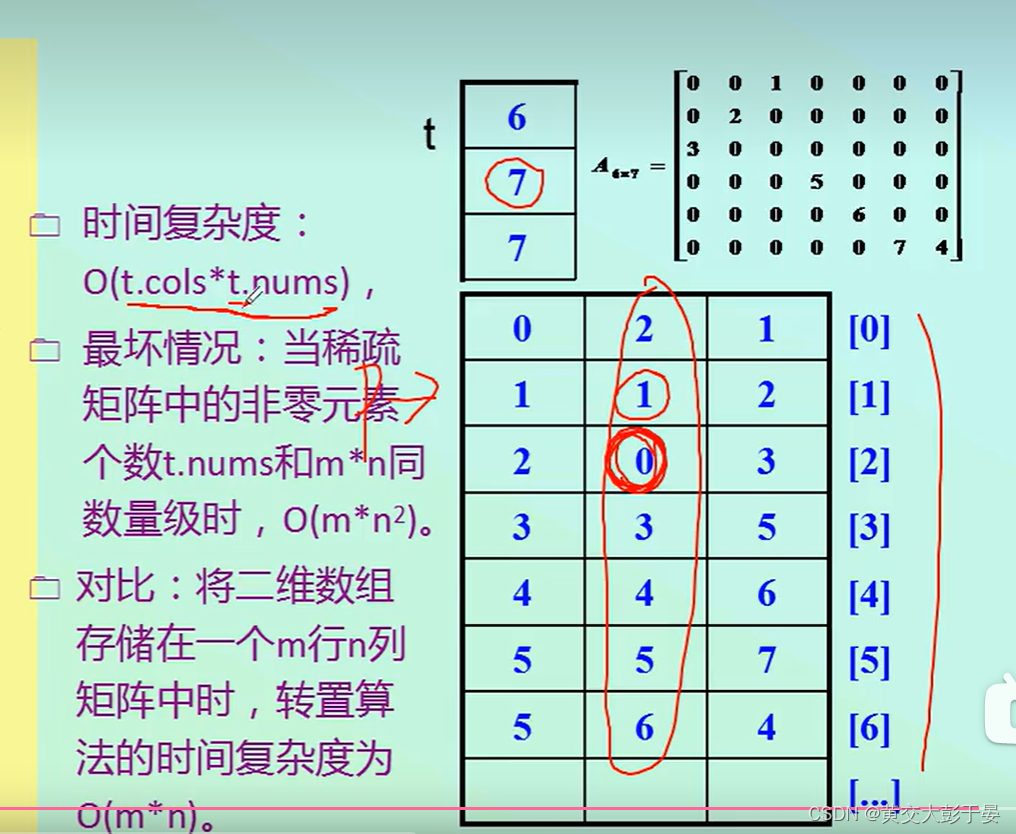
复杂度分析:
占用时间复杂度过大, 我们要衡量空间和时间之间的关系, 这是一个永恒的话题,我们一般采用折中的算法.