🎇C++笔试强训
- 博客主页:一起去看日落吗
- 分享博主的C++刷题日常,大家一起学习
博主的能力有限,出现错误希望大家不吝赐教- 分享给大家一句我很喜欢的话:夜色难免微凉,前方必有曙光 🌞。
💦🔥
选择题
💦第一题
二分查找的时间复杂度()
A O(N*log(N))
B O(N)
C O(log(N))
D O(N^2)
二分查找的数据要求是有序的,根据前后两个下标得出中间节点,然后拿key和他相比,如果大则在右区间继续找,小则左区间,每次比较会少一半数据,依次重复使用这种方法
得出公式 2 ^ x = n ——》 x = log2(n)
这道题的答案是C
💦第二题
有一个单向链表中有一个A、B两个相邻元素,有一个指针p指向元素A,现将一个指针r指向的S元素要插入到A和B之间,该进行操作()
A p->next=p->next->next
B r-next=p;p->next=r->next
C r->next=p->next;p->next=r
D r=p->next;->next=r->next
E r->next=p;p->next=r
F p=p->next->next
这道题考察单链表的插入,数据结构的题需要多画图
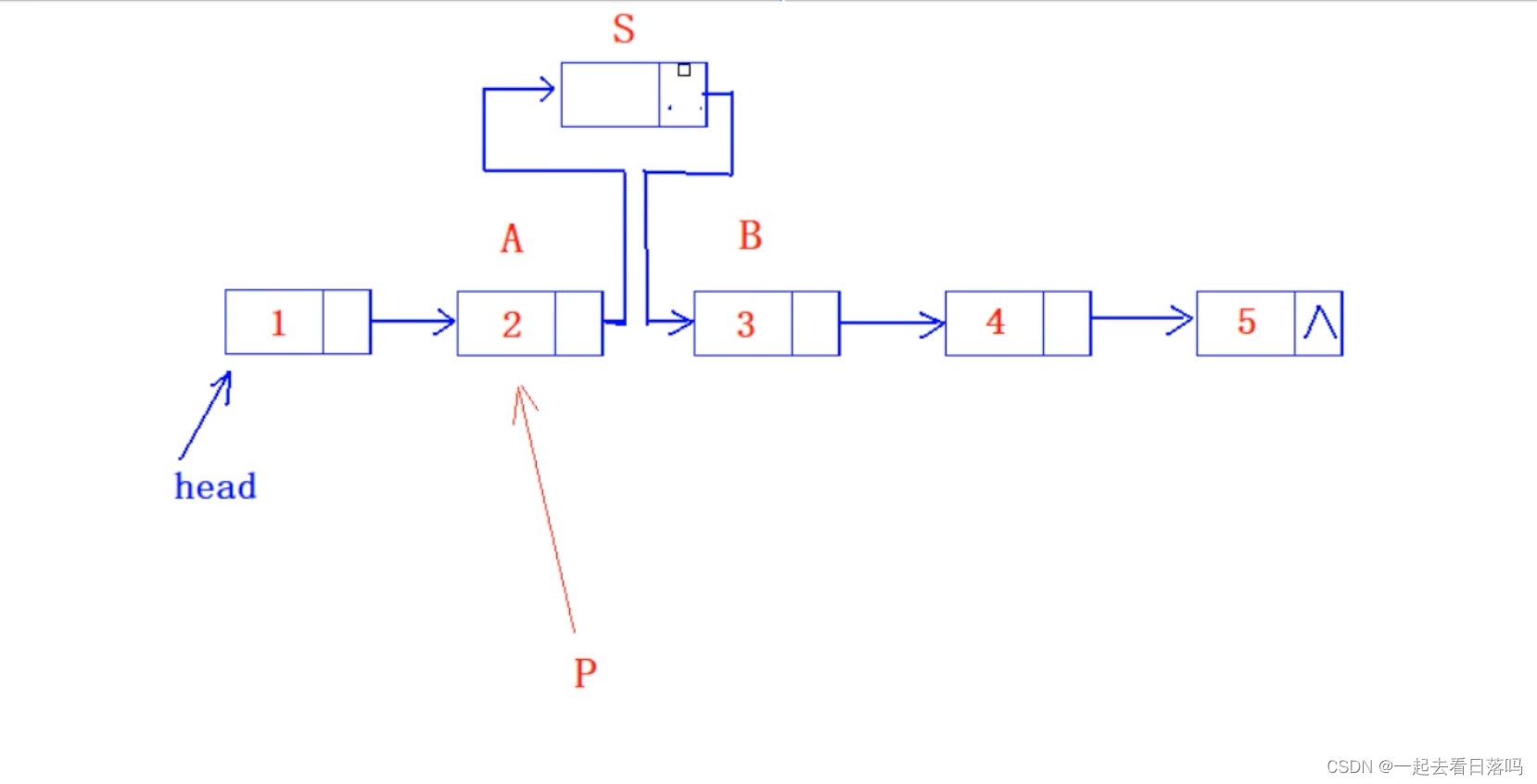
这道题的答案是C
💦第三题
双向链表中有两个指针域,llink和rlink分别指向前驱和后继,设p指向链表中的一个结点,现要求删去p所指结点,则正确的删除是()(链中结点数大于2,p不是第一个结点)
A p->llink->rlink:=p->llink; p->llink->rlink:=p->rlink; dispose§;
B dispose§; p->llink->rlink:=p->llink; p->llink->rlink:=p->rlink;
C p->link->rlink:=p->llink; dispose§; p->llink->rlink:=p->rlink;
D 以上A,B,C都不对
已知不是删除头节点
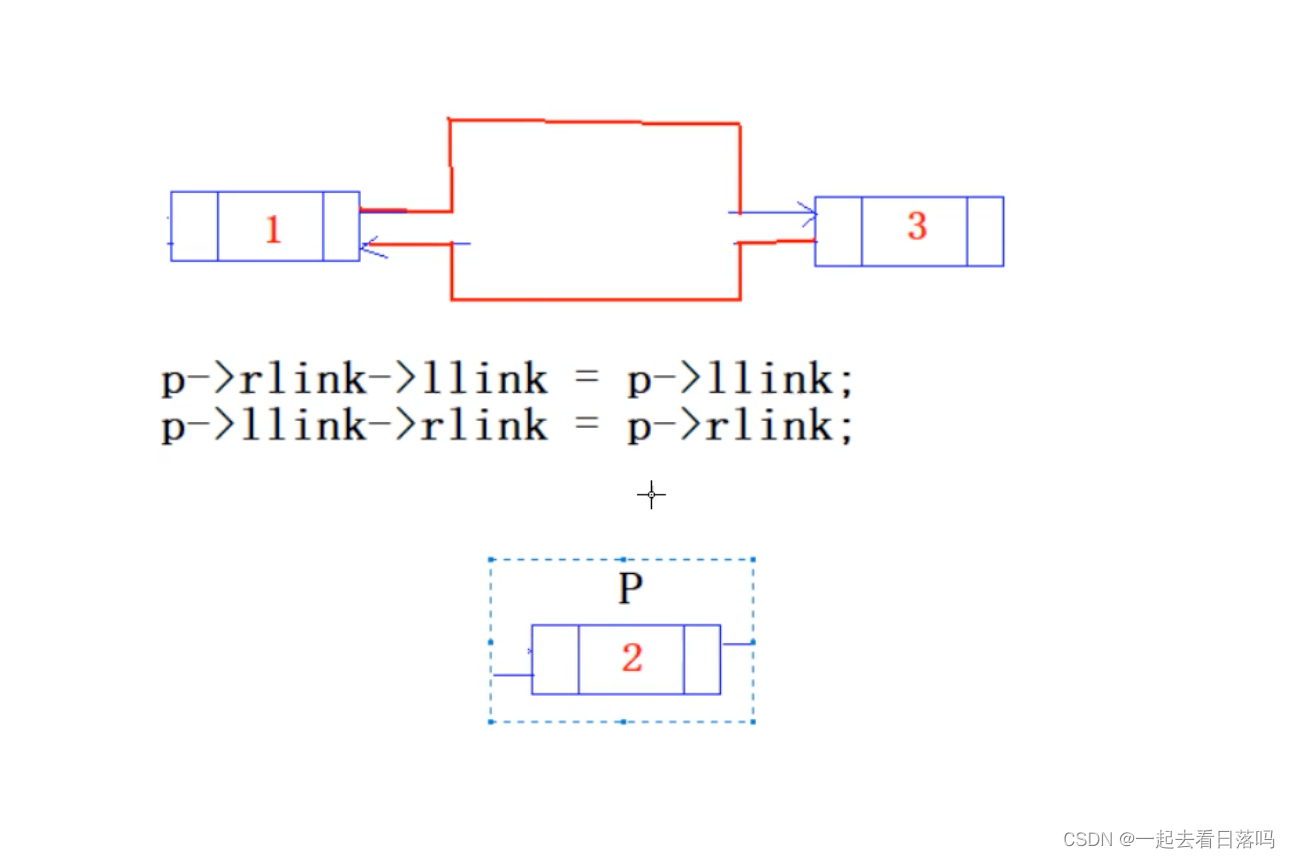
如果要释放节点就会delete p;
这道题的答案是D
💦第四题
一个栈的入栈序列是A,B,C,D,E,则栈的不可能输出序列是()
A EDCBA
B DECBA
C DCEAB
D ABCDE
这是考察栈的性质,栈是后入先出,这种题基本都是送分题
这道题的答案是C
💦第五题
循环队列放在一维数组A[0…M-1]中,end1指向队头元素,end2指向队尾元素的后一个位置。假设队列两端
均可进行入队和出队操作,队列中最多能容纳M-1个元素。初始时为空,下列判断队空和队满的条件中,正
确的是()
A 队空:end1 = = end2;队满:end1 = =(end2+1) mod M
B 队空:end1= =end2;队满:end2==(end1+1) mod (M-1)
C 队空:end2==(end1+1) mod M;队满:end1==(end2+1) mod M
D 队空:end1==(end2+1) mod M;队满:end2==(end1+1) mod (M-1)
数据结构的题目需要多画图,只要有图所有的问题都会迎刃而解
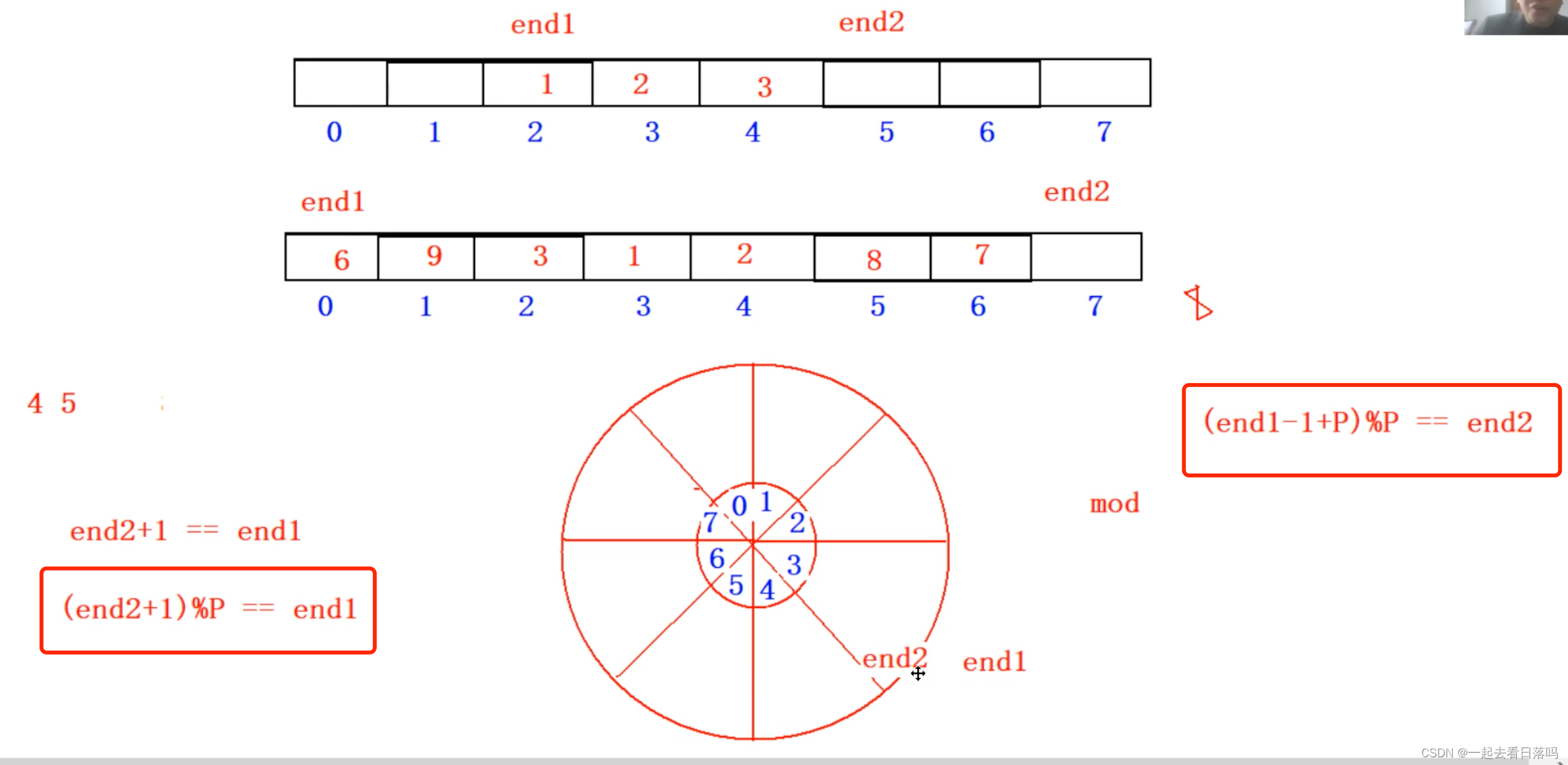
这道题的答案是A
💦第六题
已知二叉树后序遍历序列是bfegcda,中序遍历序列是badefcg,它的前序遍历序列是()
A abcdefg
B abdcefg
C adbcfeg
D abecdfg
二叉树必须有中序和其他排序才可以确定二叉树,只需要知道排序方法是怎么样就可以恢复出来了
中序确定左右
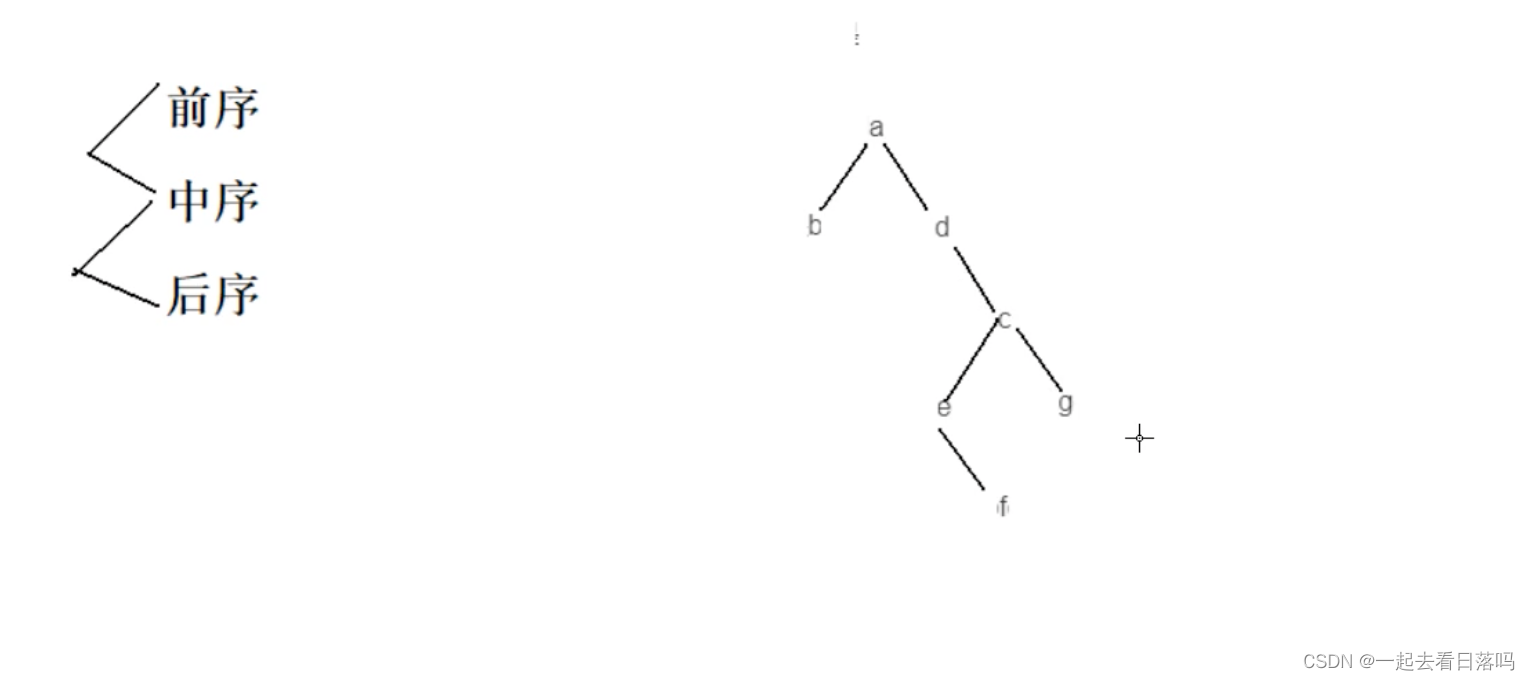
这道题的答案是B
💦第七题
某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为()
A 不存在这样的二叉树
B 200
C 198
D 199
这道题如果知道二叉树的性质,做道题很简单

这道题的答案是B
💦第八题
以下序列不是堆的是()
A (100,85,98,77,80,60,82,40,20,10,66)
B (100,98,85,82,80,77,66,60,40,20,10)
C (10,20,40,60,66,77,80,82,85,98,100)
D (100,85,40,77,80,60,66,98,82,10,20)
A选项是个大堆
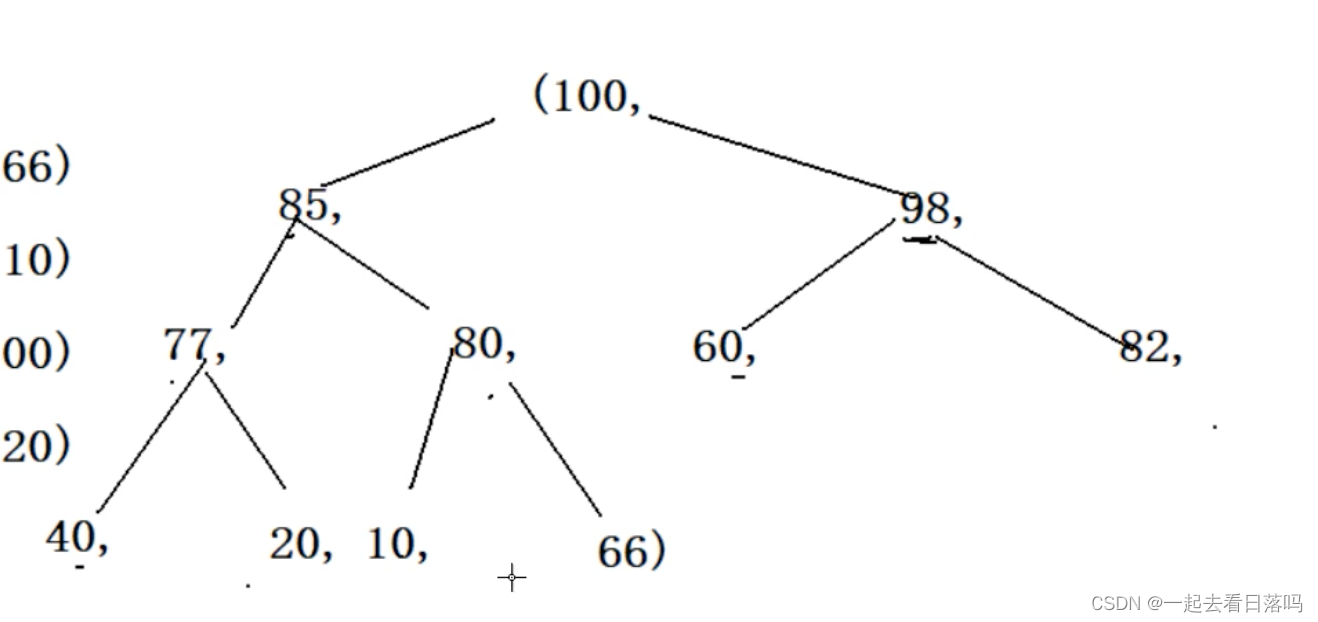
B选项也是个大堆
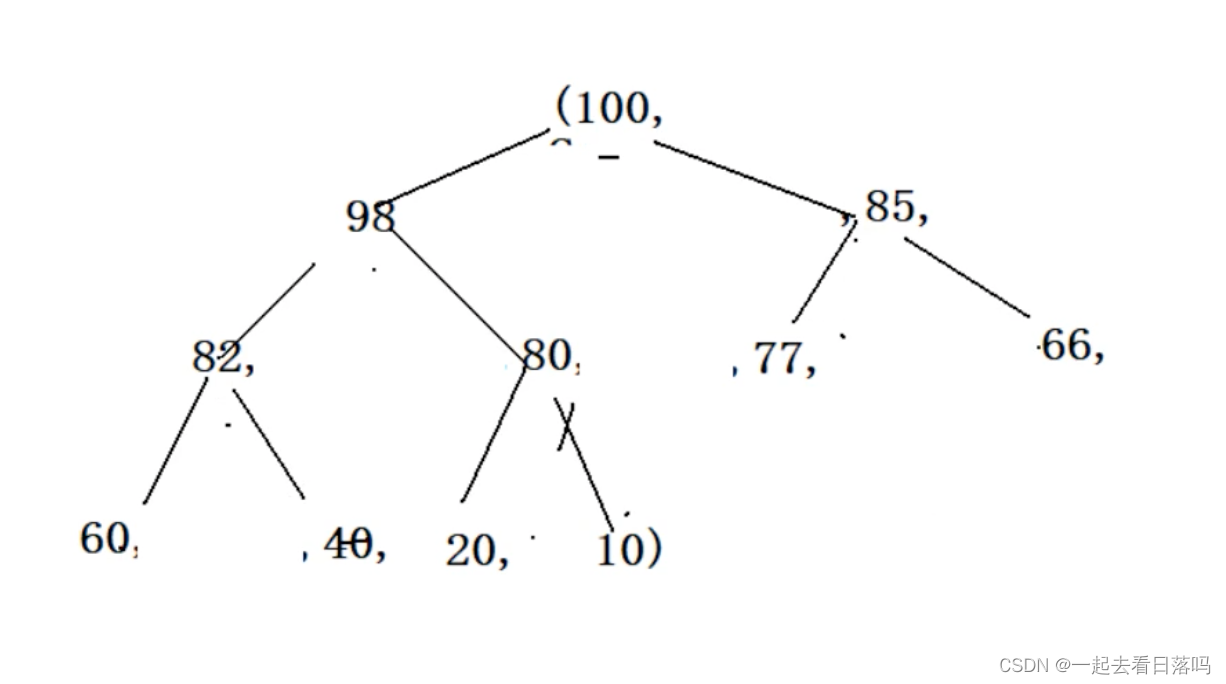
C选项是个小堆
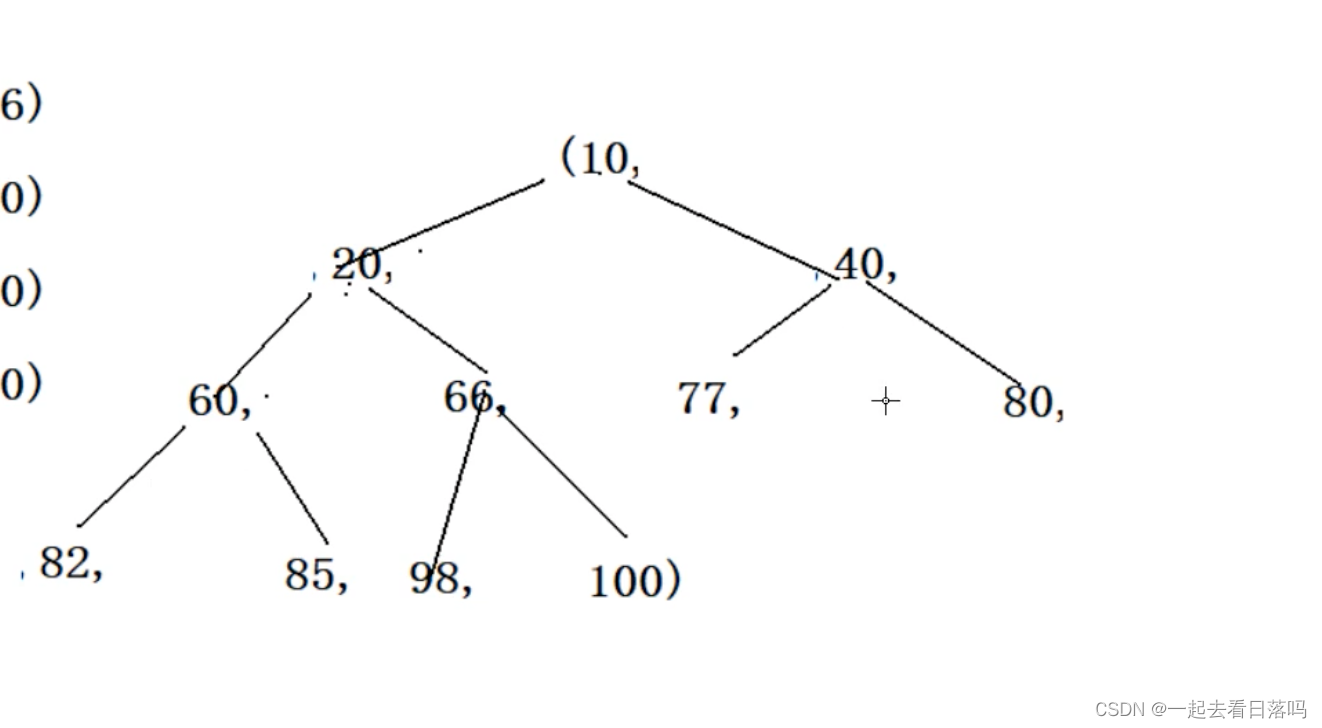
D不是堆
这道题的答案是D
💦第九题
设有一组记录的关键字为{19,14,23,1,68,20,84,27,55,11,10,79},用链地址法构造哈希表,哈希函数为H(key)=key MOD 13,哈希地址为1的链中有()个记录
A 1
B 2
C 3
D 4
只要将数据%13 得的值是1 的数据统计起来就可以知道了
这道题的答案是D
💦第十题
以下哪种排序是不稳定排序()
A 冒泡
B 插入排序
C 归并排序
D 快速排序
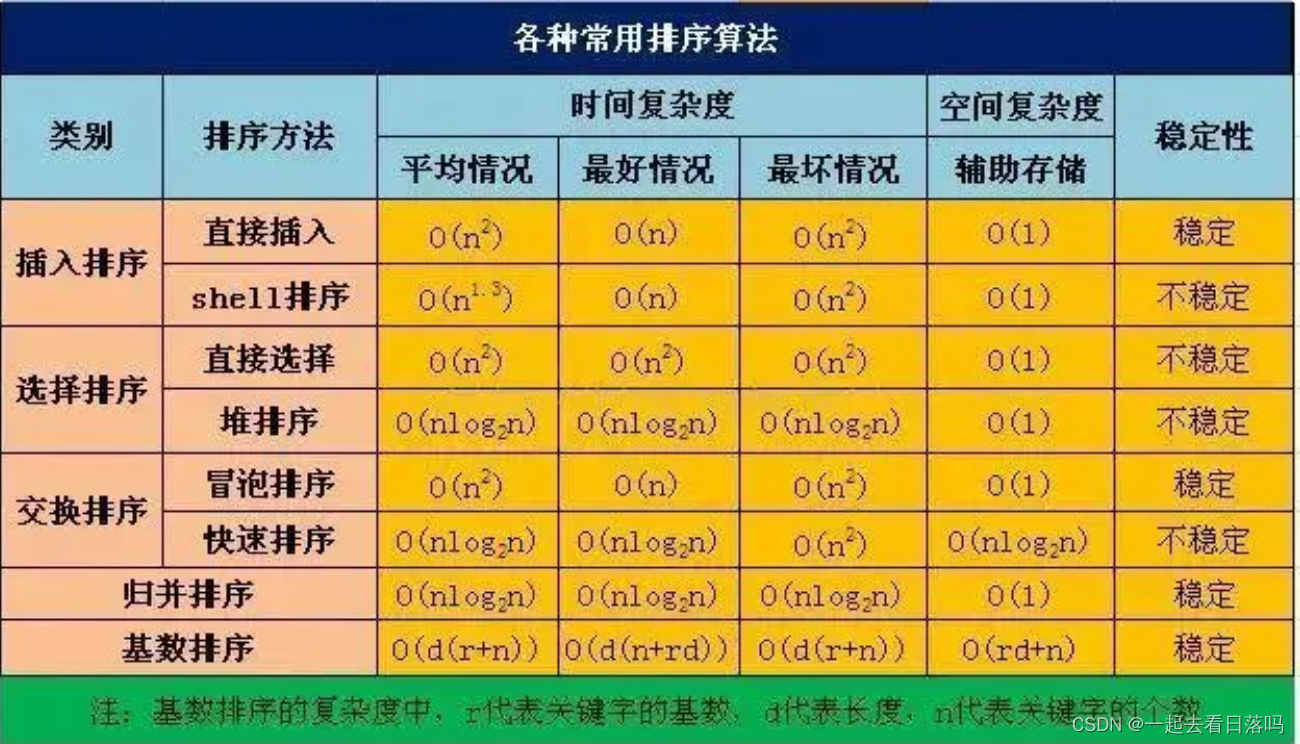
越快的越不稳定,现实里淹死的都是会游泳的
这道题的答案是D``
编程题
🔥 第一题
链接:汽水瓶

- 解题思路
本题题意简单,每次空瓶的数量除以2,直到最后空瓶的数量少于两瓶,就累加到了课兑换的数量。
- 代码演示
#include <iostream>
using namespace std;
//方法一:概念法
int calcNumber_1(int n)
{
int sum = 0;
while(n > 1)
{
int res = n / 3; //所能兑换的个数
int left = n % 3; //遗留个数
sum += res;
n = left + res;
if(n == 2)
{
sum++;
break;
}
}
return sum;
}
//方法二:取巧法
int calcNumber_2(int n)
{
return n/2;//观察结果,能喝的数目是空瓶子的一半
}
int main()
{
int n,res;
while(cin >> n)
{
if(n == 0)
break;
//res = calcNumber_1(n);
res = calcNumber_2(n);
cout << res << endl;
}
return 0;
}
🔥 第二题
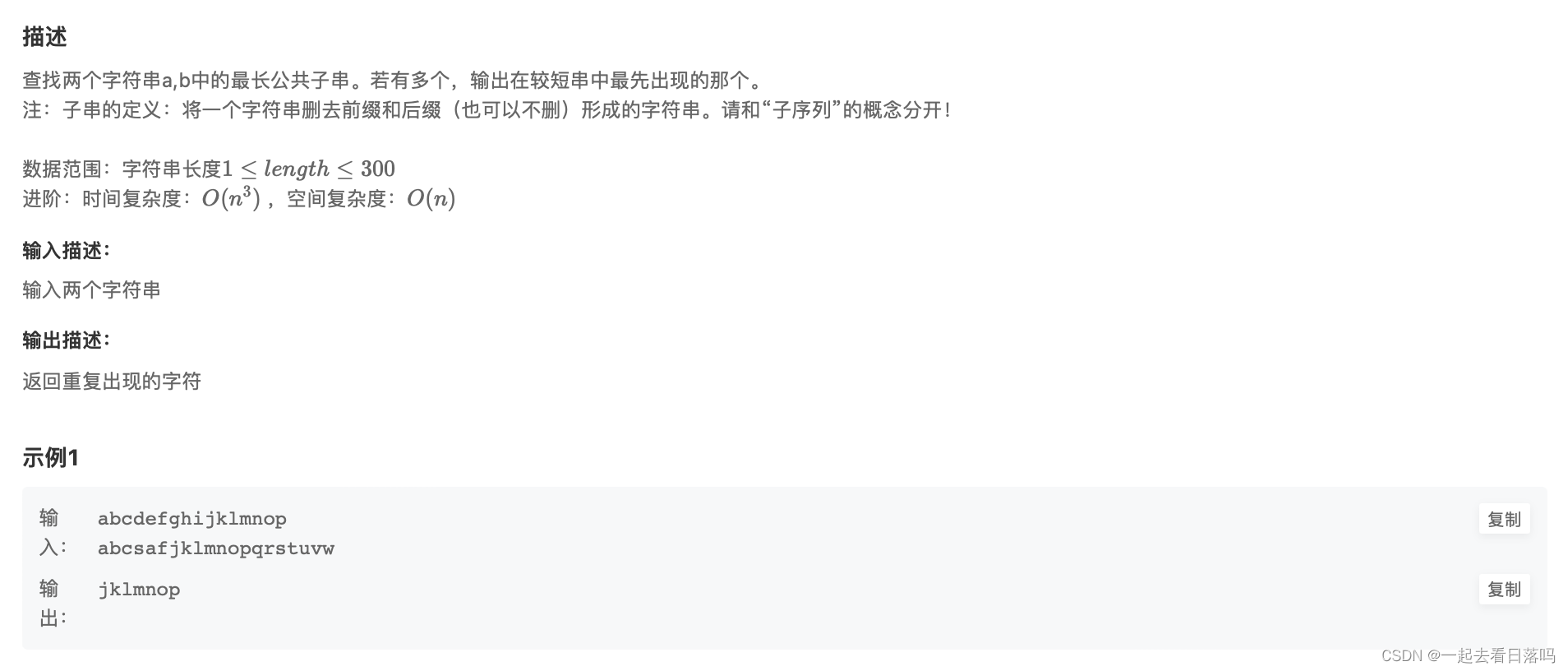
- 解题思路
本题需要用动态规划求解,MCS[i][j]记录短字符串 s1 前 i 个字符和长字符串 s2 前 j 个字符的最长子串的长度,初始化所有值为 0。当 s1[i-1] = s2[j-1]时,MCS[i][j] = MCS[i - 1][j - 1] + 1,这里使用一个额外的值start 来记录最长子串在短字符串 s1 中出现的起始位置,maxlen记录当前最长子串的长度,当MCS[i][j] >maxlen 时,maxlen = MCS[i][j], 则start = i - maxlen ;档s1[i-1] != s2[j-1]时不需要任何操作,最后获取substr(start, maxlen)即为所求。
- 代码演示:
#include <iostream>
#include <string>
#include <vector>
using namespace std;
string getComSubstr(string &str1,string &str2)
{
if(str1.size() > str2.size())
swap(str1,str2);
int len1 = str1.size();
int len2 = str2.size();
int start = 0,max_size = 0;
vector<vector<int>> MSC(len1+1 ,vector<int>(len2+1 , 0));
for(int i = 1;i < len1;++i)
{
for(int j = 1;j < len2;++j)
{
if(str2[j - 1] == str1[i - 1])
MSC[i][j] = MSC[i - 1][j - 1] + 1;
if(MSC[i][j] > max_size)
{
max_size = MSC[i][j];
start = i - max_size;
}
}
}
return str1.substr(start,max_size);
}
int main()
{
string str1,str2;
while(cin >> str1 >> str2)
{
string substr = getComSubstr(str1,str2);
cout << substr << endl;
}
return 0;
}
