0. 前言

Hello，大家好，我是anduin。这期的内容依然是链表OJ。但与前两期不同的是，这次我会模拟面试的情景，由浅入深，以生动形象的方式，带你一步步吃透这些OJ题。内容为 经典的环形链表系列问题、复制带随机指针的链表这一十分考验链表功底的题目 。总体来说，题目还是有一定难度的，所以，接下来打起精神，认真看完，相信你会收获很多！话不多说，我们这就开始！

注：本故事纯属虚构，仅为配合题目的讲解，如有雷同实属巧合。

1. 环形链表

众所周知，单链表是面试的常考点，假设你明天准备二面。由于时间不够了，你的链表基础也还行，所以你打算背两道题目，万一就考到了呢？于是你在链表题集中翻到了这道题。

链接：141. 环形链表

描述：

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。**注意：pos 不作为参数进行传递 。仅仅 是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

示例1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例2:：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

提示：

• 链表中节点的数目范围是 [0, 10^4]
• -10^5 <= Node.val <= 105
• pos 为 -1 或者链表中的一个 有效索引 。

你一看题目，懵逼了。这带环链表可咋做啊！于是你翻开了力扣的答案册，看到了某个帅哥(假设是我)的题解。于是你打算看看。

思路(精讲)：

做这道题目之前我们需要明确一点 不能遍历链表 ，因为链表带环。

链表带环就是链表的某个节点中存储的地址为这个节点前的某个节点的地址。而导致闭环 ，使遍历链表时无法停止，走不到空，无法停止。

所以我们这道题目采用的方法是 快慢指针 。

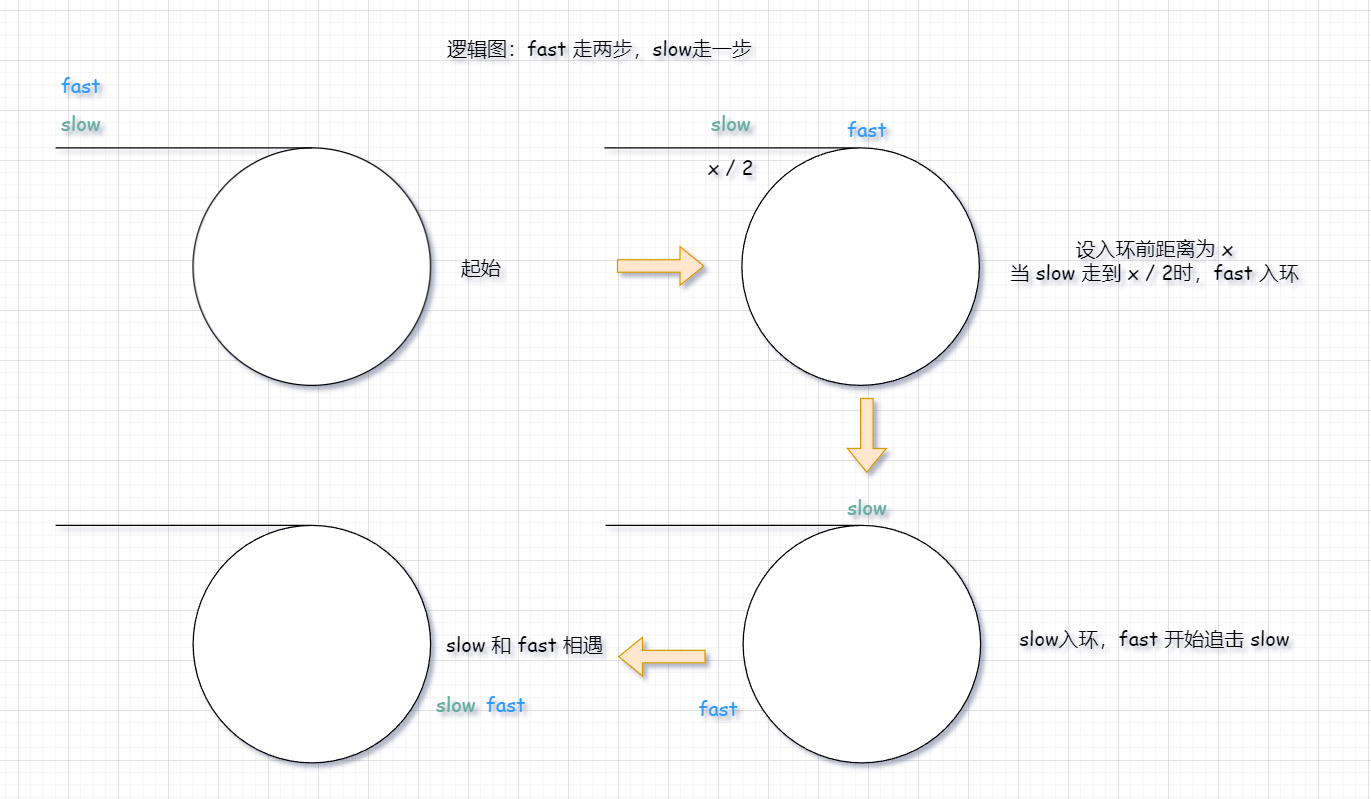
总体思路是这样的，快指针走两步，慢指针走一步。给定快指针 fast ，慢指针 slow ，初始值为链表的头。

设入环前的距离为 x 。当 slow 走了 x/2 时，fast 入环。fast 走了一段路程后，slow 入环，fast 开始追击 slow，最后 fast 和 slow 相遇。

而这里面的走法，就和我们上篇博客中，求链表的中间节点的方法一样。奇数走到最后一个节点，偶数走到空。

如果走到这两个条件了，说明链表一定不带环。否则不会走到空，它们一定会相遇，为环形链表。

你一看思路，我去这么多！我就背个代码吧，反正到时候应该也就只考代码，我只要记住这个方法叫 快慢指针 就好了呗！
然后你背了两道题目后，准备睡觉。

2. 环形链表延伸问题

第二天，你进入了面试的房间。

你坐到面试官的对面。面试官笑嘻嘻地问你：“小伙子，环形链表 会吗”？然后笑眯眯地拿了一张纸给你，这张纸上恰好就是这道题。

你看到题目，心里十分兴奋，那不是我昨天背的题目吗！笑哈哈地说：“那可是我的拿手好戏！” 然后提笔唰唰唰地就把题目写完了。

面试官看了一眼，眉头一皱，嘴角一抿，然后恢复笑容，说：“那我考考你，你是怎么想到的呀？”

你一听，以为面试官不知道你的方法，然后自信地说：“ 快慢指针 ！”但是说完你后悔了，面试官问的是怎么想到的，这我咋会，我只会写，我说不出来呀…

面试官听到这里，好像察觉到了你内心的慌张，微微一笑，说：“那么你这么懂这个方法，那我问你几个问题吧！”

好了注意了，大家！接下来，请听题：

问题1：“为什么 slow 和 fast 指针一定会在环中相遇？会不会错过，永远追不上？请证明一下？”

听到这个问题，你内心一紧，表情略微苦涩。面试官观察到了你的表情，笑容越发嚣张，继续问：

问题2：“为什么 slow 走一步，fast 走两步？能不能 fast 一次走 n 步 (n > 2) ？请证明一下？”

你懵了，说：“我不会…。”

面试官笑着对你说：“小伙子，你还是太嫩了呀！想知道这是为啥吗？”

你十分憋屈地说：“不知道。您能讲讲吗？”

面试官歪嘴一笑：“说，想学啊？我教你啊！”

于是面试官就开始了他的表演，期间举止十分嚣张，一言一语透露着自信。

接下来不会的小伙伴听好了，面试官(也就是我，哎嘿)来为大家讲问题！

---

问题1：“为什么 slow 和 fast 指针一定会在环中相遇？会不会错过，永远追不上？请证明一下？”

第一步：slow 和 fast ，fast 一定是先进环。这时 slow 走了入环前距离的一半。

第二步：随着 slow 进环，fast 已经在环里走了一段了。走了多少跟环的大小有关。

假设 slow 进环时，slow 和 fast 的距离是 N。N 的长度一定小于环。

fast 开始追 slow ，slow 每次往前走 1 步，fast 往前走 2 步。每追一次，判断一下是否相遇。

每追 1 次，fast 和 slow 的距离变化：N -> N - 1 -> N - 2 … 1 -> 0.

每追 1 次，距离减少 1 。它们最后的距离减到 0 时，就是相遇点。

所以说，她逃他追，她插翅难飞。
额，不对，是快指针走两步一定会追到慢指针。
嗯对，接下来看下一个问题。

---

问题2：“为什么 slow 走一步，fast 走两步？能不能 fast 一次走 n 步 (n > 2) ？请证明一下？”

既然面试官这么问了，那么我们不妨走 n（n > 2） 步试一下。假设我们 slow 走一步，fast 走三步。

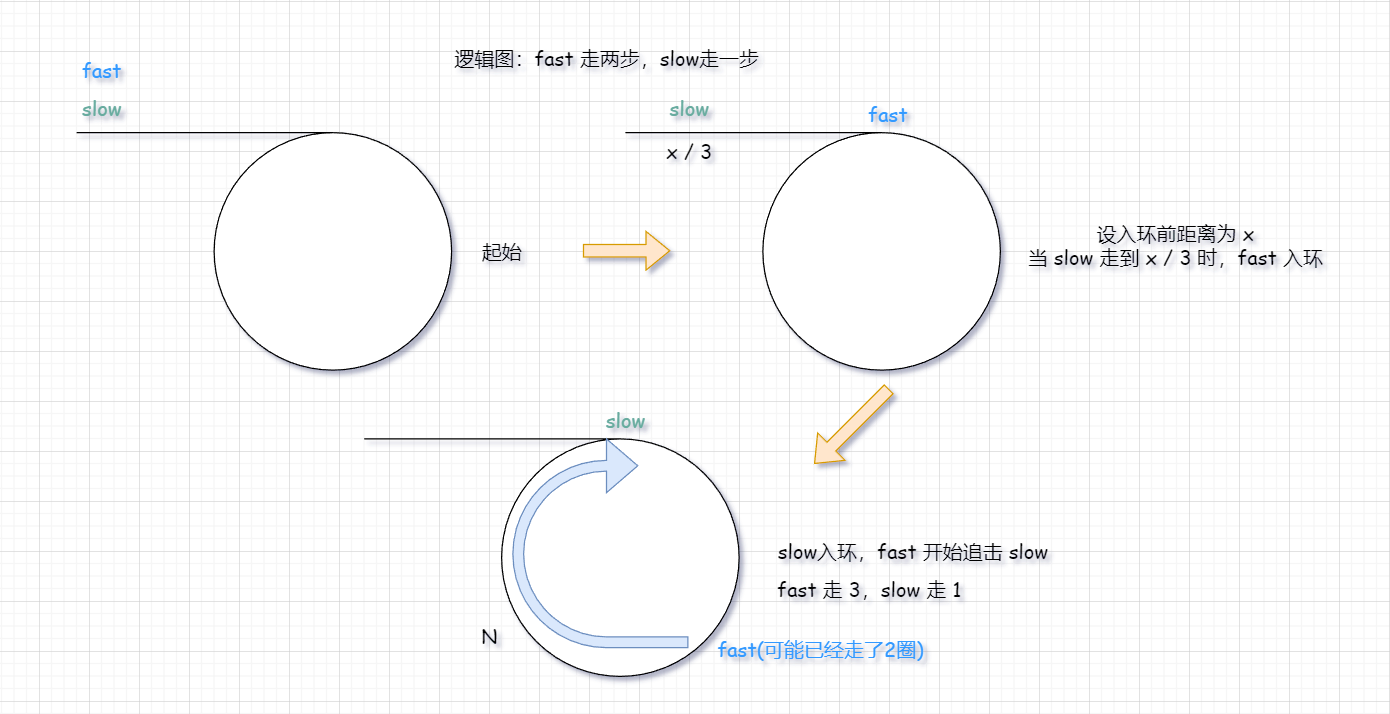
它们之间的 距离变化 如下：

N 是偶数	N 是奇数
N	N
N - 2	N - 2
N - 4	N - 4
N - 6	N - 6
…	…
2	1
0	-1
可以追上	这一次追不上

注: N 是 fast 和 slow 之间的距离。

当 N 是 奇数 时，如果 fast 走 3 步， slow 走 1 步，一个周期是肯定追不上的。走到最后它们之间的距离变为 -1 ，意味着现在 fast 在 slow 前面一步，它们之间的距离变为 c - 1 。（c 是环的长度）

而长度一旦为 c-1 就有会引申出两种情况，看下图：

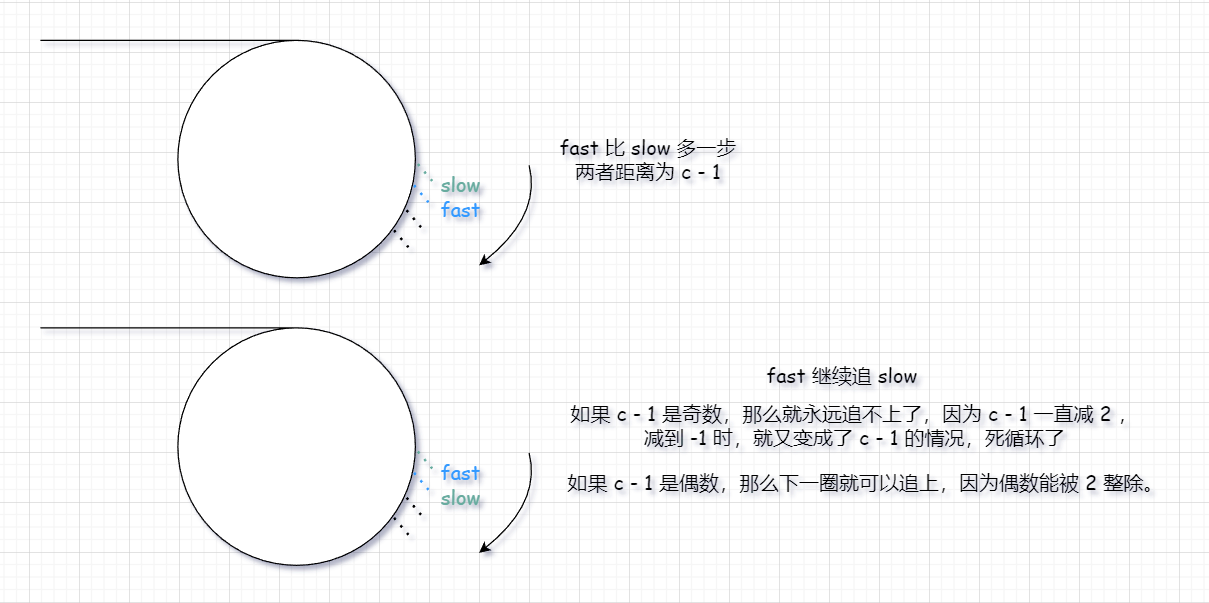
我们这里已经 初步证明 了当 fast 一次走 n(n > 2) 步时，fast 是不一定可以追上 slow 的。

举了一个 fast 走 奇数步 的例子，我们再举一个 fast 一次走 偶数步 的例子。

假设 fast 一次走 4 步，slow 一次走 1 步。

N 是 3 的倍数	N 不是 3 的倍数(N是 1 的倍数)	N 不是 3 的倍数(N 是 2 的倍数)
N	N	N
N - 3	N - 3	N - 3
N - 6	N - 6	N - 6
N - 9	N - 9	N - 9
…	…	…
3	2	1
0	-1	-2
可以追上	这一次追不上	这一次追不上

假设 c 是环的长度。

-1 意味着距离是 c - 1，-2 意味着距离是 c - 2。

如果 c - 1 和 c - 2 是 3 的倍数就可以追上，否则就追不上。

然后就可以以此类推，我就不多赘述了~

结论：fast 走 2 步，slow 一定可以追上，因为它们的距离逐次减 1 。但是当 n > 2 时，不一定会相遇。

---

随后面试官再次笑眯眯地问：“同学，你懂了吗？”

你说：“我懂了，请问帅气的面试官，可以再给我一次机会吗？”

面试官本来戏谑的笑容瞬间灿烂了起来，说：“其实我一眼看你就不简单啊哈哈！孺子可教也，那么我就再给你一次机会，这次你可要接好了！本道题目叫做：环形链表 II !

于是面试官带着笑容开始介绍起了题目~

3. 环形链表 II

链接：142. 环形链表 II

描述：

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。

不允许修改 链表。

示例1:

输入：head = [3,2,0,-4], pos = 1
输出：返回索引为 1 的链表节点
解释：链表中有一个环，其尾部连接到第二个节点。

示例2：

输入：head = [1,2], pos = 0
输出：返回索引为 0 的链表节点
解释：链表中有一个环，其尾部连接到第一个节点。

示例3：

输入：head = [1], pos = -1
输出：返回 null
解释：链表中没有环。

提示：

• 链表中节点的数目范围在范围 [0, 10^4] 内
• -10^5 <= Node.val <= 10^5
• pos 的值为 -1 或者链表中的一个有效索引

一见到这个题目，你心里一慌，但是你知道这是你最后的机会。所以你疯狂地思考。

你脑子中一时闪过了整个宇宙，又想到了 快慢指针 。

你想着：“既然是要求 链表的入环点，那么我用 环形链表 的方法找到 交点 ，我又双叒叕看过某位帅气的博主(还是我)的上一篇博客，里面有个叫做 相交链表 的问题，那么我把这个 入环的第一个节点 看作是 两个相交链表的尾结点 不就可以了，这就转换成了链表相交的问题了！我真是个天才！”

于是你自信的写下了你的思路。

思路1：

先利用 快慢指针 ，以 环形链表 的解法，找到 fast 和 slow 相交的点。然后将这个 交点 给为 meetnode 。作为两条新链表的尾。那么 meetnode->next 为某条新链表的头。然后 入环点 ，就可以看做是两条链表的交点。

然后就是 相交链表 的做法，我就不多赘述了~

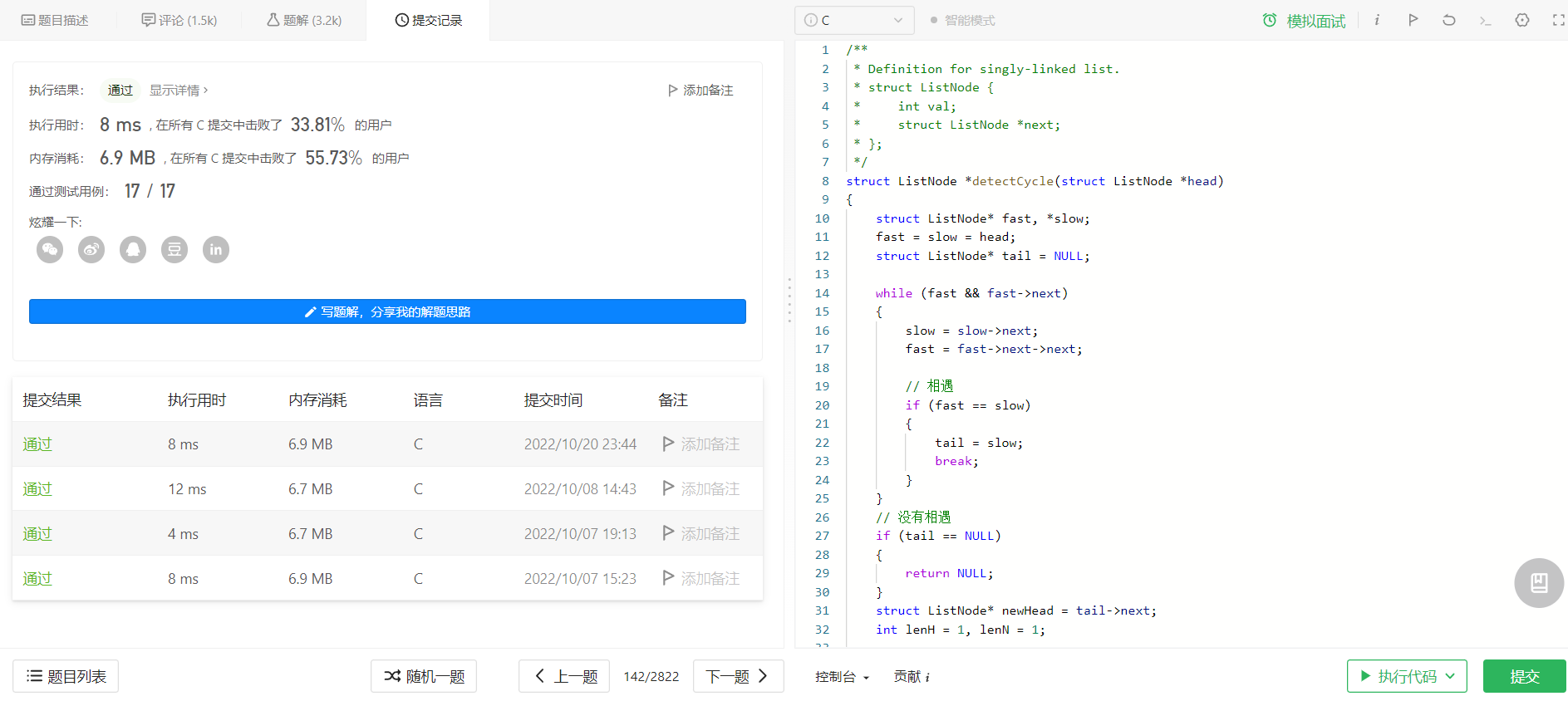
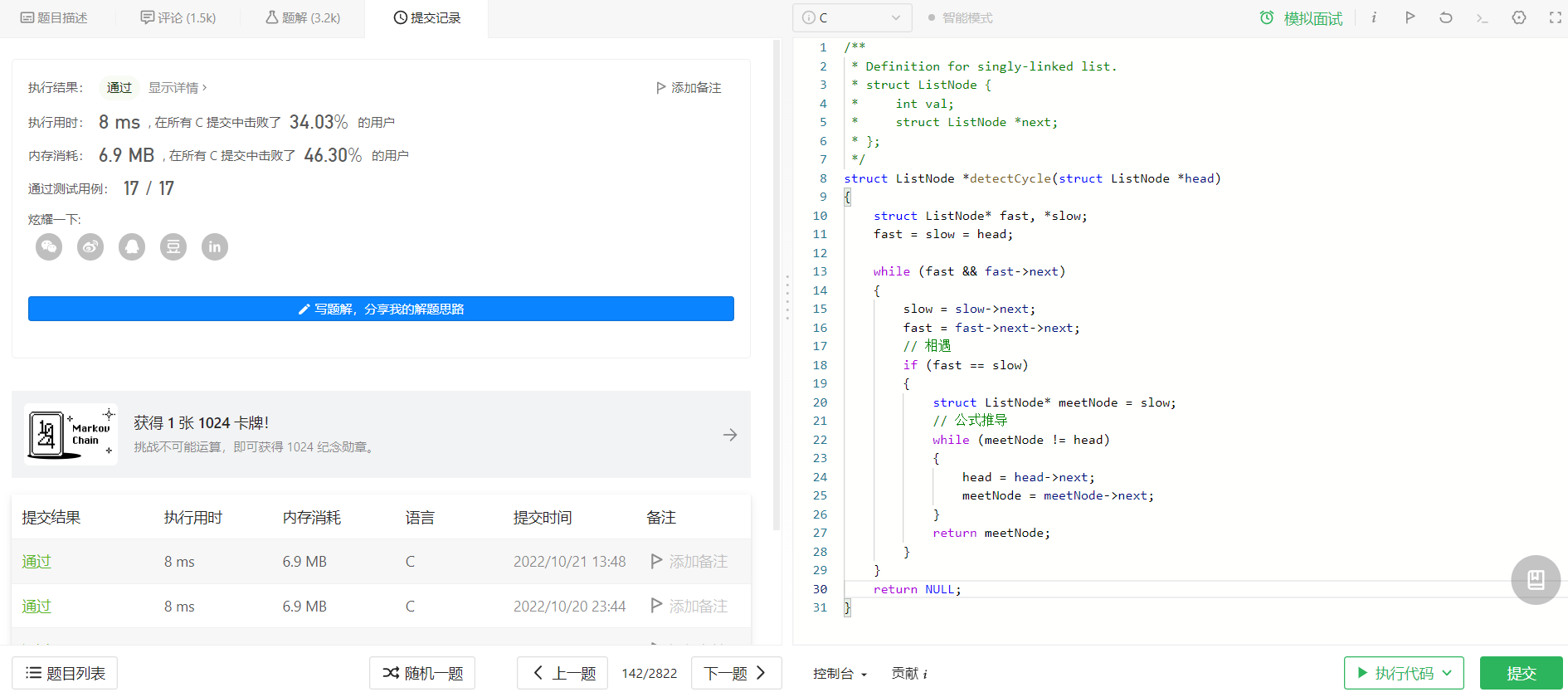
代码：

struct ListNode *detectCycle(struct ListNode *head) 
{
    struct ListNode* fast, *slow;
    fast = slow = head;
    struct ListNode* tail = NULL;
    while (fast && fast->next)
    {
        slow = slow->next;
        fast = fast->next->next;

        // 相遇
        if (fast == slow)
        {
            tail = slow;
            break;
        }
    }
    // 没有相遇
    if (tail == NULL)
    {
        return NULL;
    }
    struct ListNode* newHead = tail->next;
    int lenH = 1, lenN = 1;
    struct ListNode* curH = head, *curN = newHead;
    while (curH != tail)
    {
        lenH++;
        curH = curH->next;
    }
    while (curN != tail)
    {
        lenN++;
        curN = curN->next;
    }
    struct ListNode* longList = lenH > lenN ? head : newHead;
    struct ListNode* shortList = lenH > lenN ? newHead : head;
    int gap = abs(lenH - lenN);
    while (gap--)
    {
        longList = longList->next;
    }
    while (longList != shortList)
    {
        longList = longList->next;
        shortList = shortList->next;
    }    
    return longList;
}

面试官看了你的做法，点点头，说：“小伙子很不错嘛！知道举一反三！看在你这么聪明的份上，我再教你个厉害的！怎么样？”

你点点头，于是面试官开始了他的讲解。看思路2↓

---

思路2(精讲)：

面试官拿着笔，在纸上写下了三个大字：“公式法。”

面试官举着笔，不可一世地说：“这个方法的难点在于公式推导的过程，只要推导出了公式，解题就变得十分简单。”

然后眉飞色舞地继续说：“先把结论告诉你吧：一个指针从 相遇点 开始走，一个指针从 链表头 开始走，它们会在 环的入口点 相遇。”

接下来，就让我来为你推导公式：

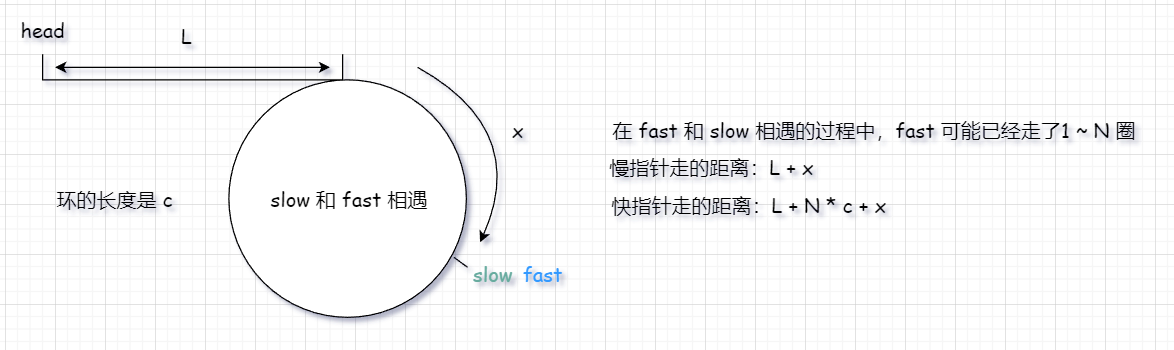
由于 fast 的速度是 slow 的 2 倍。

所以便可以得出这个式子：2 ( L + x ) = L + N * c + x，而这个式子又可以进行推导：

2 ( L + x ) = L + N * c + x
            ↓
      L + x = N * c
            ↓
      L = N * c - x
            ↓
      L = ( N - 1 ) * c +  c - x 

其实这里 公式已经推导 完成：L = ( N - 1 ) * c + c - x 。但是这个公式到底是什么意思？

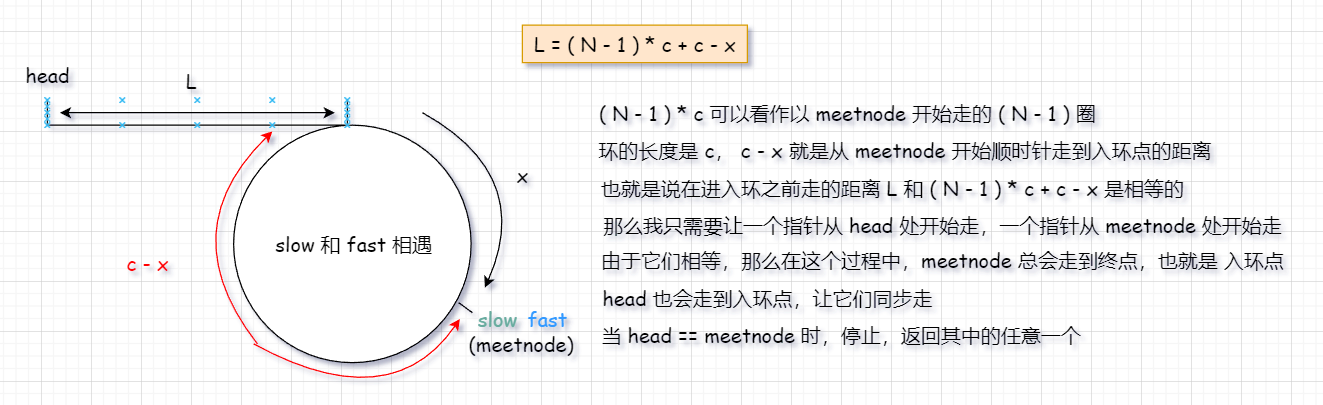
根据这个我们也就可以做出这道题目了。

讲完，面试官得意地笑着说：“怎么样，同学？你学会了吗？”

你说：“学废了学废了，我感觉我的链表水平更上一层楼~” 但是说完你又感觉到了不对劲，面试官又展现出他邪魅的笑容。

面试官说：“那么你很懂咯，你只要再把这道题目写出来，你就通过本次面试！怎么样，你有信心吗？”

你内心略微慌张，但是表面稳如老狗，说到：“来吧！”

“好的，接下来，这道题目叫做：复制带随机指针的链表！”

4. 复制带随机指针的链表

链接：138. 复制带随机指针的链表

描述：

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

val：一个表示 Node.val 的整数。
random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。
你的代码 只 接受原链表的头节点 head 作为传入参数。

示例1：

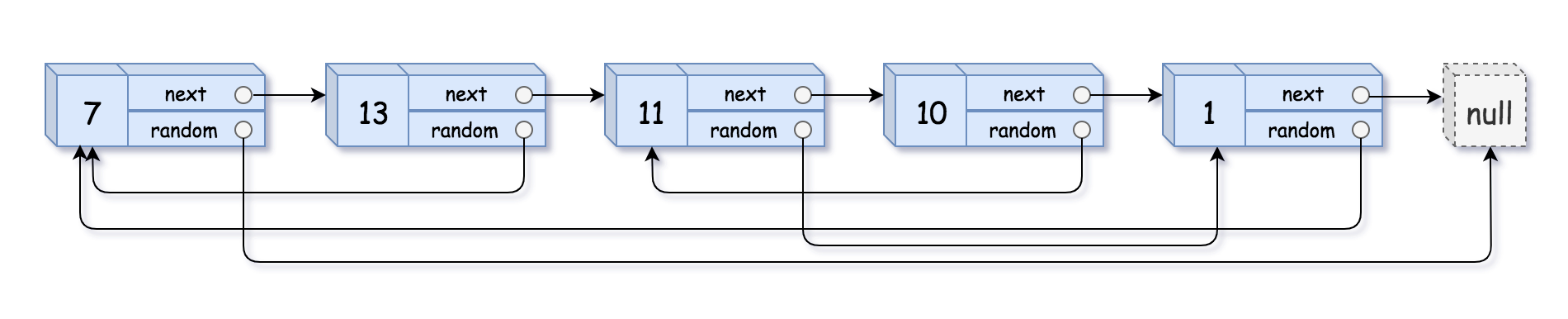
输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

提示：

• 0 <= n <= 1000
• -10^4 <= Node.val <= 10^4
• Node.random 为 null 或指向链表中的节点。

看到这道题目后，你的第一感觉是，这个链表结构含有 三个成员 ：

struct Node
{
  	int val;
    struct Node* next; // 下一个节点的地址
    struct Node* random; // 指向随机节点的指针
};

然后你看到 复制 两字，你和面试官说：“这不是只要复制原链表的每个节点，将其链接起来不就行了？”

面试官听到这句话，优哉游哉地问：“那你的 random 呢？这个你怎么复制？”

你一听，顿时感觉有点心慌。心里想：“对啊，这道题目哪有这么简单。题目里说了它是 深拷贝 ，那么就应该完全复刻啊！并且我即使知道了原链表中和 random 链接的节点，我也不知道 random 和它的相对位置啊！这到底该咋办？”

面试官试着引导你的思路：“不知道你有没有这样的经历，我之前高中上英语课老师要求我们当场写阅读理解时，我虽然有答案。可这答案可不是那么好 copy 的。“

面试官拿起水杯，喝了口水，继续说：“为了不让老师发现，你得在原题目后 偷偷 写上答案。虽然你知道答案，但是你 找不到答案的位置 啊，所以你还得 通过 这份答案，画出答案所在的位置。然后为了防止老师发现你 copy 的痕迹，你得将你 copy 的答案和你划出的答案位置 串联 起来，并且抹除 掉之前的痕迹。你之前有过这样吗？”

你一听，恍然大悟，说到：“哦！我明白了！偷偷写上答案 是我可以在原链表中每个节点的后面，复制这个节点，插入到原节点和下一个节点之间；通过答案画出答案所在的位置 就相当于我知道 复制的节点是在原节点的后面 ，那么如果我已经知道原节点的 random 那么我 复制节点的 random 不就是 原节点的random的next节点？串联答案，抹除痕迹 就是将 复制节点 链接为新链表，和原链表断开链接，恢复原链表！我悟了！”

面试官听了点了点头，说道：“请开始你的表演！友情提示，虽然你的思路差不多对了，但是注意把控细节哦~”

思路(精讲)：

思路其实在上面已经描述的差不多了，所以这里说一下细节。

首先，我们给定一个 copy 节点。在原链表每个节点的后面和这个节点的下一个节点之间插入 copy 节点。

这里就对细节有一定的要求。我们就把遍历原链表的节点叫做 cur 吧。

如果 cur 为空，则不进行拷贝。我们插入的 copy 节点是 动态开辟 的。我们需要将 copy 链接到 cur->next ，然后在让 cur->next 给定为 copy 。随后 cur 就需要原节点的后方，也就是当前 copy 节点的 next 。这就考察了 任意插入元素。

其次，根据原节点 random ，处理 copy 节点的 random 。

其实我们现在已经将 copy 节点和 原链表建立了联系。

原链表的 random 为 cur->random 、而我们插入的 copy 节点也需要链接。如果我们原链表的当前节点的 random 为 cur->random ，那么我的 copy 节点的 random 节点的相对位置应该和当前节点相同。而我们的当前节点的 random 的后方的 拷贝节点 就是这个 copy 节点的 random 。那么我 copy->random 就等于 cur->random->next 。这样不就链接起来了？

这过程中只要处理好迭代关系就可以了，但是需要注意，当 random 指向为 NULL 时，拷贝处也为 NULL。

最后，复制节点链接为新链表，原链表恢复。

完成这一步，我们需要 copyhead 和 copytail 作为复制链表的头和尾。

而复制节点链接为新链表的过程实际上就是 尾插 。所以要注意一下 空链表尾插 和 正常尾插 的情况。

并且在这过程中，将原链表的链接逐渐恢复，这些就需要自己把控了~

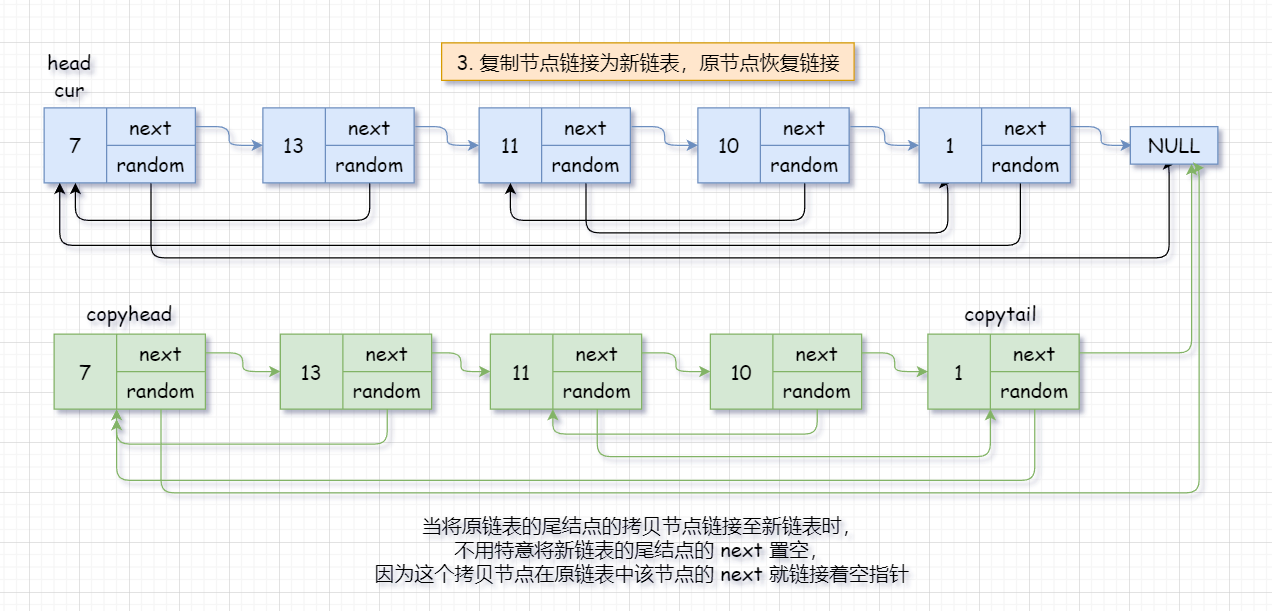
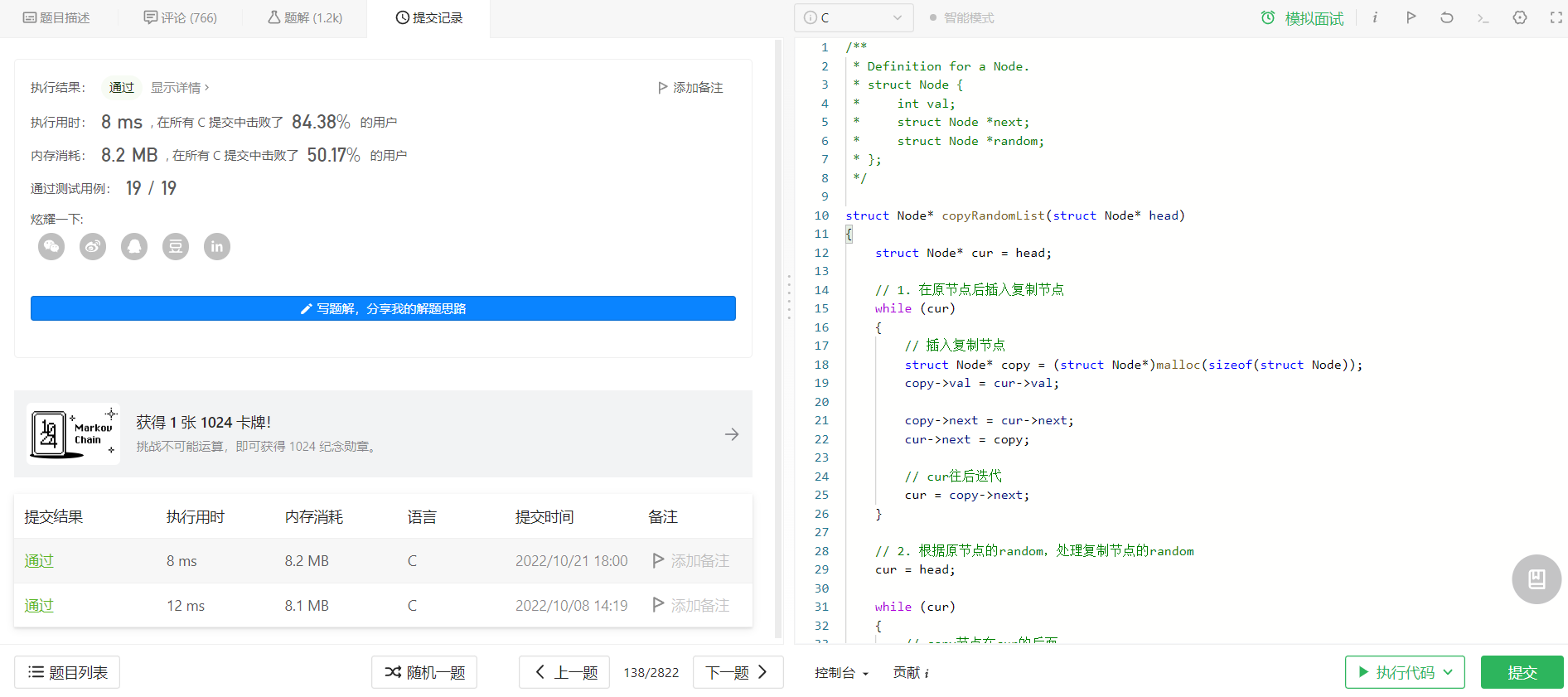
代码：

/**
 * Definition for a Node.
 * struct Node {
 *     int val;
 *     struct Node *next;
 *     struct Node *random;
 * };
 */

struct Node* copyRandomList(struct Node* head) 
{
	struct Node* cur = head;

    // 1. 在原节点后插入复制节点
    while (cur)
    {
        // 插入复制节点
        struct Node* copy = (struct Node*)malloc(sizeof(struct Node));
        copy->val = cur->val;
       
        copy->next = cur->next;
        cur->next = copy;

        // cur往后迭代
        cur = copy->next;
    }

    // 2. 根据原节点的random，处理复制节点的random
    cur = head;

    while (cur)
    {
        // copy节点在cur的后面
        struct Node* copy = cur->next;

        if (cur->random == NULL)
        {
            copy->random = NULL;
        }
        else
        {
            copy->random = cur->random->next;
        }

        cur = copy->next;
    }

    // 3. 复制节点链接为新链表，原节点恢复

    struct Node* copyHead = NULL, *copyTail = NULL;
    cur = head;

    while (cur)
    {
        struct Node* copy = cur->next;
        struct Node* next = copy->next;// 记录原链表的下一个节点

        // 复制节点链接为新链表(本质为尾插)
        if (copyTail == NULL)
        {
            copyHead = copyTail = copy;
        }
        else
        {
            copyTail->next = copy;
            copyTail = copy;
        }

        cur->next = next;// 恢复链接
        cur = next;
    }
    return copyHead;
}

解完这道题目后，你自信地说：“面试官，你看我行吗？”

面试官笑着说：“哈哈哈，小伙子厉害呀！我为你点赞！本次面试你通过了，回去等通知吧！💇‍♂”

5. 结语

到这里本篇博客就到此结束了。

说真的，博主还是第一次以这种形式写博客，不知道大家的观感如何。希望这篇博客能帮助大家理解这些OJ题，因为 环形链表系列问题 是十分经典的面试题，而普通的讲解我感觉过于生涩，这样可能更容易理解一些，而且偶尔皮一下还是很不错的(doge)。

还是老规矩，大家在看完这些题目后还是亲自去画画图，实践一下。多写多练才能学好数据结构。

这期结束，链表OJ也就到此收官了。之后我会陆续为大家带来博主在学习数据结构时总结的知识点，更多精彩内容，敬请期待~

如果觉得anduin写的还不错的话，还请一键三连！如有错误，还请指正！

我是anduin，一名C语言初学者，我们下期见！