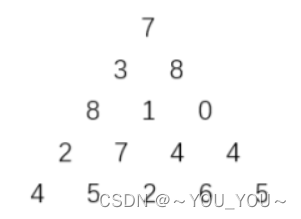
上图给出了一个数字三角形。从三角形的顶部到底部有很多条不同的路径。对于每条路径，把路径上面的数加起来可以得到一个和，你的任务就是找到最大的和。

路径上的每一步只能从一个数走到下一层和它最近的左边的那个数或者右 边的那个数。此外，向左下走的次数与向右下走的次数相差不能超过 1。

输入描述

输入的第一行包含一个整数 N\ (1 \leq N \leq 100)N (1≤N≤100)，表示三角形的行数。

下面的 NN 行给出数字三角形。数字三角形上的数都是 0 至 100 之间的整数。

输出描述

输出一个整数，表示答案。

输入输出样例

示例

输入

5
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5

输出

27

运行限制

• 最大运行时间：1s
• 最大运行内存: 256M

 解题思路：

1.递归法

  public static int dfs(int[][] arr, int i, int j){

    if(i == arr.length-1){
        return arr[i][j];
    }

    int x = dfs(arr,i+1,j);
    int y = dfs(arr,i+1,j+1);

    return Math.max(x,y)+arr[i][j];

}

递归法是我最开始想到的方法。通过分治的思想，把很大的三角形看成两层的三角形，比较下一层两个数的大小，最后加上顶层的数，便能解决问题。

但是在蓝桥杯的判定上出现了段错误。

2.动态规划

由于在蓝桥杯的判定上出现了段错误，所以我又想到了采用动态规划来解决问题。

//采用动态规划问题
    /*
    定义一个二维数组maxSum跟最原先的数组大小一样
    最后一行相等，随后往上一行的数都是下一行的数两两比较的最大值加上原本数列arr[i][j]的值     maxSum[i][j] = Math.max(maxSum[i+1][j],maxSum[i+1][j+1]) + arr[i][j] 
    maxSum[i][j]三角形顶点便是最优解
     */
    public static int max(int[][] arr){
        int n = arr.length;
        int[][] maxSum = new int[n][n];
        int max ;
        if (n - 1 >= 0) System.arraycopy(arr[n - 1], 0, maxSum[n - 1], 0, n - 1);
//        for (int i = 0; i < arr.length-1; i++) {
//            maxSum[arr.length-1][i] = arr[arr.length-1][i];
//        }

        for (int i = n-1; i > 0 ; i--) {
            for (int j = 0 ; j < i; j++) {
                    maxSum[i-1][j] = Math.max(maxSum[i][j],maxSum[i][j+1]) + arr[i-1][j];
            }
        }
        return maxSum[0][0];
    }

完整代码如下

public class sanjiaoxing {
    public static void main(String[] args) {

        Scanner scanner = new Scanner(System.in);

        int num = scanner.nextInt();
        int[][] arr = new int[num][num];
        for (int i = 0; i < num; i++) {
            for (int j = 0; j <= i; j++) {
                arr[i][j] = scanner.nextInt();
            }
        }
//        for (int[] ints : arr) {
//            for (int j = 0; j < arr.length; j++) {
//                System.out.print(ints[j] + " ");
//            }
//            System.out.println();
//        }
//        int num_1 = dfs(0,0);
        int max = max(arr);
        System.out.println(max);

    }

//    public static void max(int i, int j, int left,int right,int sum){
    //在蓝桥杯官网上运行不了，段错误，所以使用其他写法
      public static int dfs(int[][] arr, int i, int j){

        if(i == arr.length-1){
            return arr[i][j];
        }

        int x = dfs(arr,i+1,j);
        int y = dfs(arr,i+1,j+1);

        return Math.max(x,y)+arr[i][j];

    }


    //采用动态规划问题
    /*
    定义一个二维数组跟最原先的数组一样
    最后一行相等，随后往上都是下一行的两两比较的最大值加上原本数列的值 maxSum[i][j] = Math.max(maxSum[i+1][j],maxSum[i+1][j+1]) + arr[i][j] 最上一个便是最优解
     */
    public static int max(int[][] arr){
        int n = arr.length;
        int[][] maxSum = new int[n][n];
        int max ;
        if (n - 1 >= 0) System.arraycopy(arr[n - 1], 0, maxSum[n - 1], 0, n - 1);
//        for (int i = 0; i < arr.length-1; i++) {
//            maxSum[arr.length-1][i] = arr[arr.length-1][i];
//        }

        for (int i = n-1; i > 0 ; i--) {
            for (int j = 0 ; j < i; j++) {
                    maxSum[i-1][j] = Math.max(maxSum[i][j],maxSum[i][j+1]) + arr[i-1][j];
            }
        }
        return maxSum[0][0];
    }
}