目录
二叉树的基本概念
定义:
二叉树是一个由结点构成的有限集合,这个集合或者为空,或者由一个根结点及两棵互不相交的分别称作这个根的左子树和右子树的二叉树组成。当二叉树的结点集合为空时,称为空二叉树。
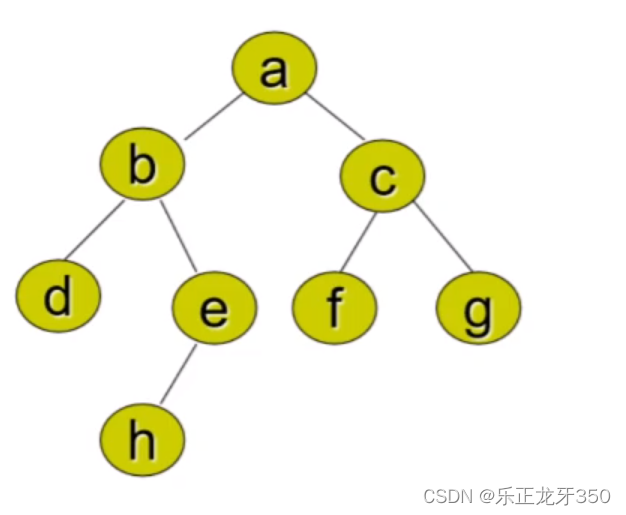
二叉树与一般树型结构的主要区别在于:
- 二叉树中每个非空结点最多只有两个子女,而一般的树形结构中每个非空结点可以有0到多个子女
- 二叉树中结点的子树要区分左子树和右子树,即使在结点只有一棵子树的情况下也要明确指出左子树还是右子树。
二叉树具有一下重要性质:
- 一棵非空二叉树的第i层上至多有
 个结点(i>.=1)
个结点(i>.=1) - 深度为h的二叉树至多有
 个结点
个结点 - 对于任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数n2,则n0=n2+1
- 性质3推论:n=n0+n1+n2,n0+n1+n2=n1+2*n2+1
完全二叉树
如果一棵二叉树扣除其最大层次那层后即成为一棵满二叉树,且层次最大那层的所有结点均靠左,则称原来的二叉树为完全二叉树
满二叉树
如果一棵二叉树中所有终端结点均位于同一层次,其它非终端结点的度数均为2,则称此二叉树为满二叉树
完全二叉树的性质
对于具有n个结点的完全二叉树,如果按照从上到下、同一层次上的结点按从左到右的顺序对二叉树中的所有结点从1开始顺序编号,则对于序号为i的结点有:
- 如果i>1,则序号为i的结点其双亲结点的序号为 i/2向上取整 如果结点i为根结点,没有双亲;
- 如果2i>n,则结点i无左子女;否则其左子女结点为2i
- 如果2i+1>n,则结点i无右子女;否则其右子女为结点2i+1
二叉树的存储结构
存储结构有两种:顺序存储结构和链式存储结构
顺序存储结构
顺序存储结构是使用一组连续的空间存储二叉树的数据结构元素和数据元素之间的关系。因此必须将二叉树中所有的结点排成一个适当的线性序列,在这个线性序列中应采用有效的方式体现结点之间的逻辑关系。
完全二叉树的顺序存储
#define MAXSIZE 20
typedef char datatype;
datatype tree[MAXSIZE];
int n;
一般二叉树的顺序存储
由于二叉树中每个结点最多只有两个子女,于是存储一个结点时,除了包含结点本身的属性外,另外增加两个域,分别用来指向该结点的两个子女在数组中的下标。
一般二叉树顺序存储数据结构的定义如下
#define MAXSIZE 20
typedef char datatype;
typedef struct {
datatype data;
int lchild,rchild;
}node;
node tree[MAXSIZE];
int n;
int root;链式存储结构
二叉树的链式存储方式下每个结点也包含三个域,分别记录该结点的属性值及左、右子树的位置。与顺序存储结构不同的是,其左、右子树的位置不是通过数组的下标,而是通过指针的方式体现。
链式存储方式下二叉树结点数据结构的定义如下
typedef char datatype;
typedef struct node{
datatype data;
struct node *lchild,*rchild;
}bintnode;
typedef bintnode *bintree;
bintree root;链式存储方式下带双亲结点指针的二叉树结点数据结构的定义如下
typedef char datatype;
typedef struct node{
datatype data;
struct node *lchild,*rchild;
struct node *parent;
}bintnode;
typedef bintnode *bintree;
bintree root;二叉树的遍历
二叉树遍历的定义
二叉树的遍历是指按一定的顺序对二叉树中的每一个结点均访问一次,且仅访问一次
遍历分为三种:前序遍历、中序遍历和后序遍历
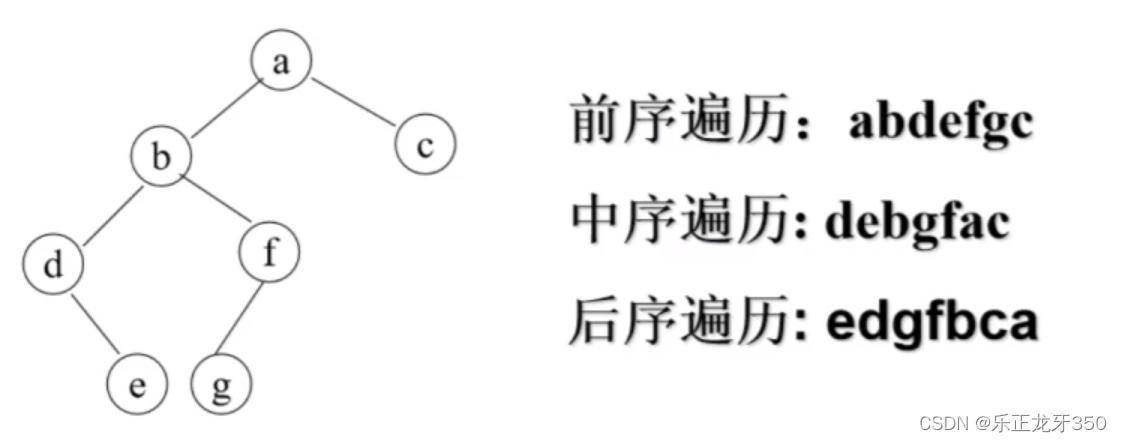
前序遍历:首先访问根结点,然后访问根结点的左子树,最后访问根结点的右子树。
中序遍历:首先访问根结点的左子树,然后访问根结点,最后访问根结点的右子树。
后序遍历:首先访问根结点的左子树,然后访问根结点的右子树,最后访问根结点。
范例如下图:
前序遍历二叉树的递归算法
void preorder(bintree t)
{
if(t)
{
printf("%c",t->data);
preorder(t->lchild);
preorder(t->rchild);
}
}中序遍历二叉树的递归算法
void inorder(bintree t)
{
if(t)
{
inorder(t->lchild);
printf("%c",t->data);
inorder(t->rchild);
}
}后序遍历二叉树的递归算法
void postorder(bintree t)
{
if(t)
{
postorder(t->lchild);
postorder(t->rchild);
printf("%c",t->data);
}
}二叉树的创建算法
利用二叉树前序遍历的结果可以非常方便地生成给定的二叉树,具体做法是:将第一个输入的结点作为二叉树的根结点,后继输入的结点序列是二叉树左子树前序遍历的结果,由它们生成的二叉树的左子树;在接下来输入的结点序列为二叉树右子树前序遍历的结果,应该有它们生成二叉树的右子树。
注:遍历中遇到空子树时,用‘#’代替
bintree creatbintree()
{
char ch;
bintree t;
if(ch=getchar()=='#') t=NULL;
else
{
t=(bintnode*)malloc(sizeof(bintnode));
t->data=ch;
t->lchild=creatbintree();
t->rchild=creatbintree();
}
return t;
}二叉树的非递归实现
采用非递归方式实现二叉树遍历时,必须使用一个堆栈记录回溯点,以便将来进行回溯。以下为一个顺序栈的定义及部分操作的实现
顺序栈头文件
typedef struct stack //栈结构的定义
{
bintree data[100]; //为栈中每个元素设置的标记,用于后序遍历
int tag[100];
int top; //栈顶指针
}seqstack;进栈
void push(seqstack *s,bintree t)
{
s->data[s->top]=t;
s->top++;
}出栈
bintree preorder(seqstack *s)
{
if(s->top!=0)
{
s->top--;
return (s->data[s->top]);
}
else return NULL;
}非递归实现二叉树的前序遍历
void preorder1(bintree t) //非递归实现二叉树的前序遍历
{
seqstack s;
s.top=0;
while((t) || (s.top!=0)) //当前处理的子树不为空或栈不为空则循环
{
printf("%c",t->data);
push(&s,t);
t=t->rchild;
}
}二叉树中序遍历的