作者 | Simon 仿真秀优秀讲师
导读:在一些船舶,例如客船和客滚船的结构设计中,经常接触到比较“薄”的板。而目前规范对于板的屈曲校核普遍采用较为“统一”的方法,并未对“薄板”与“厚板”做区分。那对于“薄板”,我们现有的规范适用吗?笔者最近读到一本书《Trends in Analysis and Design of Marine Structures》,书中文章结合试验,研究了薄板的屈曲性能,很有意思。笔者结合自己对屈曲、薄板屈曲的理解和大家一起对这个问题做一次讨论。
一、提出问题
近年来,随着规范越来越复杂,计算工况越来越多,屈曲校核过程有“流程化”、“无脑化”的趋势,用工程软件自动加载、校核而后看“红绿灯”是常规操作。借“薄板”这个话题来重新思考一下屈曲问题,相信会有所收获。同样的,课本知识 + 梁理论 + 有限元的组合拳是我们分析和研究的利器。在展开讨论之前,有几个问题可以帮助大家思考:
- 1) 多厚是“厚”,多薄是“薄”?
- 2) 书本如何推导板格的纵向屈曲?
- 3) 规范是如何规定板的屈曲能力的?
这里,笔者抛砖引玉给出一些参考。问题1):首先板的厚与薄是相对的,我们要引入合适的无量纲参数作为比较。从书本中可知一般情况下纵骨架式板格的(欧拉)纵向屈曲应力可表示为
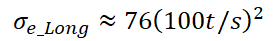
t为板厚,s为骨材间距。可见,t/s是一个直接平方关系影响屈曲强度的无量纲数。板的厚与薄应该从t/s来考虑。而船舶海洋工程结构物,s一般在500mm到800mm的范围,常规t从5mm到30mm的范围。规范中对屈曲问题,考虑到建造、初始缺陷、焊接应力、破环案例、材料等等因素,公式也复杂一些。规范的无量纲参数β考虑了材料的屈服应力和杨氏模量:
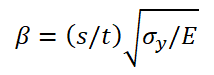
可见,s一定时,t越小,β越大。一般油船、散货船的β都在3以下,而客船、客滚船的β可达3~5甚至更大到6。我们可以以β = 3为线区分所谓的“薄”和“厚”。另外,需要注意规范定义的初始缺陷的上限亦以s为基准(而不是t,如下图所示),为s/200。这点比较容易被忽略,但它是屈曲分析的一大前提,后面将展开讨论。
问题2)翻阅书本可知,板的稳定性问题是分两步走的,临界(弹性)屈曲和后屈曲。板的临界屈曲求解是从板的中性平衡微分方程(即板在面外载荷q作用下的弯曲问题)入手的。然后考虑板的中性面受压力和剪力,并令q=0,求解板的平衡解。这与求解压杆稳定性,从梁的复杂弯曲入手,套路是一样的。公式推导这里不再列举,这里是笔者自己对书本内容的工程理解,仅供参考和讨论,也欢迎指正理解不到位的地方。
- (1)板在中面受压时,除了在受压方向上的中面“压缩”这个“解”之外,(数学上)在一定条件下还能“触发”面外方向上的“解”,即板“拱”或“凹凸”起来。
- (2)这个条件由压载荷的值达到一定大小后“触发”。压杆表达为欧拉力公式,板表达为欧拉应力公式,弹性范围内是仅和几何和材料弹性模量、泊松比有关的值。
- (3)与中面压缩这个解不同,面外方向上的“解”一旦触发,板格即失去稳定性。这个可以从两方面理解,首先在数学求解上得到的只是板面外变形的“形式”,对其具体“幅值”,求解过程并无直接“限制”(可以通过引入能量法来做一定约束);从刚度上理解,板一旦出现较大的面外变形,其面内的“轴向刚度”会失去作用,而换由板的“弯曲刚度”来抵抗面内载荷,而弯曲刚度是比轴向刚度要小得多。
- (4)书本上这部分内容是从数学推导出发的,理论上适用性很广,并无“厚”和“薄”的区别。
板的后屈曲性能是区别板和压杆屈曲的重要特点,即临界屈曲后的“应力重分布”。当板格的β较大时(即所谓薄板),板格容易发生弹性屈曲,若板的边界能提供有效支撑则板格能够继续承载,此时载荷主要由靠近边界的“有效宽度”来承担直至屈服,如下图所示。
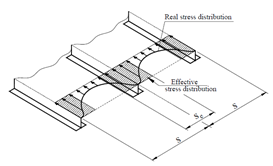
书本上将一般情况下的有效宽度假设为两边各0.22s。笔者认为其不一定适用于薄板的情况。根据截面Type III(参考DNV-OS-C101, Appendix A)的要求,取板厚的某个倍数,如15倍左右的板厚比较适合。
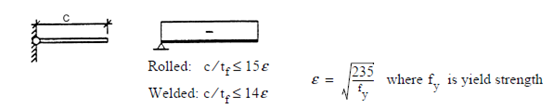
问题3)书本和规范中对于不考虑应力重分布的板,其临界应力σcr的计算分两步,先计算欧拉应力σE,它仅和几何及弹性模量E、泊松比ν有关。若σE /σy<=0.5,则σcr =σE,若σE /σy >0.5,则做修正得到σcr。即:
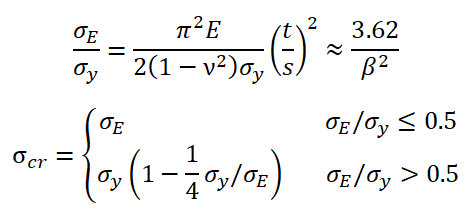
书本中,对于考虑应力重分布的板格的极限强度σu,表示为:
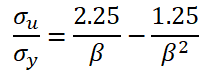
船舶共同规范CSR的定义为:
点击完整阅读全文
相关阅读推荐