堆的基本定义
定义: 堆是计算机中一种特殊的数据结构,通常被看成一颗完全二叉树的数组对象
堆的性质
性质:
1.它是完全二叉树,除了树的最后一层结点不需要是满的,其它的每一层从左到右都是满的,如果最后一层结点不 是满的,那么要求左满右不满。
2.它通常用数组来实现。 具体方法就是将二叉树的结点按照层级顺序放入数组中,根结点在位置1,它的子结点在位置2和3,而子结点的子结点则分别在位置4,5,6和7,以此类推。
3.如果一个结点的位置为k,则它的父结点的位置为[k/2],而它的两个子结点的位置则分别为2k和2k+1。这样,在不使用指针的情况下,我们也可以通过计算数组的索引在树中上下移动:从a[k]向上一层,就令k等于k/2,向下一层就令k等于2k或2k+1。
3.每个结点都大于等于它的两个子结点。这里要注意堆中仅仅规定了每个结点大于等于它的两个子结点,但这两个 子结点的顺序并没有做规定,跟我们之前学习的二叉查找树是有区别的。
堆的结构图:
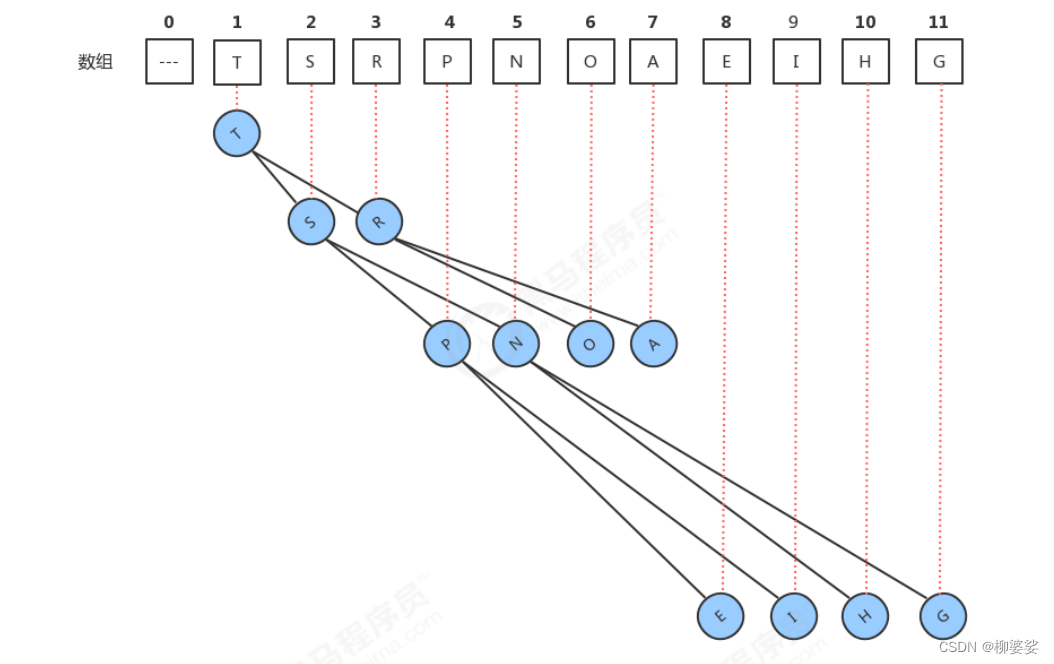
堆排序
堆排序的基本步骤
1.构造堆;
2.得到堆顶元素,这个值就是最大值;
3.交换堆顶元素和数组中的最后一个元素,此时所有元素中的最大元素已经放到合适的位置;
4.对堆进行调整,重新让除了最后一个元素的剩余元素中的最大值放到堆顶;
5.重复2~4这个步骤,直到堆中剩一个元素为止。
堆构造过程
堆的构造,最直观的想法就是另外再创建一个和新数组数组,然后从左往右遍历原数组,每得到一个元素后,添加到新数组中,并通过上浮,对堆进行调整,最后新的数组就是一个堆。
上述的方式虽然很直观,也很简单,但是我们可以用更聪明一点的办法完成它。
创建一个新数组,把原数组 0 ~ length-1的数据拷贝到新数组的1~ length处,再从新数组长度的一半处开始往1索引处扫描(从右往左),然后 对扫描到的每一个元素做下沉调整即可。
堆的插入和删除
堆的插入
往堆中插入数据,即在数组的后面加入一个数据,但插入后的数组有可能不是一个堆,需要通过 上浮 来调整,使其成为堆, 即不断的比较新结点a[k]和它的父结点a[k/2]的大小,然后根据结果完成 数据元素的交换,就可以完成堆的有序调整
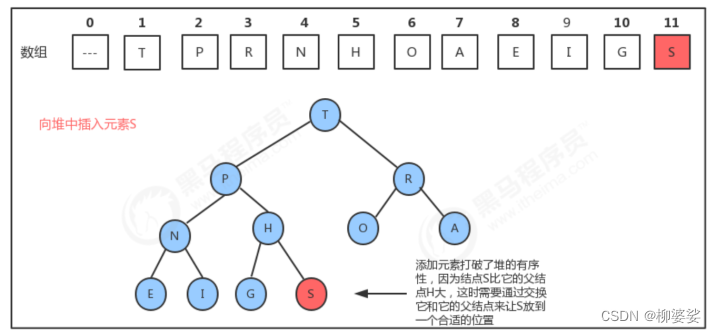
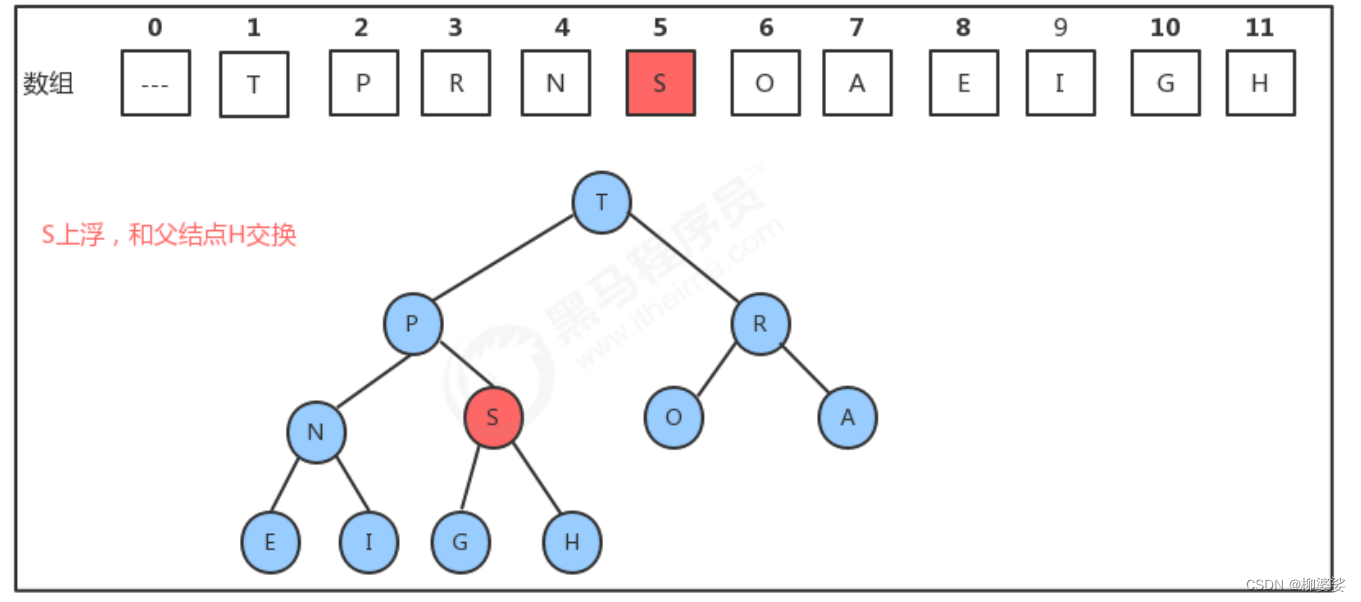
堆删除最大元素
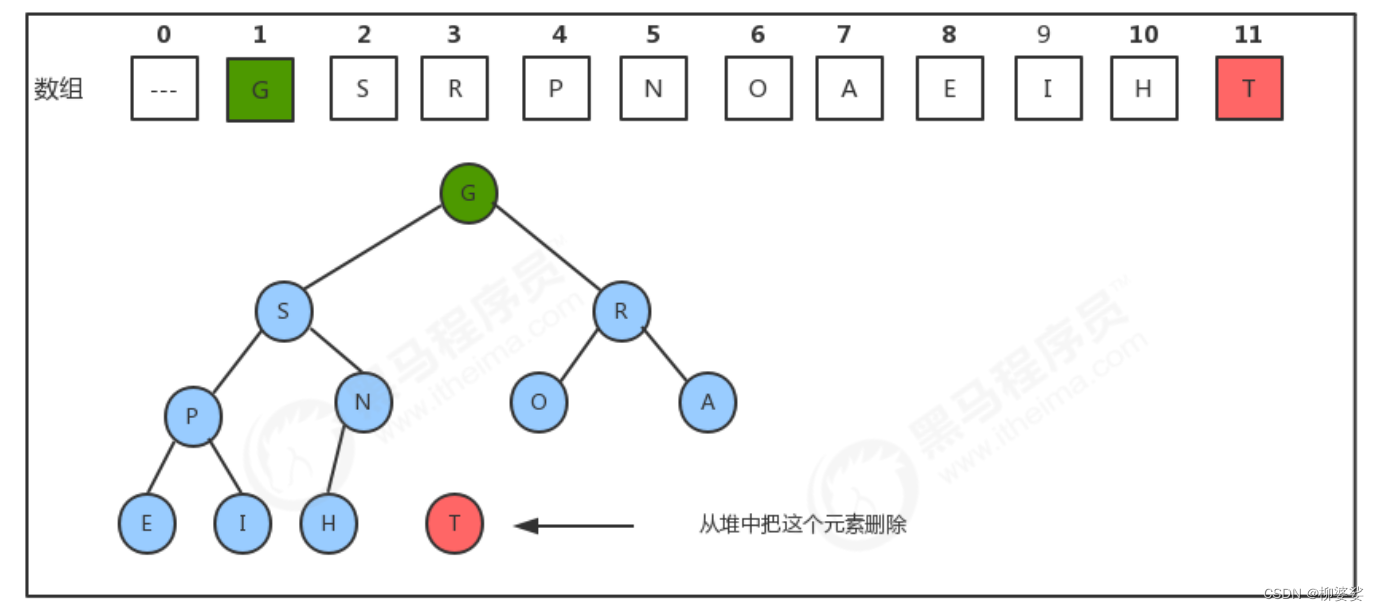
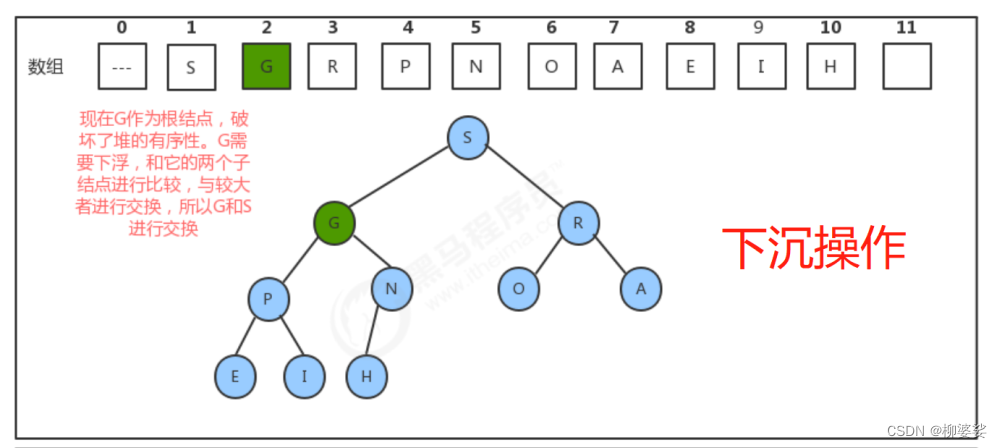
堆的最大元素,就是该完全二叉树的根节点,在数组下标为1的位置(堆是从下标为1的位置开始存放数据的);当我们把根结点的元素删除后,需要有一个新的根结点出现,这时我们可以暂时把堆中 最后一个 元素放到索引1处,充当根结点,但是它有可能不满足堆的有序性需求,这个时候我们就需要 下沉 方法,让这个新的根结点放入到合适的位置。
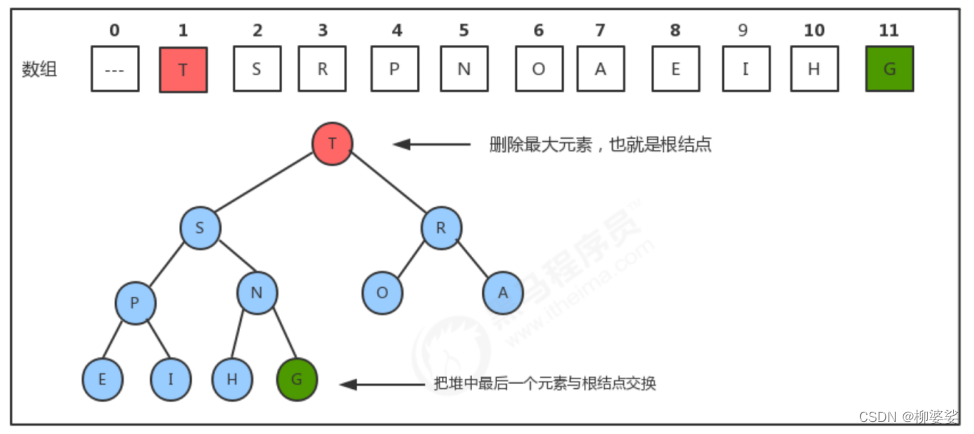
有关堆的简单知识就先到这里了,谢谢大家~