Treap树的基本操作以及模板题目

传送门：253. 普通平衡树

1.插入

2.删除

3.找前驱以及后继（找某一个节点的前驱和后继（一定存在））

4.找最大以及最小

5.求某一个值的排名

6.求排名是k的数是哪个

7.比某个数小的最大值

8.比某个数大的最小   (这个数不一定是在树中)

Treap树里面的节点定义

struct node
{
    int l,r;
    int key,val;  //key表示权值，val表示一个随机数的值，用来保持平衡树的高度不变
    int cnt,sie; //cnt表示当前节点一共有几个，sie表示以该节点为根的子树一共有多少个节点。
}tr[N];

更新当前节点的子树计数，上传信息。

void pushup(int p)
{
    tr[p].sie=tr[tr[p].l].sie+tr[tr[p].r].sie+tr[p].cnt;
}

获取一个新的节点，其中val值需要用随机数函数实现

int get_node(int key)
{
    tr[++idx].key=key;
    tr[idx].val=rand();
    tr[idx].cnt=tr[idx].sie=1;
    return idx;
}

初始化操作：

初始化一个无穷大和一个无穷小

void build()
{
    get_node(-INF),get_node(INF);
    root=1,tr[1].r=2;
    pushup(root);
    if(tr[1].val<tr[2].val) zag(root);
}

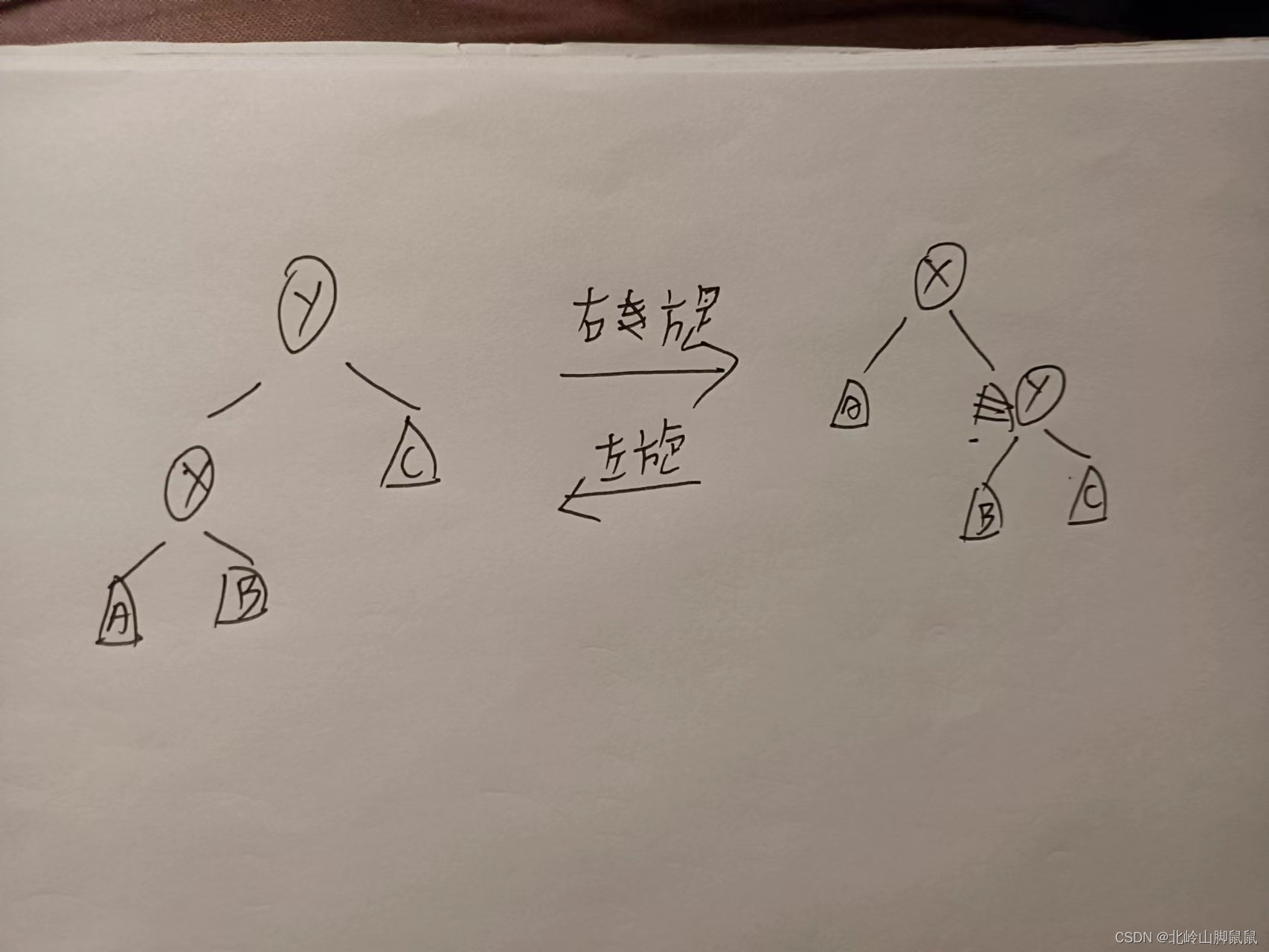
左旋，右旋操作：

操作完后是不会影响到平衡树中序遍历的顺序并且能够让父节点和子节点的位置进行交换，具体如下图所示：

中序遍历依旧是AxByC ,但是x变成了y的父节点 

代码：

void zig(int &p)//右旋
{
    int q=tr[p].l;
    tr[p].l=tr[q].r,tr[q].r=p,p=q;
    pushup(tr[p].r),pushup(p);
}
void zag(int &p) //左旋
{
    int q=tr[p].r;
    tr[p].r=tr[q].l,tr[q].l=p,p=q;
    pushup(tr[p].l),pushup(p);
}

插入操作：

void insert(int &p,int key)
{
    if(!p) p=get_node(key);  //如果树里面没有该节点就创建一个新的节点
    else if(tr[p].key==key) tr[p].cnt++;  //如果有的话就自增1
    else if(tr[p].key>key)                //如果当前节点权值大于插入权值，说明插入值应该进入左子树
    {
        insert(tr[p].l,key);   
        if(tr[tr[p].l].val>tr[p].val) zig(p); //插入后检查随机数值，如果大的话将左子树右旋上来
    }else
    {
        insert(tr[p].r,key);
        if(tr[tr[p].r].val>tr[p].val) zag(p); //同理，将右子树左旋上来
    }
    pushup(p);   //最后更新沿途节点的信息。
}

节点的删除操作：

通过不断进行左旋或者是右旋将要删除的节点下放到叶节点的位置去。

选择左旋或右旋是需要进行判断的，要保持平衡树本身性质，将左右节点中val值较大的一个节点旋转上来。保持大根堆的性质。

void remove(int &p,int key)
{
    if(!p)return ;  //如果不存在的话
    if(tr[p].key==key)   //找到了要删除的节点
    {
        if(tr[p].cnt>1) tr[p].cnt--;  //如果数量大于1，就自减1
        else if(tr[p].l||tr[p].r)  //等于1的情况下如果不是根节点
        {
            if(!tr[p].r||tr[tr[p].l].val>tr[tr[p].r].val)  //如果右子树为空或者左子树随机值比右子树大的话，两个情况都要进行右旋把左子树调上来
            {
                zig(p);
                remove(tr[p].r,key);                //要删的点下放到右子树直到变成根节点。
            }else                                    //除此之外的情况就要左旋把右子树调上来。
            {
                zag(p);
                remove(tr[p].l,key);               
            }
        }else p=0;  //如果已经是根节点就直接变成0
    }else if(tr[p].key>key) remove(tr[p].l,key); //要删的点比当前点的权值要小，说明在左子树
    else remove(tr[p].r,key);   //否则在右子树
    pushup(p);  //更新沿途节点的信息
}

汇总代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int N=1e5+10,INF=1e8;
int n;
struct node
{
    int l,r;
    int key,val;
    int cnt,sie;
}tr[N];
int root,idx;
void pushup(int p)
{
    tr[p].sie=tr[tr[p].l].sie+tr[tr[p].r].sie+tr[p].cnt;
}
int get_node(int key)
{
    tr[++idx].key=key;
    tr[idx].val=rand();
    tr[idx].cnt=tr[idx].sie=1;
    return idx;
}
void zig(int &p)//右旋
{
    int q=tr[p].l;
    tr[p].l=tr[q].r,tr[q].r=p,p=q;
    pushup(tr[p].r),pushup(p);
}
void zag(int &p)
{
    int q=tr[p].r;
    tr[p].r=tr[q].l,tr[q].l=p,p=q;
    pushup(tr[p].l),pushup(p);
}
void build()
{
    get_node(-INF),get_node(INF);
    root=1,tr[1].r=2;
    pushup(root);
    if(tr[1].val<tr[2].val) zag(root);
}
void insert(int &p,int key)
{
    if(!p) p=get_node(key);
    else if(tr[p].key==key) tr[p].cnt++;
    else if(tr[p].key>key)
    {
        insert(tr[p].l,key);
        if(tr[tr[p].l].val>tr[p].val) zig(p);
    }else
    {
        insert(tr[p].r,key);
        if(tr[tr[p].r].val>tr[p].val) zag(p);
    }
    pushup(p);
}
void remove(int &p,int key)
{
    if(!p)return ;
    if(tr[p].key==key)
    {
        if(tr[p].cnt>1) tr[p].cnt--;
        else if(tr[p].l||tr[p].r)
        {
            if(!tr[p].r||tr[tr[p].l].val>tr[tr[p].r].val)
            {
                zig(p);
                remove(tr[p].r,key);
            }else
            {
                zag(p);
                remove(tr[p].l,key);
            }
        }else p=0;
    }else if(tr[p].key>key) remove(tr[p].l,key);
    else remove(tr[p].r,key);

    pushup(p);
}



int get_rank_by_key(int p,int key) //
{
    if(!p) return 0; //不存在的话
    if(tr[p].key==key) return tr[tr[p].l].sie+1;
    if(tr[p].key>key) return get_rank_by_key(tr[p].l,key);
    return tr[tr[p].l].sie+tr[p].cnt+get_rank_by_key(tr[p].r,key);
}
int get_key_by_rank(int p,int rak)
{
    if(!p) return INF; //不存在的情况
    if(tr[tr[p].l].sie>=rak) return get_key_by_rank(tr[p].l,rak);
    if(tr[tr[p].l].sie+tr[p].cnt>=rak) return tr[p].key;
    return get_key_by_rank(tr[p].r,rak-tr[tr[p].l].sie-tr[p].cnt);
}
int get_prev(int p,int key) //严格小于key的最大数
{
    if(!p) return 0;
    if(tr[p].key>=key)  return get_prev(tr[p].l,key);
    return max(tr[p].key,get_prev(tr[p].r,key));
}
int get_next(int p,int key) //严格大于key的最小数
{
    if(!p) return INF;
    if(tr[p].key<=key) return get_next(tr[p].r,key);
    return min(tr[p].key,get_next(tr[p].l,key));
}
int main()
{
    build();
    scanf("%d",&n);
    while(n--)
    {
        int op,x;
        scanf("%d%d",&op,&x);
        if(op==1) insert(root,x);
        else if(op==2) remove(root,x);
        else if(op==3) printf("%d\n",get_rank_by_key(root,x)-1);
        else if(op==4) printf("%d\n",get_key_by_rank(root,x+1));
        else if(op==5) printf("%d\n",get_prev(root,x));
        else printf("%d\n",get_next(root,x));
    }
    return 0;
}