“算法+数据结构=程序”
这个公式对计算机科学的影响程度足以类似物理学中爱因斯坦的“E=M^2”——一个公式展示出了程序的本质。斗转星移,尽管新技术方法不断涌现,这句名言依然焕发着无限的生命力,它借助面向对象知识的普及,使数据结构技术更加完善和易于使用。由此,也说明了数据结构在计算机学科中的地位和不可替代的独特作用。
那说了这么多到底啥是数据结构嘞?
官方定义:数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
个人理解:说白了哈,数据结构就是对数据管理、存储的格式。
它包括两个层次 逻辑结构 物理结构
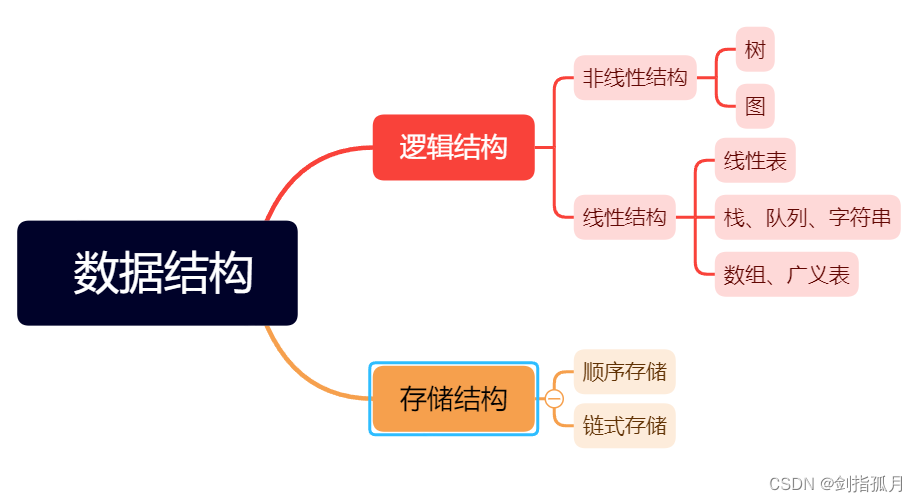
上面提到的数据结构后续会一一展开解释。
数据结构中的基本概念
数据:描述事物的符号记录。可以是音频、视频、图像、文本等
数据元素:是数据的基本单位,通常以一个整体考虑。如:李明 男 1995.2.25 江苏南京人 这样叫做一条记录,也叫一条数据元素。
数据项:是组成数据元素的不可分割的最小单位。上述中性别 即为一个数据项。
数据对象:是性质相同的数据元素的集合,是数据的一个子集。
四者关系如下: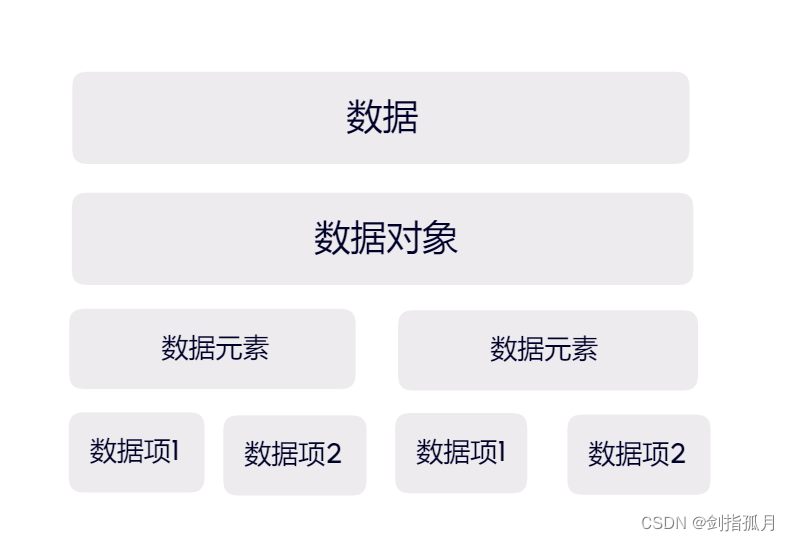
如果说数据结构是一个大舞台,那么算法就是在舞台上的表演者。
那什么算法嘞?
官方定义:算法是为了解决某类问题而规定的一个有限长的操作序列,用于解决特定的运算和逻辑问题。
算法的特性:有穷性、确定性、可行性、输入、输出。
算法就和数学上习题的解法相似,有简单的,也有复杂的,那么我们应该怎么辨别呢?
这就要说它的时间复杂度和空间复杂度了
时间复杂度是对一个算法运行时间长短的量度,也就是执行所耗费的时间成本。用大O表示,记作T(n)=O(f(n))。
常见的时间复杂度按数量级递增依次为:
常量阶O(l)、对数阶O()、线性阶O(n)、线性对数阶O(n
)、平方阶O(
)、立方阶O(
)、k次方阶O(
)、指数阶O(
) 、阶乘O(n!) 。
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度,也就是耗费空间成本。用大O表示,记作S(n)=O(f(n)).
常见的空间复杂度按数量级递增依次为:O(1)、O(n)、O(n2)等,其中递归算法的空间复杂度和递归深度成正比.
(以上仅个人理解,说的不对,请谅解并留言)