目录
LeetCode242. 有效的字母异位词
链接:242. 有效的字母异位词 - 力扣(LeetCode)
核心点:感受到 数组 用来做哈希表 给我们带来的便利。
先看暴力的解法,两层for循环,同时还要记录字符是否重复出现,很明显时间复杂度是 O(n^2)。
暴力的方法这里就不做介绍了,直接看一下有没有更优的方式。
方法:数组作哈希表
1. 思路
先看暴力的解法,两层for循环,同时还要记录字符是否重复出现,很明显时间复杂度是 O(n^2)。
暴力的方法这里就不做介绍了,直接看一下有没有更优的方式。
数组其实就是一个简单哈希表,而且这道题目中字符串只有小写字符,那么就可以定义一个数组,来记录字符串s里字符出现的次数。
需要定义一个多大的数组呢,定一个数组叫做record,大小为26 就可以了,初始化为0,因为字符a到字符z的ASCII也是26个连续的数值。
Example:为了方便举例,判断一下字符串s= "aee", t = "eae"。
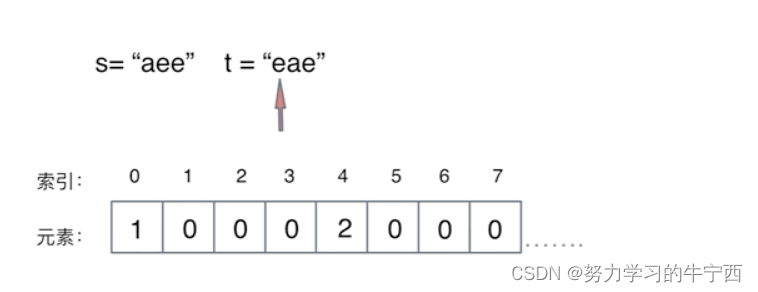
定义一个数组叫做record用来上记录字符串s里字符出现的次数。
需要把字符映射到数组也就是哈希表的索引下标上,因为字符a到字符z的ASCII是26个连续的数值,所以字符a映射为下标0,相应的字符z映射为下标25。
再遍历 字符串s的时候,只需要将 s[i] - ‘a’ 所在的元素做+1 操作即可,并不需要记住字符a的ASCII,只要求出一个相对数值就可以了。 这样就将字符串s中字符出现的次数,统计出来了。
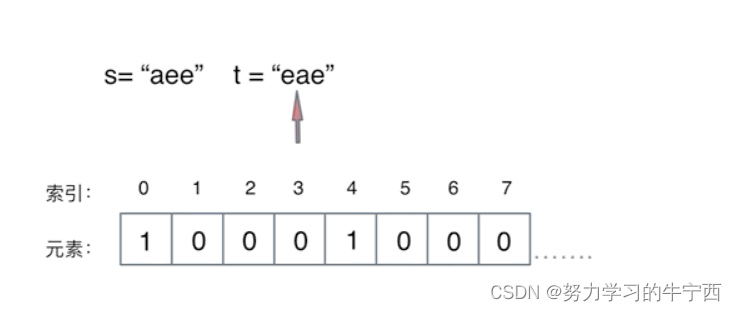
那看一下如何检查字符串t中是否出现了这些字符,同样在遍历字符串t的时候,对t中出现的字符映射哈希表索引上的数值再做-1的操作。
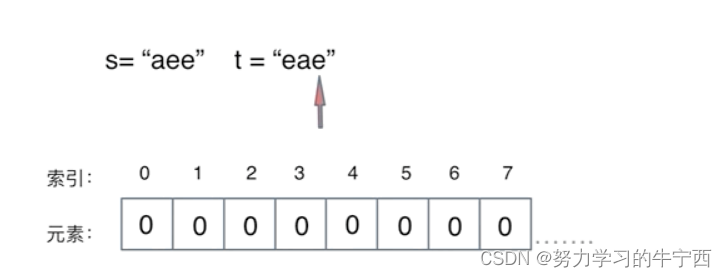
那么最后检查一下,record数组如果有的元素不为零0,说明字符串s和t一定是谁多了字符或者谁少了字符,return false。
最后如果record数组所有元素都为零0,说明字符串s和t是字母异位词,return true。
2. 代码实现
class Solution(object):
def isAnagram(self, s, t):
"""
:type s: str
:type t: str
:rtype: bool
"""
# 数组作哈希表,记录元素出现的频率
record = [0]*26
# 遍历字符串S,在每个对应位置上+1
for item in s:
index = ord(item) - ord("a")
record[index] += 1
# 遍历字符串T,在每个对应位置上-1
for item in t:
index = ord(item) - ord("a")
record[index] -= 1
# 看看最后的哈希表是不是元素全为0
for i in range(0,26):
if record[i] != 0:
return False
return True3. 复杂度分析
因为要分别遍历长度为N的字符串s和t,所以时间复杂度为O(n),空间上因为定义是的一个常量大小的辅助数组,所以空间复杂度为O(1)。
4. 思考
(1)常用的三种哈希表有数组、set和map,当哈希表比较小并且范围确定的时候,用数组;当哈希表范围比较大而且不确定的时候,用set;当有key-value的映射关系的时候,用map。
(2)在C++ 中,直接用字母减字母的话,编译器会自动用字母的ASCII码计算,但是在Python中要用ord(“a”),我们并不用搞清楚ASCII码究竟是多少,只用知道这26个字母是连续的,然后减去”a”的ASCII码,算出一个相对位置就可以了。
(3)还有另一种做法是,把两个字符串分别用两个数组统计,然后再比较两个数组是否一样。
(4)这道题是数组在Hash Map中的经典应用。
(5)思考:我们遇到要快速判断元素是否出现在集合里的时候,要考虑哈希法。
(6)数组就是简单的哈希表,但是数组的大小可不是无限开辟的。
本题学习时间:55分钟
Leetcode349. 两个数组的交集
链接: 349. 两个数组的交集 - 力扣(LeetCode)
这道题用暴力的解法时间复杂度是O(n^2),那来看看使用哈希法进一步优化。
思考:
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。
方法一:用Set作HashMap
1. 思路
本题其实是使用set的好题,但是后来力扣改了题目描述和 测试用例,添加了 0 <= nums1[i], nums2[i] <= 1000 条件,所以使用数组也可以了,我们可以先忽略这个条件,尝试去用set解决这道题目。
数据结构的选择?要不要用数组作为Hash table?为什么要用set作哈希表?
用数组来做哈希表是不错的选择,例如,前一道题:有效的字母异位词
但是要注意,使用数组来做哈希的题目,是因为题目都限制了数值的大小。
而这道题目没有限制数值的大小,就无法使用数组来做哈希表了。
而且如果哈希值比较少、特别分散、跨度非常大,使用数组就造成空间的极大浪费。所以我们打算选择set。
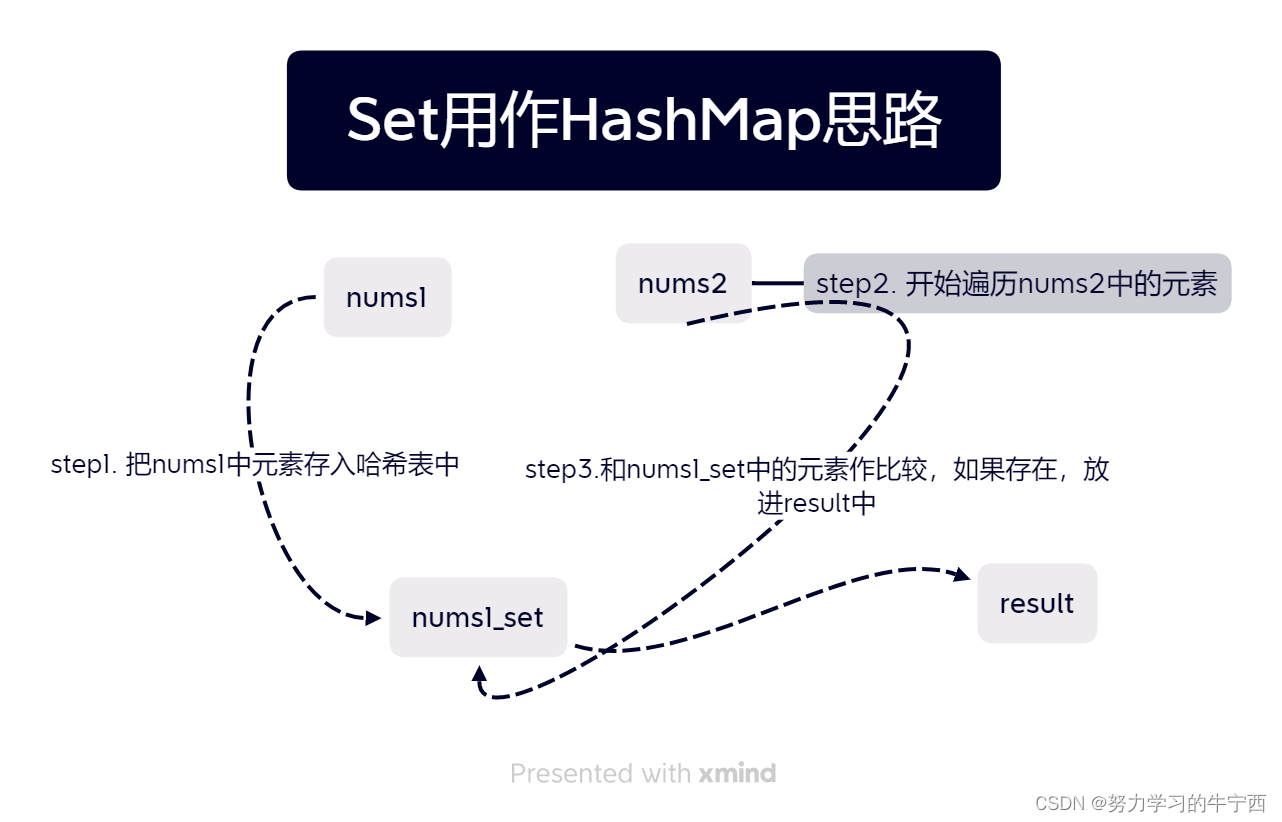
用set的思路如下:
- 首先,定义一个set哈希表,称为result,存放之后要返回的结果,之所以用set是因为它可以在insert元素的时候就自动去重;
- 把nums1中的元素放进另一个set哈希表中(会做去重操作),定义为num1_set;
- 遍历nums2中的元素,然后再nums1_set这个哈希表中找有没有出现,如果找到了的话,就把它存到result中去;
- 遍历结束之后,将result转换为list返回
2. 代码实现
# 把set用作hashMap
# time:O(N);space:O(N)
class Solution(object):
def intersection(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: List[int]
"""
# 保存结果的result初始化
result = set()
# 将nums1中的元素存入set中
nums1_set = set(nums1)
# 遍历nums2,和nums1_set比较,如果存在,就加进result
for item in nums2:
if item in nums1_set:
result.add(item)
return list(result)3. 复杂度分析
时间复杂度和空间复杂度都是O(N)。
将nums1中的元素存入set数据结构中,就是O(N)的时间复杂度,然后遍历num2中的元素一个个比较,又是O(N)的时间复杂度,最后把result转换成list,也是O(N)的时间复杂度,所以总体来说time complexity = O(N);空间上创建了两个set和一个list,长度都是O(N)数量级的,所以space complexity = O(N)。
4. 思考
(1)以上方法实际上是一个各种语言通用的思路,下面讲讲在Python和C++中这种方法应用的一些特殊的注意点
(2)在Python中实际上可以写的非常简单
可以直接把两个数组,变成两个集合(去除重复),然后取两个集合的交集,再把这个交集变为数组返回即可,所以Python一句话就解决了;
代码实现
class Solution(object):
def intersection(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: List[int]
"""
# Approach 1
# complexity analysis time O(N) space O(N)
return list(set(nums1)&set(nums2))这里可以复习一波Python关于set的知识点
- 描述:set() 函数创建一个无序不重复元素集,可进行关系测试,删除重复数据,还可以计算交集、差集、并集等;
- set 语法:
class set([iterable])参数说明:iterable -- 可迭代对象对象; - 返回值:返回新的集合对象;
- 以下实例展示了 set 的使用方法:
>>>x = set('runoob')
>>> y = set('google')
>>> x, y
(set(['b', 'r', 'u', 'o', 'n']), set(['e', 'o', 'g', 'l']))
# 重复的被删除
>>> x & y # 交集
set(['o'])
>>> x | y # 并集
set(['b', 'e', 'g', 'l', 'o', 'n', 'r', 'u'])
>>> x - y # 差集
set(['r', 'b', 'u', 'n'])
>>>5. Python集合Set添加元素
添加元素有两种方式,分别为:使用 add 方法和使用 update 方法。
add 方法将需要添加的元素当做一个整体,添加到集合中去,而 update 方法是把要传入的元素拆分,做为个体传入到集合中。使用 add 添加集合元素语法:s.add('python');使用 update 添加集合元素语法:s.update('python')。
# 使用 add 添加元素集合
# 我们使用 {} 定义了一个集合 s,集合的第一个和第二个元素都是 string 类型
# 第三个元素是 int 类型的。接着,我们使用 add 方法,
# 给集合 s 添加一个元素 Python, 最后,我们使用 print 打印集合的内容。
>>> s = {"Hello", "HaiCoder", 1024}
>>> s.add("Python")
>>> print("Set =", s)
Set = {'Hello', 1024, 'Python', 'HaiCoder'}
>>>
# 使用 add 添加元素集合
# 我们使用 {} 定义了一个集合 s,使用 () 定义了一个 元祖 tup,
# 接着,使用集合的 add 方法将元祖 tup 添加到集合 s 中。
# 最后,我们使用 print 打印集合内容,
# 发现,整个元祖被当做了一个元素添加到了集合中
>>> s = {"Hello", "HaiCoder", 1024}
>>> tup = ("Python", "Golang", "JavaScript")
>>> s.add(tup)
>>> print("Set =", s)
Set = {'Hello', 1024, 'HaiCoder', ('Python', 'Golang', 'JavaScript')}
# 使用 update 添加元素集合
# 我们使用 {} 定义了一个集合 s,接着,我们使用 update 方法,
# 给集合 s 添加一个元素 Python, 最后,我们使用 print 打印集合的内容。
# 我们发现,字符串 Python 被拆分为了一个个字符,作为一个单独元素添加到了集合中去。
>>> s = {"Hello", "HaiCoder", 1024}
>>> s.update("Python")
>>> print("Set =", s)
Set = {'Hello', 1024, 'h', 'HaiCoder', 'n', 'P', 'o', 'y', 't'}
# 使用 update 添加元素集合
# 我们使用 {} 定义了一个集合 s,使用 () 定义了一个元素 tup,
# 接着,使用集合的 update 方法将元祖 tup 添加到集合 s 中。
# 最后,我们使用 print 打印集合内容,发现,
# 元组的每一个元素都被拆分为了一个个单独的元素添加到了集合中。
>>> s = {"Hello", "HaiCoder", 1024}
>>> tup = ("Python", "Golang", "JavaScript")
>>> s.update(tup)
>>> print("Set =", s)
Set = {'Hello', 1024, 'HaiCoder', 'JavaScript', 'Python', 'Golang'}6. Python中从集合删除元素
Python 中的 set.remove() 函数与集合一起使用以从调用集合中删除特定元素。remove()函数将要删除的元素作为参数,并从调用集中删除指定的元素。如果在调用集合中找不到该元素,remove()函数会引发 KeyError异常。请参考以下代码示例。
set1 = {1,2,3,4,5,6,7,8,9,0}
set1.remove(5)
print(set1)
#output
{0, 1, 2, 3, 4, 6, 7, 8, 9}discard() 函数与 remove()函数非常相似。它还可用于仅从 Python 中的集合中删除单个元素。discard()函数将要删除的元素作为输入参数,如果该值存在于该特定集合中,则将其从调用集合中删除。唯一的区别是,如果调用集中不存在该值,则 discard() 函数不会引发 KeyError。
set1 = {1,2,3,4,5,6,7,8,9,0}
set1.discard(51)
print(set1)
# output
{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}我们可以使用 -运算符在 Python 中执行集差操作。-运算符从左集合中删除右集合的所有元素,并以另一个集合的形式返回结果。如果左集合的元素不存在于右集合中,则此方法不会引发任何异常,并返回右集合作为其结果。以下代码片段向我们展示了如何使用 -运算符从集合中删除多个元素。
set1 = {1,3,5,7,9}
set2 = {2,4,6,8,0}
set1 = set1 - set2
print(set1)
#output
{1, 3, 5, 7, 9}注意:还有difference和difference_update可以参见reference3
(3) 在C++中实现需要注意的事项:
关于C++ 各种set的选择;关于set,C++ 给提供了如下三种可用的数据结构:
- std::set
- std::multiset
- std::unordered_set
std::set和std::multiset底层实现都是红黑树,std::unordered_set的底层实现是哈希表, 使用unordered_set 读写效率是最高的,并不需要对数据进行排序,而且还不要让数据重复,所以选择unordered_set。

class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result_set; // 存放结果
unordered_set<int> nums_set(nums1.begin(), nums1.end());
for (int num : nums2) {
// 发现nums2的元素 在nums_set里又出现过
if (nums_set.find(num) != nums_set.end()) {
result_set.insert(num);
}
}
return vector<int>(result_set.begin(), result_set.end());
}
};(4) 疑问:遇到哈希问题我直接都用set不就得了,用什么数组啊!
直接使用set 不仅占用空间比数组大,而且速度要比数组慢,set把数值映射到key上都要做hash计算的。不要小瞧 这个耗时,在数据量大的情况,差距是很明显的。
方法二:用数组作HashMap
1. 思路
因为LeetCode给了限制
1 <= nums1.length, nums2.length <= 10000 <= nums1[i], nums2[i] <= 1000
所以说这道题也可以使用数组作哈希表实现。
思路如下:
- 创建一个result set, 创建一个默认数值全为0的数组,大小只要比1000大一点点就可以了;
- 数组的下标索引就表示数值,数组中的值如果是1,表示出现过,如果为0,表示没出现过;
- 遍历nums1,将数值作为数组的索引,赋值对应位置为1,如果重复出现该数值,该位置会重复覆盖1这个值,并不影响;
- 然后遍历nums2,同时看对应在数组中的值是否为1,如果为1,证明是两个数组的交集元素,加入result中
- 遍历结束后,result集合转为list输出。
2. 代码实现
# 数组作hashMap
# time:O(N); space:O(N)
class Solution(object):
def intersection(self, nums1, nums2):
"""
:type nums1: List[int]
:type nums2: List[int]
:rtype: List[int]
"""
# 初始化存放交集的集合,可以自动去重
result = set()
# 初始化hashMap,因为LeetCode中限制了集合中元素的大小<=1000
# 所以初始化一个稍大于1000的数组就可以了
record = [0]*1002
# 遍历nums1,把数值的大小作为索引下标,对应的元素为0或1
# 如果出现了,把对应的下标值赋值为1
for item in nums1:
record[item] = 1
# 遍历nums2,看看在数组中对应是否在nums1中出现过
# 如果出现过的话说明是交集元素,放入result中
for item in nums2:
if record[item] == 1:
result.add(item)
return list(result)3. 复杂度分析
时间复杂度和空间复杂度均为O(N);
在时间上,因为需要分别遍历nums1和nums2,均为O(N),所以整体复杂度为O(N);
在空间上,因为需要新建一个result的set,为O(N),因为nums1和2 最大的长度限制在1000以内,所以新建的数组不能认为是常数级别了(not sure),新建的数组,空间复杂度也为O(N),整体空间复杂度为O(N)。
4. 思考
eetcode加上限制条件之后,实际上用数组解决这道题目的效率是更高的,因为set每往里insert一个值,他会对你这个值作哈希运算,转变成另一个它内部储存的值,同时还要去开辟一个新的空间,这些操作都是要花一些时间的,而数组直接用下标来作哈希映射,这种方式是最快的。
本题学习时间:120分钟。
Reference
2. Python 集合(set)添加元素-Python 集合(set) add-Python 集合(set) update-嗨客网
3. 在 Python 中从集合中删除元素 | D栈 - Delft Stack
Leetcode202.快乐数
方法: Set用作HashMap
1. 思路
我们可以先举几个例子。我们从 7开始。则下一个数字是 49因为 7^2=49),然后下一个数字是 97(4^2+9^2=97)。我们可以不断重复该的过程,直到我们得到 1。因为我们得到了 1,我们知道 7 是一个快乐数,函数应该返回 true。

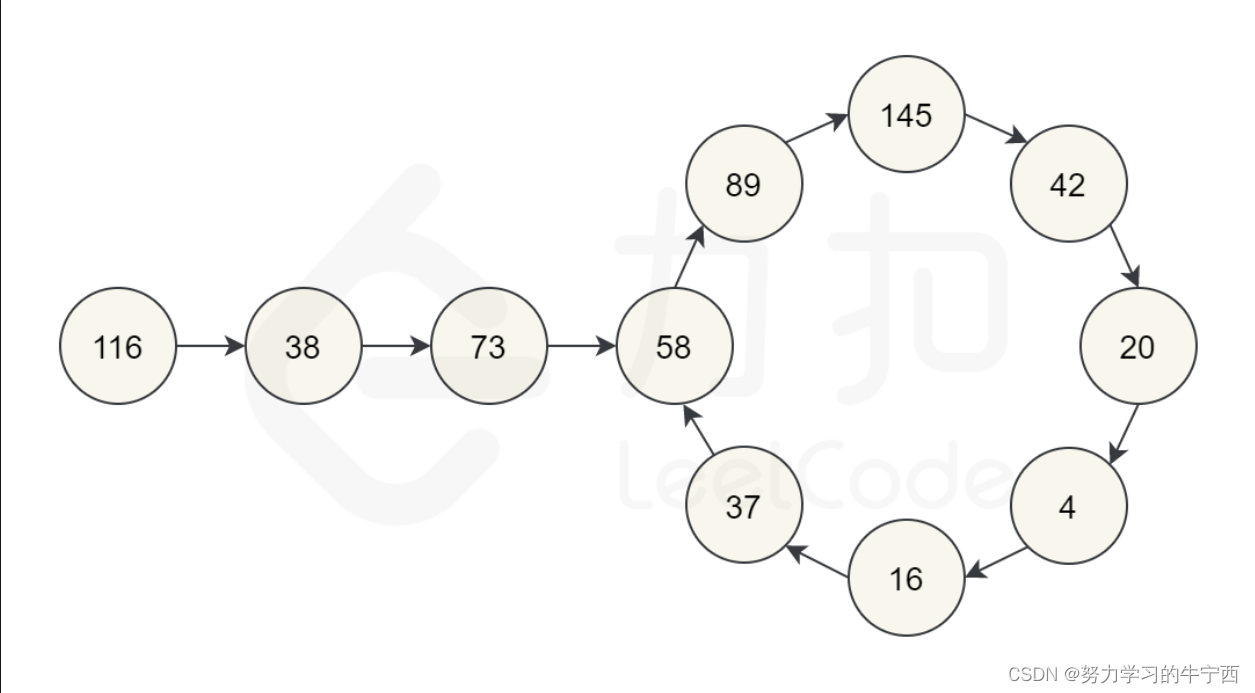
再举一个例子,让我们从 116开始。通过反复通过平方和计算下一个数字,我们最终得到 58,再继续计算之后,我们又回到 58。由于我们回到了一个已经计算过的数字,可以知道有一个循环,因此不可能达到 1。所以对于 116,函数应该返回 false。
根据我们的探索,我们猜测会有以下三种可能。
- 最终会得到 1。
- 最终会进入循环。
- 值会越来越大,最后接近无穷大。
第三个情况比较难以检测和处理。我们怎么知道它会继续变大,而不是最终得到 11 呢?我们可以仔细想一想,每一位数的最大数字的下一位数是多少。
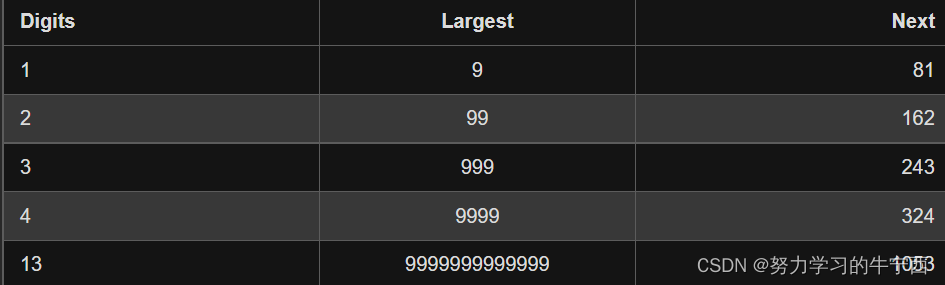
3 位数的数字,它不可能大于 243。这意味着它要么被困在 243 以下的循环内,要么跌到 1。
对于这个结论可以这样理解:就算它算243次,把所有243个数全部占了一遍,那在算244次的时候,是不是一定会重复。所以说3位数及以下的数,要么被困在243以下的循环里,要么跌到1。
4位或 4位以上的数字在每一步都会丢失一位,直到降到 3位为止。
LeetCode给的限制条件是1 <= n <= 2^31 - 1
2^31 = 2,147,483,648 (10位数) 最大也就999 999 999 9,next是810,也是三位数。
所以我们知道,最坏的情况下,算法可能会在 243 以下的所有数字上循环,然后回到它已经到过的一个循环或者回到 1。但它不会无限期地进行下去,所以我们排除第三种选择。
即使在代码中你不需要处理第三种情况,你仍然需要理解为什么它永远不会发生,这样你就可以证明为什么你不处理它。
这道题目看上去貌似一道数学问题,其实并不是!题目中说了会 无限循环,那么也就是说求和的过程中,如果是不满足快乐数的条件,sum会重复出现,这对解题很重要!
当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法了。
所以这道题目使用哈希法,来判断这个sum是否重复出现,如果重复了就是return false, 否则一直找到sum为1为止。
确定了用哈希表之后,思考,用哪种数据结构,这道题没有key-value的键值对,元素个数不确定,决定用set来实现。
2. 代码实现
# 方法:set用作哈希表
# complexity analysis
# time:O(logN);space:O(logN)
class Solution(object):
def isHappy(self, n):
"""
:type n: int
:rtype: bool
"""
# 计算拆分的平方和的子函数
def squareSum(number):
square_sum = 0
while number:
square_sum += (number%10) ** 2
number = number//10
return square_sum
record = set()
while True:
n = squareSum(n) # 这里不能定义一个新的变量,要把原来的n覆盖
if n == 1:
return True
elif n in record:
return False
else:
record.add(n)3. 复杂度分析
时间复杂度:O(243 * 3 + log n + log log n + log log log n). = O(logn)。
- 查找给定数字的下一个值的成本为 O(log n),因为我们正在处理数字中的每位数字,而数字中的位数由log n 给定;
- 要计算出总的时间复杂度,我们需要仔细考虑循环中有多少个数字,它们有多大;
- 我们在上面确定,一旦一个数字低于243,它就不可能回到 243 以上。因此,我们就可以用 243 以下最长循环的长度来代替 243,不过,因为常数无论如何都无关紧要,所以我们不会担心它;
- 对于高于 243 的 n,我们需要考虑循环中每个数高于 243 的成本。通过数学运算,我们可以证明在最坏的情况下,这些成本将是 O(log n) + O(log log n) + O( log log log n)...幸运的是,O(log n)是占主导地位的部分,而其他部分相比之下都很小(总的来说,它们的总和小于logn),所以我们可以忽略它们。
空间复杂度:O(logn)。
与空间复杂度密切相关的是衡量我们放入哈希集合中的数字以及它们有多大的指标。对于足够大的n,大部分空间将由 n 本身占用。放入哈希集合中的下一个元素的大小应该是logn量级的。(? not sure)
另外提一句,我们可以很容易地把空间复杂度优化到 O(243 * 3) = O(1),方法是只保存集合中小于 243 的数字,因为对于较高的数字,无论如何都不可能返回到它们。
4. 思考
(1)一个难点是求和的过程,对取数值各个位上的单数操作要熟悉;
def squareSum(number):
square_sum = 0
while number:
square_sum += (number%10) ** 2
number = number//10
return square_sum(2) 看上去毫无头绪的题目,要通过举各种情况的例子来找思路;
(3)本题的复杂度分析有点难。
本题学习时间:75分钟。
Reference
1. 力扣
2. 代码随想录
Leetcode1. 两数之和
方法: Map作哈希表
1. 思路
很明显暴力的解法是两层for循环查找,时间复杂度是O(n^2),,不再赘述。
为什么想到用哈希法?
当我们需要查询一个元素是否出现过,或者一个元素是否在集合里的时候,就要第一时间想到哈希法。
本题呢,我就需要一个集合来存放我们遍历过的元素,然后在遍历数组的时候去询问这个集合,某元素是否遍历过,也就是 是否出现在这个集合。
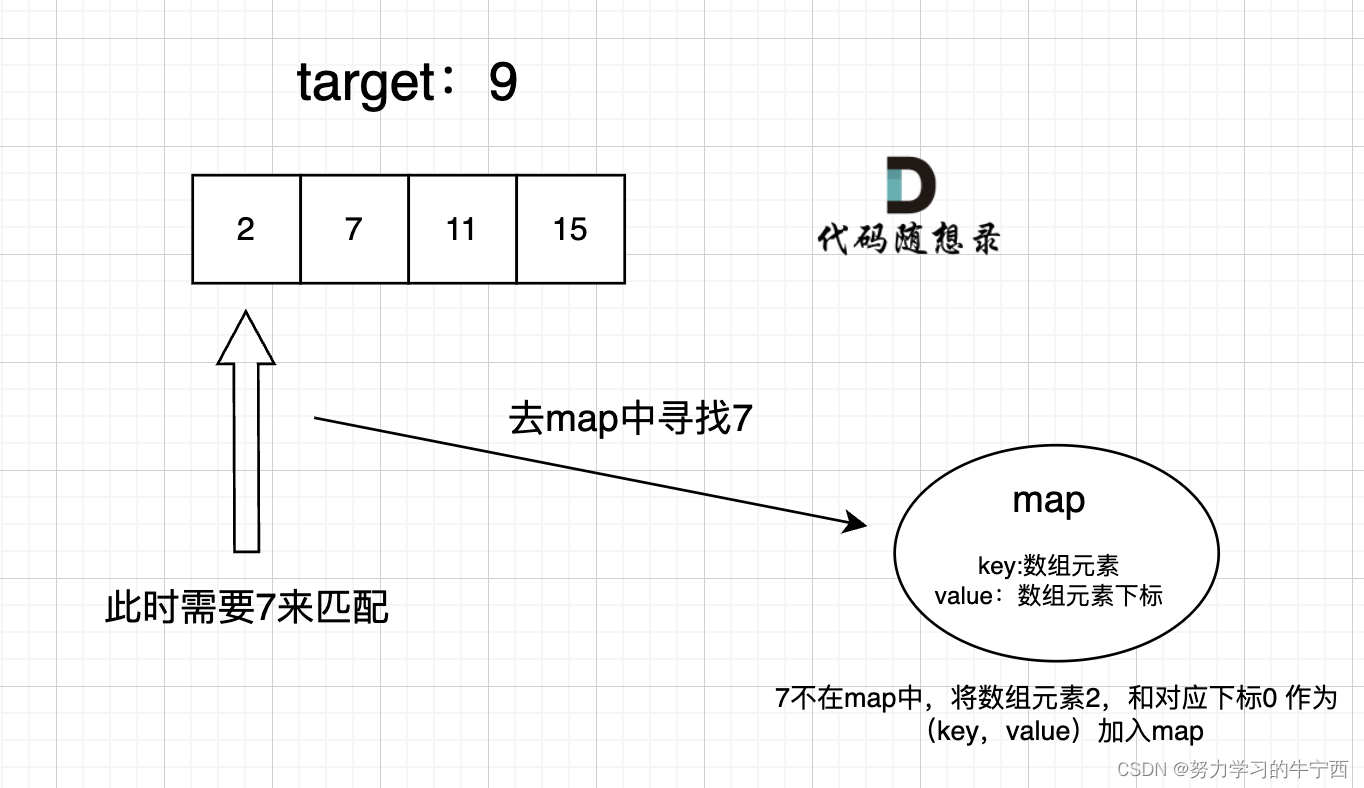
例如遍历到第二个数,7的时候,我们需要查target-7=2,是否出现过。
那么我们就应该想到使用哈希法了。
用什么数据结构当做哈希表?
因为本地,我们不仅要知道元素有没有遍历过,还有知道这个元素对应的下标,需要使用 key value结构来存放,key来存元素,value来存下标,那么使用map正合适。
再来看一下使用数组和set来做哈希法的局限。
- 数组的大小是受限制的,而且如果元素很少,而哈希值太大会造成内存空间的浪费。
- set是一个集合,里面放的元素只能是一个key,而两数之和这道题目,不仅要判断y是否存在而且还要记录y的下标位置,因为要返回x 和 y的下标。所以set 也不能用。
此时就要选择另一种数据结构:map ,map是一种key value的存储结构,可以用key保存数值,用value在保存数值所在的下标。
Map 用来做什么?
map目的用来存放我们访问过的元素,因为遍历数组的时候,需要记录我们之前遍历过哪些元素和对应的下表,这样才能找到与当前元素相匹配的(也就是相加等于target)
Map中key和value分别表示什么?
这道题 我们需要 给出一个元素,判断这个元素是否出现过,如果出现过,返回这个元素的下标。
那么判断元素是否出现,这个元素就要作为key,所以数组中的元素作为key,有key对应的就是value,value用来存下标。
所以 map中的存储结构为 {key:数据元素,value:数组元素对应的下表}。
在遍历数组的时候,只需要向map去查询是否有和目前遍历元素比配的数值,如果有,就找到的匹配对,如果没有,就把目前遍历的元素放进map中,因为map存放的就是我们访问过的元素。
实现过程叙述
从左到右遍历,数组中的数字,每次处理方式是这样,算出target-value在不在dictionary中,如果不在,把key = 当前遍历位置的数值;value= 当前遍历位置的索引,加到字典中去,然后下一个。
如果算出target- value在dictionary中,那么返回字典记录的索引和当前的索引值。

2. 代码实现
# time:O(N);space:O(N)
class Solution(object):
def twoSum(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: List[int]
"""
record = {}
for index,value in enumerate (nums):
if (target-value) not in record:
record[value] = index
else:
return [record[target-value],index]
return []3. 复杂度分析
时间复杂度:O(N)
因为nums中的每个值都要遍历一遍做相应的处理,所以为O(N);
空间复杂度:O(N)
因为要创建一个字典数据结构,然后储存遍历过数据的信息,空间复杂度为O(N)
4. 思考
(1)本题其实有四个重点:
- 为什么会想到用哈希表
- 哈希表为什么用map
- 本题map是用来存什么的
- map中的key和value用来存什么的
把这四点想清楚了,本题才算是理解透彻了。
(2)C++ 实现的特殊注意点
C++中map,有三种类型:
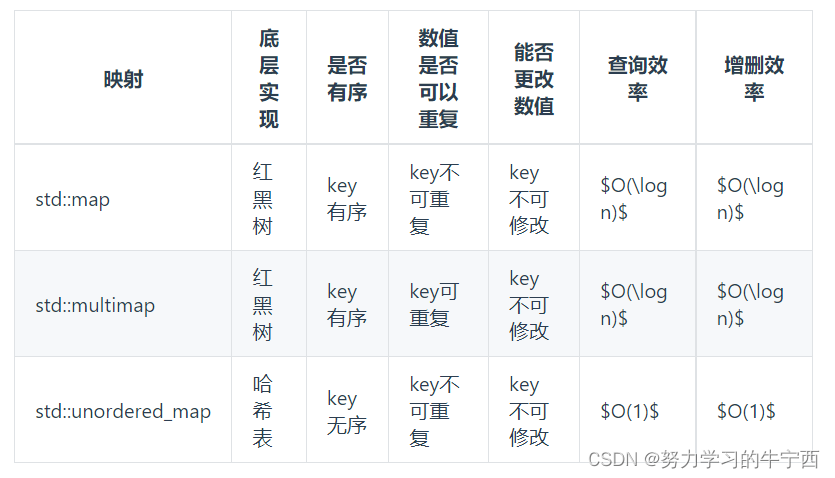
std::unordered_map 底层实现为哈希表,std::map 和std::multimap 的底层实现是红黑树。
同理,std::map 和std::multimap 的key也是有序的(这个问题也经常作为面试题,考察对语言容器底层的理解)。
这道题目中并不需要key有序,选择std::unordered_map 效率更高!
代码实现
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
std::unordered_map <int,int> map;
for(int i = 0; i < nums.size(); i++) {
auto iter = map.find(target - nums[i]);
if(iter != map.end()) {
return {iter->second, i};
}
map.insert(pair<int, int>(nums[i], i));
}
return {};
}
};Reference:
本题学习时间: 40分钟。
今日算法刷题时间:5小时。
ps: 今天四道题的总结写了一万多字 ,按照思路,代码,复杂度,思考四个部分,写的超详细,补充了很多相关的知识点(求推荐!感谢嘻嘻)