题目描述
小明对于喝水这件事很执着,每次要和n杯水,但要求每个杯子里水的温度都相同,请问这可能吗?
小明有一个大水缸,里面水的温度为T单位,体积为C升。另有n杯水(假设每个杯子的容量是无限的),每杯水的温度为t[i]单位,体积为c[i]升。
小明现在要把大水缸的水倒入n杯水中,使得n杯水的温度相同,请问这可能吗?并求出可行的最高温度,保留4位小数。
注意:一杯温度为t1单位、体积为c1升的水与另一杯温度为t2单位、体积为c2升的水混合后,温度变为(t1*c1+t2*c2)/(c1+c2),体积变为c1+c2。
输入
第一行一个整数n, 1 ≤ n ≤ 10^5
第二行两个整数T,C,其中0 ≤ T ≤ 10^4, 0 ≤ C ≤ 10^9
接下来n行每行两个整数t[i],c[i]
0 < t[i], c[i] ≤ 10^4
输出
如果不行,输出“Impossible”(不带引号)否则第一行输出“Possible"(不带引号),第二行输出一个保留4位小数的实数表示答案。、
样例解释:往第二杯水中倒0.5升水
往第三杯水中到1升水
三杯水的温度都变成了20
样例输入 Copy
3
10 2
20 1
25 1
30 1
样例输出 Copy
Possible
20.0000
个人理解:一道数学和算法的结合题,数学上要考验转换公式的,算法是还要考虑如果大水缸里面的温度比all水杯的温度还要高的话,看看还能不能更高,这里用到了二分并查集,也是非常容易忽略的一点。
二分并查集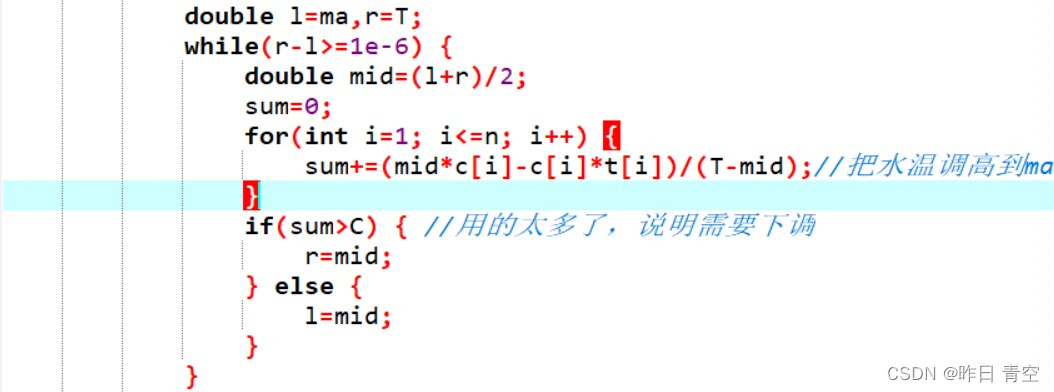
最小值为all水杯最高温度,最大值为水缸里面的温度,进行二分
数学题就是温度公式转换成水的体积公式
代码如下:
#include<bits×dc++.h>
using namespace std;
const int N=1e5+5;
int n;
double t[N],c[N];
double T,C;
int main() {
cin>>n;
double mi=1.0*(0x3f),ma=-1;
//记录水的最大温度和最小温度
cin>>T>>C;
for(int i=1; i<=n; i++) {
scanf("%lf %lf",&t[i],&c[i]);
mi=min(mi,t[i]);
ma=max(ma,t[i]);
}
if((mi<T&&ma>=T)||(mi<=T&&ma>T))
//如果水的温度在最小和最大之间并且最小和最大并不相等
{
cout<<"Impossible\n";
return 0;
}
double sum=0;//记录需要的总水量
if(mi>=T) {//最小值大于T
//那么尝试将所有水都调至最小温度
for(int i=1; i<=n; i++) {
sum+=(mi*c[i]-c[i]*t[i])/(T-mi);
//根据公式推导出将温度调制mi需要的水
}
if(sum>C)cout<<"Impossible\n";
else printf("Possible\n%.4lf\n",mi);
}
else if(ma<=T) { //最大值小于T
for(int i=1; i<=n; i++) {
sum+=(ma*c[i]-c[i]*t[i])/(T-ma);//把水温调高到ma
}
if(sum>C)cout<<"Impossible\n";
else {
//试试还能不能调搞
double l=ma,r=T;
while(r-l>=1e-6) {
double mid=(l+r)/2;
sum=0;
for(int i=1; i<=n; i++) {
sum+=(mid*c[i]-c[i]*t[i])/(T-mid);//把水温调高到ma
}
if(sum>C) { //用的太多了,说明需要下调
r=mid;
} else {
l=mid;
}
}
printf("Possible\n%.4lf\n",l);
}
}
return 0;
}