神经网络与深度学习-作业1

发布于：2022-12-13 ⋅ 阅读:(545) ⋅ 点赞:(0)

习题 2-1 分析为什么平方损失函数不适用于分类问题 , 交叉熵损失函数不适用于回归问题？

解：交叉熵损失的假设是误差分布是二值分布，因此更适用于分类等离散属性的问题，而均方误差则假设数据的分布是正态分布，更加是用于连续属性的误差分析。

习题 2-12 对于一个三分类问题，数据集的真实标签和模型的预测标签如下：

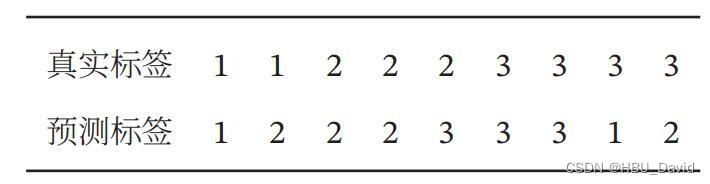
分别计算模型的精确率、召回率、F1值以及它们的宏平均和微平均．

格式要求：使用公式编辑器，在博客上正确书写公式。

解：

精确率： $\frac{TP}{TP+FP}$

分类1的精确率： $\frac{1}{2}$

分类2的精确率： $\frac{2}{4}=\frac{1}{2}$

分类3的精确率： $\frac{2}{3}$

召回率： $\frac{TP}{TP+FN}$

分类1的召回率： $\frac{1}{2}$

分类2的召回率： $\frac{2}{3}$

分类3的召回率： $\frac{2}{4} = \frac{1}{2}$

F1值： $\frac{precision\cdot recall}{precision\dotplus recall }\cdot 2$

分类1的F1值： $\frac{\frac{1}{2}\cdot \frac{1}{2}}{\frac{1}{2}\dotplus \frac{1}{2}}\cdot 2=\frac{1}{2}$

分类2的F1值： $\frac{\frac{1}{2}\cdot \frac{2}{3}}{\frac{1}{2}\dotplus \frac{2}{3}}\cdot 2 = \frac{4}{7}$

分类3的F1值： $\frac{\frac{2}{3}\cdot \frac{1}{2}}{\frac{2}{3}\dotplus \frac{1}{2}}\cdot 2=\frac{4}{7}$

宏平均： $\frac{1}{n}\sum_{i=1}^{n}P_{i}$

宏查准率： $P1 = \frac{1}{3}\ast (\frac{1}{2}\dotplus \frac{1}{2}\dotplus \frac{2}{3})=\frac{5}{9}$

宏查全率： $P2 = \frac{1}{3}\ast (\frac{1}{2}\dotplus \frac{2}{3}\dotplus \frac{1}{2})=\frac{5}{9}$

F1: $F1 = 2\ast \frac{\frac{5}{9}\cdot \frac{5}{9}}{\frac{5}{9}\dotplus \frac{5}{9}}=\frac{5}{9}$

微平均：

$P_{micro} = \frac{\sum_{i=1}^{n}TP_{i}}{\sum_{i=1}^{n}TP_{i}\dotplus \sum_{i=1}^{n}FP_{i}} = \frac{1+2+2}{(1+2+1)+(1+2+2))}=\frac{5}{9}$

$R_{micro} = \frac{\sum_{i=1}^{n}TR_{i}}{\sum_{i=1}^{n}TR_{i}+\sum_{i=1}^{n}FN_{i}}=\frac{1+2+2}{(1+2+2)+(1+1+2)} = \frac{5}{9}$

$F1_{micro} = 2\ast \frac{P_{micro}\ast R_{micro}}{P_{micro} + R_{micro}}=\frac{5}{9}$

本文含有隐藏内容，请开通VIP 后查看