机器学习笔记之隐马尔可夫模型——后向算法处理求值问题
引言
上一节介绍了基于隐马尔可夫模型使用前向算法处理求值问题,本节将介绍另一种求值问题方法——后向算法(Backward Algorithm)。
回顾:前向算法
关于隐马尔可夫模型的基础概念、模型参数相关的数学符号表示见机器学习笔记之隐马尔可夫模型(二)背景介绍一节。
求值问题
求值问题(Evaluation)本质上是在给定隐马尔可夫模型参数 λ \lambda λ的条件下,求解观测序列 O = { o 1 , o 2 , ⋯ , o T } \mathcal O = \{o_1,o_2,\cdots,o_T\} O={o1,o2,⋯,oT}发生的概率大小 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)。
前向算法
前向算法(Forward Algorithm)的逻辑如下图所示。
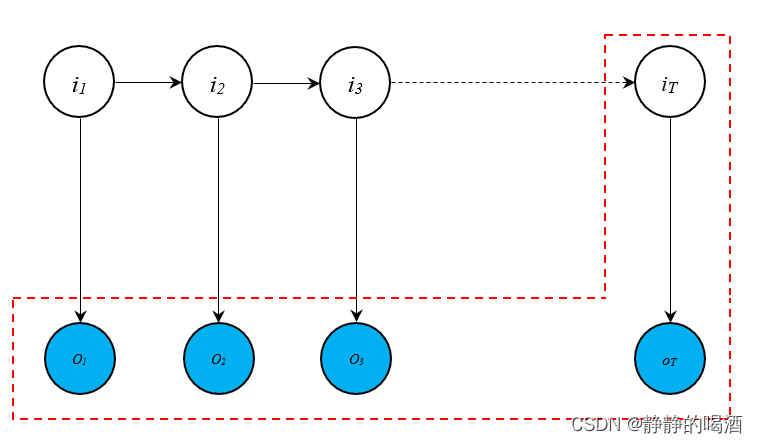
其核心思想是当前 t t t时刻状态变量 i t = q i i_t=q_i it=qi的条件下, i t i_t it与初始时刻到当前时刻的观测变量 { o 1 , ⋯ , o t } \{o_1,\cdots,o_t\} {o1,⋯,ot}的联合概率分布 P ( o 1 , ⋯ , o t , i t = q i ∣ λ ) P(o_1,\cdots,o_t,i_t=q_i \mid \lambda) P(o1,⋯,ot,it=qi∣λ)与 t + 1 t+1 t+1时刻的联合概率分布 P ( o 1 , ⋯ , o t , o t + 1 , i t + 1 = q j ∣ λ ) P(o_1,\cdots,o_t,o_{t+1},i_{t+1}=q_j \mid \lambda) P(o1,⋯,ot,ot+1,it+1=qj∣λ)之间的关联关系。
基于齐次马尔可夫假设与观测独立性假设,记:
α t ( i ) = P ( o 1 , ⋯ , o t , i t = q i ∣ λ ) α t + 1 ( j ) = P ( o 1 , ⋯ , o t , o t + 1 , i t + 1 = q j ∣ λ ) \alpha_{t}(i) = P(o_1,\cdots,o_t,i_t=q_i \mid \lambda) \\ \alpha_{t+1}(j) = P(o_1,\cdots,o_t,o_{t+1},i_{t+1}=q_j \mid \lambda) αt(i)=P(o1,⋯,ot,it=qi∣λ)αt+1(j)=P(o1,⋯,ot,ot+1,it+1=qj∣λ)
α t ( i ) \alpha_{t}(i) αt(i)与 α t + 1 ( j ) \alpha_{t+1}(j) αt+1(j)之间关联关系表示如下:
α t + 1 ( j ) = ∑ i = 1 K [ P ( o t + 1 ∣ i t + 1 = q j ) ⋅ P ( i t + 1 = q j ∣ i t = q i , λ ) ⋅ α t ( i ) ] \begin{aligned} \alpha_{t+1}(j) = \sum_{i=1}^{\mathcal K}[P(o_{t+1} \mid i_{t+1} = q_j) \cdot P(i_{t+1} = q_j \mid i_t = q_i,\lambda) \cdot \alpha_t(i)] \end{aligned} αt+1(j)=i=1∑K[P(ot+1∣it+1=qj)⋅P(it+1=qj∣it=qi,λ)⋅αt(i)]
至此,从 α 0 ( i ) \alpha_0(i) α0(i)开始,执行 T T T次迭代,得到最终结果 α T ( i ) \alpha_{T}(i) αT(i)。最终对 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)进行求解:
P ( O ∣ λ ) = ∑ i = 1 K α T ( i ) P(\mathcal O \mid \lambda) = \sum_{i=1}^{\mathcal K} \alpha_{T}(i) P(O∣λ)=i=1∑KαT(i)
因此, P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)的时间复杂度为 O ( K 2 × T ) O(\mathcal K^2 \times \mathcal T) O(K2×T)。
后向算法
整体逻辑
后向算法的逻辑如下图所示(蓝色部分):
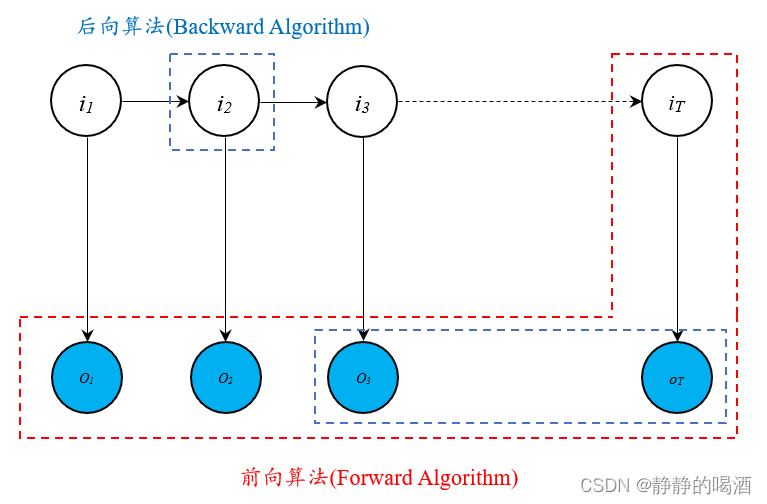
后向算法的核心思想共包含两项:
给定隐马尔可夫模型的参数 λ \lambda λ条件下, t + 1 t+1 t+1时刻到最终时刻的观测变量 { o t + 1 , ⋯ , o T } \{o_{t+1},\cdots,o_{T}\} {ot+1,⋯,oT}关于 t t t时刻状态变量 i t = q i i_t = q_i it=qi的条件概率分布 P ( o t + 1 , ⋯ , o T ∣ i t = q i , λ ) P(o_{t+1},\cdots,o_{T} \mid i_t = q_i,\lambda) P(ot+1,⋯,oT∣it=qi,λ)与 t t t时刻的条件概率分布 P ( o t , ⋯ , o T ∣ i t − 1 , λ ) P(o_t,\cdots,o_T \mid i_{t-1},\lambda) P(ot,⋯,oT∣it−1,λ)之间的关联关系。数学符号表达如下:
β t ( i ) = P ( o t + 1 , ⋯ , o T ∣ i t = q i , λ ) β t − 1 ( i ) = P ( o t , ⋯ , o T ∣ i t − 1 = q j , λ ) β t ( i ) ↔ ? β t − 1 ( i ) \beta_t(i) =P(o_{t+1},\cdots,o_{T} \mid i_t = q_i,\lambda) \\ \beta_{t-1}(i) = P(o_{t},\cdots,o_{T} \mid i_{t-1} = q_j,\lambda) \\ \beta_t(i) \overset{\text{?}}{\leftrightarrow}\beta_{t-1}(i) βt(i)=P(ot+1,⋯,oT∣it=qi,λ)βt−1(i)=P(ot,⋯,oT∣it−1=qj,λ)βt(i)↔?βt−1(i)该算法的迭代方式是 从后向前迭代。即初始状态是 β T ( i ) \beta_T(i) βT(i):
β T ( i ) = P ( i T = q i , λ ) \beta_{T}(i) = P(i_T = q_i,\lambda) βT(i)=P(iT=qi,λ)
通过 T T T次迭代,得到迭代的尽头 β 1 ( i ) \beta_{1}(i) β1(i):
β 1 ( i ) = P ( o 2 , ⋯ , o T ∣ i 1 = q i , λ ) \beta_1(i) = P(o_2,\cdots,o_T \mid i_1 = q_i,\lambda) β1(i)=P(o2,⋯,oT∣i1=qi,λ)
只要找出 β 1 ( i ) \beta_1(i) β1(i)和 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)之间的关联关系,即可通过 β 1 ( i ) \beta_1(i) β1(i)求解 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ):
β 1 ( i ) ↔ ? P ( O ∣ λ ) \beta_1(i)\overset{\text{?}}{\leftrightarrow}P(\mathcal O \mid \lambda) β1(i)↔?P(O∣λ)
β 1 ( i ) \beta_1(i) β1(i)和 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)之间的关联关系
观察:最终迭代求解的 β 1 ( i ) \beta_1(i) β1(i)和 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)有什么联系:
- 将 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)展开:
P ( O ∣ λ ) = P ( o 1 , o 2 , ⋯ , o T ∣ λ ) P(\mathcal O \mid \lambda) = P(o_1,o_2,\cdots,o_T \mid \lambda) P(O∣λ)=P(o1,o2,⋯,oT∣λ) - 使用条件概率密度积分将状态变量 i 1 = q i i_1 = q_i i1=qi引进来:
i 1 i_1 i1是状态变量,存在K \mathcal K K种选择。
P ( O ∣ λ ) = ∑ i 1 P ( o 1 , ⋯ , o T , i 1 = q i , λ ) = ∑ i = 1 K P ( o 1 , ⋯ , o T , i 1 = q i , λ ) = ∑ i = 1 K [ P ( o 1 , ⋯ , o T ∣ i 1 = q i , λ ) ⋅ P ( i 1 = q i , λ ) ] \begin{aligned} P(\mathcal O \mid \lambda) & = \sum_{i_1} P(o_1,\cdots,o_T,i_1 = q_i,\lambda) \\ & = \sum_{i=1}^{\mathcal K} P(o_1,\cdots,o_T,i_1 = q_i,\lambda) \\ & = \sum_{i=1}^{\mathcal K} \left[P(o_1,\cdots,o_T \mid i_1 = q_i,\lambda)\cdot P(i_1 = q_i,\lambda)\right] \end{aligned} P(O∣λ)=i1∑P(o1,⋯,oT,i1=qi,λ)=i=1∑KP(o1,⋯,oT,i1=qi,λ)=i=1∑K[P(o1,⋯,oT∣i1=qi,λ)⋅P(i1=qi,λ)]
观察 P ( i 1 = q i , λ ) P(i_1 = q_i,\lambda) P(i1=qi,λ),它是模型参数 λ \lambda λ中的初始概率分布 π \pi π,因此,上式可转化如下:
P ( O ∣ λ ) = ∑ i = 1 K [ P ( o 1 , ⋯ , o T ∣ i 1 = q i , λ ) ⋅ π ] P(\mathcal O \mid \lambda) = \sum_{i=1}^{\mathcal K} \left[P(o_1,\cdots,o_T \mid i_1 = q_i,\lambda)\cdot \pi\right] P(O∣λ)=i=1∑K[P(o1,⋯,oT∣i1=qi,λ)⋅π] - 观察上式,想办法把 β 1 ( i ) \beta_1(i) β1(i)给凑出来。针对 P ( o 1 , ⋯ , o T ∣ i 1 = q i , λ ) P(o_1,\cdots,o_T \mid i_1 = q_i,\lambda) P(o1,⋯,oT∣i1=qi,λ),首先使用条件概率将 o 1 o_1 o1分离出来:
∑ i = 1 K [ P ( o 1 ∣ o 2 , ⋯ , o T , i 1 = q i , λ ) ⋅ P ( o 2 , ⋯ , o T ∣ i 1 = q i , λ ) ⋅ π ] \sum_{i=1}^{\mathcal K} \left[P(o_1 \mid o_2, \cdots,o_T,i_1 = q_i,\lambda) \cdot P(o_2, \cdots,o_T \mid i_1 = q_i,\lambda) \cdot \pi\right] i=1∑K[P(o1∣o2,⋯,oT,i1=qi,λ)⋅P(o2,⋯,oT∣i1=qi,λ)⋅π]
关于括号中的第一项,使用 观测独立性假设 进行简化:
实际上,在整个推导过程中,λ \lambda λ是可加可不加的,因为在‘求值问题’中,λ \lambda λ是已知的常量。
∑ i = 1 K [ P ( o 1 ∣ i 1 = q i , λ ) ⋅ P ( o 2 , ⋯ , o T ∣ i 1 = q i , λ ) ⋅ π ] \sum_{i=1}^{\mathcal K} [P(o_1 \mid i_1 = q_i,\lambda) \cdot P(o_2, \cdots,o_T \mid i_1 = q_i,\lambda) \cdot \pi] i=1∑K[P(o1∣i1=qi,λ)⋅P(o2,⋯,oT∣i1=qi,λ)⋅π]
观察括号中的第二项,它实际上就是 β 1 ( i ) \beta_1(i) β1(i)。而第一项使用发射矩阵 B \mathcal B B中的元素进行表示即: b i ( o 1 ) b_i(o_1) bi(o1)。
至此,已经找到了 P ( O ∣ λ ) P(\mathcal O \mid \lambda) P(O∣λ)和 β 1 ( i ) \beta_1(i) β1(i)之间的关联关系:
P ( O ∣ λ ) = ∑ i = 1 K [ b i ( o 1 ) ⋅ π ⋅ β 1 ( i ) ] P(\mathcal O \mid \lambda) = \sum_{i=1}^{\mathcal K} \left[b_i(o_1) \cdot \pi\cdot \beta_1(i) \right] P(O∣λ)=i=1∑K[bi(o1)⋅π⋅β1(i)]
β t ( i ) \beta_t(i) βt(i)和 β t − 1 ( j ) \beta_{t-1}(j) βt−1(j)之间的关联关系
观察 β t ( i ) \beta_t(i) βt(i)和 β t − 1 ( j ) \beta_{t-1}(j) βt−1(j)的展开结果:
β t ( i ) = P ( o t + 1 , ⋯ , o T ∣ i t = q i , λ ) β t − 1 ( i ) = P ( o t , ⋯ , o T ∣ i t − 1 = q j , λ ) \beta_t(i) =P(o_{t+1},\cdots,o_{T} \mid i_t = q_i,\lambda) \\ \beta_{t-1}(i) = P(o_{t},\cdots,o_{T} \mid i_{t-1} = q_j,\lambda) βt(i)=P(ot+1,⋯,oT∣it=qi,λ)βt−1(i)=P(ot,⋯,oT∣it−1=qj,λ)
- 首先观察 β t − 1 ( j ) \beta_{t-1}(j) βt−1(j),结合图像分析,状态变量 i t − 1 i_{t-1} it−1与观测变量 o t , ⋯ , o T o_t,\cdots,o_T ot,⋯,oT之间是不关联的,一个朴素思想是:引入状态变量 i t i_t it,将 i t − 1 , o t , ⋯ , o T i_{t-1},o_t,\cdots,o_T it−1,ot,⋯,oT关联起来:
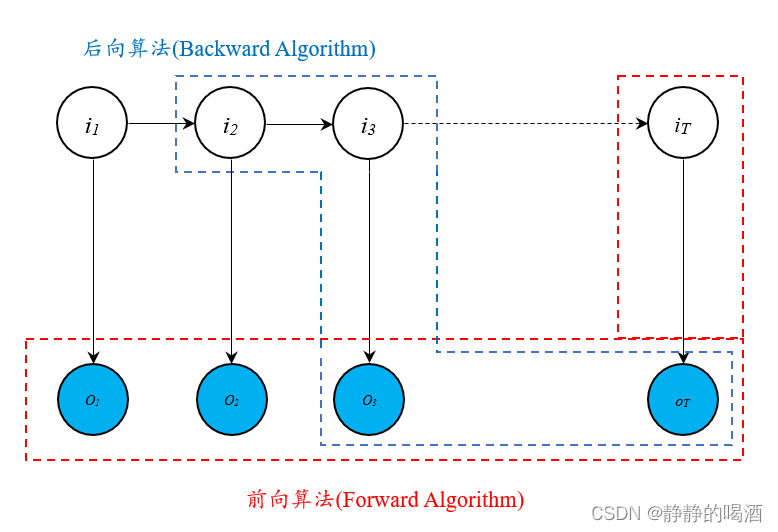
β t − 1 ( j ) = ∑ i t P ( o t , ⋯ , o T , i t = q i ∣ i t − 1 = q j , λ ) = ∑ i = 1 K P ( o t , ⋯ , o T , i t = q i ∣ i t − 1 = q j , λ ) \begin{aligned} \beta_{t-1}(j) & = \sum_{i_t}P(o_{t} ,\cdots,o_{T},i_t = q_i \mid i_{t-1} = q_j,\lambda) \\ & =\sum_{i=1}^{\mathcal K} P(o_{t} ,\cdots,o_{T},i_t = q_i \mid i_{t-1} = q_j,\lambda) \end{aligned} βt−1(j)=it∑P(ot,⋯,oT,it=qi∣it−1=qj,λ)=i=1∑KP(ot,⋯,oT,it=qi∣it−1=qj,λ) - 想办法凑出 i t i_t it和 i t − 1 i_{t-1} it−1之间的条件关系。即使用条件概率将 o t , ⋯ , o T o_t,\cdots,o_T ot,⋯,oT与 i t = q i i_t = q_i it=qi分离出来:
∑ i = 1 K [ P ( o t , ⋯ , o T ∣ i t = q i , i t − 1 = q j , λ ) ⋅ P ( i t = q i ∣ i t − 1 = q j , λ ) ] = ∑ i = 1 K [ P ( o t , ⋯ , o T ∣ i t = q i , i t − 1 = q j , λ ) ⋅ a i j ] \begin{aligned} & \sum_{i=1}^{\mathcal K} [P(o_t,\cdots,o_T \mid i_t = q_i,i_{t-1} = q_j,\lambda) \cdot P(i_t = q_i \mid i_{t-1} = q_j,\lambda)] \\ & = \sum_{i=1}^{\mathcal K} [P(o_t,\cdots,o_T \mid i_t = q_i,i_{t-1} = q_j,\lambda)\cdot a_{ij}] \end{aligned} i=1∑K[P(ot,⋯,oT∣it=qi,it−1=qj,λ)⋅P(it=qi∣it−1=qj,λ)]=i=1∑K[P(ot,⋯,oT∣it=qi,it−1=qj,λ)⋅aij] - 观察括号中的第一项,从概率图阻断的角度观察,亦或从观测独立的角度观察,状态变量 i t − 1 i_{t-1} it−1不可能与任意一个观测变量 o t , ⋯ , o T o_t,\cdots,o_T ot,⋯,oT存在关系。因此,第一项可表示为: P ( o t , ⋯ , o T ∣ i t = q i ) P(o_t,\cdots,o_T \mid i_t = q_i) P(ot,⋯,oT∣it=qi)。对应结果整理如下:
i t − 1 i_{t-1} it−1和后续观测变量结点均属于‘顺序结构’。由于i t i_t it的阻塞性,o 1 , ⋯ , o T o_1,\cdots,o_T o1,⋯,oT均与i t − 1 i_{t-1} it−1条件独立。传送门
β t − 1 ( j ) = ∑ i = 1 K [ P ( o t , ⋯ , o T ∣ i t = q i , λ ) ⋅ a i j ] \beta_{t-1}(j) = \sum_{i=1}^{\mathcal K}[P(o_t,\cdots,o_T \mid i_t = q_i,\lambda) \cdot a_{ij}] βt−1(j)=i=1∑K[P(ot,⋯,oT∣it=qi,λ)⋅aij] - 基于上式,凑出观测独立性假设步骤。将 o t o_t ot提到前面,则有:
∑ i = 1 K [ P ( o t ∣ o t + 1 , ⋯ , o T , i t = q i , λ ) ⋅ P ( o t + 1 , ⋯ , o T ∣ i t = q i , λ ) ⋅ a i j ] \sum_{i=1}^{\mathcal K} [P(o_t \mid o_{t+1},\cdots,o_T,i_t = q_i,\lambda)\cdot P(o_{t+1},\cdots,o_T \mid i_t = q_i,\lambda) \cdot a_{ij}] i=1∑K[P(ot∣ot+1,⋯,oT,it=qi,λ)⋅P(ot+1,⋯,oT∣it=qi,λ)⋅aij] - 根据 观测独立性假设,第一项 P ( o t ∣ o t + 1 , ⋯ , o T , i t = q i , λ ) = P ( o t ∣ i t = q i , λ ) P(o_t \mid o_{t+1},\cdots,o_T,i_t = q_i,\lambda) = P(o_t \mid i_t= q_i,\lambda) P(ot∣ot+1,⋯,oT,it=qi,λ)=P(ot∣it=qi,λ)。并且第二项就是之前定义的 β t ( i ) \beta_{t}(i) βt(i)。最终迭代结果整理如下:
β t − 1 ( j ) = ∑ i = 1 K P ( o t ∣ i t = q i , λ ) ⋅ β t ( i ) ⋅ a i j = ∑ i = 1 K b i ( o t ) ⋅ β t ( i ) ⋅ a i j \begin{aligned} \beta_{t-1}(j) & = \sum_{i=1}^{\mathcal K} P(o_t \mid i_t = q_i,\lambda) \cdot \beta_t(i) \cdot a_{ij} \\ & = \sum_{i=1}^{\mathcal K} b_i(o_t) \cdot \beta_t(i) \cdot a_{ij} \end{aligned} βt−1(j)=i=1∑KP(ot∣it=qi,λ)⋅βt(i)⋅aij=i=1∑Kbi(ot)⋅βt(i)⋅aij
至此,得到了 β t − 1 ( j ) \beta_{t-1}(j) βt−1(j)和 β t ( i ) \beta_{t}(i) βt(i)之间的递归关系。
观察后向算法 需要的时间复杂度:
- 得到 β 1 ( i ) \beta_1(i) β1(i)需要的时间复杂度是 O ( K × T ) O(\mathcal K \times T) O(K×T);
- 通过公式: P ( O ∣ λ ) = ∑ i = 1 K [ b i ( o 1 ) ⋅ π ⋅ β 1 ( i ) ] P(\mathcal O \mid \lambda) = \sum_{i=1}^{\mathcal K} \left[b_i(o_1) \cdot \pi\cdot \beta_1(i) \right] P(O∣λ)=∑i=1K[bi(o1)⋅π⋅β1(i)]需要的时间复杂度是 O ( K ) O(\mathcal K) O(K)
- 因此后向算法的时间复杂度和前向算法相同,均是 O ( K 2 × T ) O(\mathcal K^2 \times T) O(K2×T)。
下一节将介绍隐马尔可夫模型的参数 λ \lambda λ求解问题