前言
作者:小蜗牛向前冲
名言:我可以接收失败,但我不能接收放弃
如果觉的博主的文章还不错的话,还请
点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正。
为了提高自己编写代码的能力,特意开设刷题专题,记录自己刷题的思路和理解。欢迎❀大家的指正。
在下面的解题中我们都用C语言实现。
1用队列实现栈
在这里我们就是要将队列模拟实现成栈,我们知道队列是先进先出,栈是先进后出;那我们又如何实现呢?其实我们可以借助二个队列实现。下面我们借助图像来理解一下:
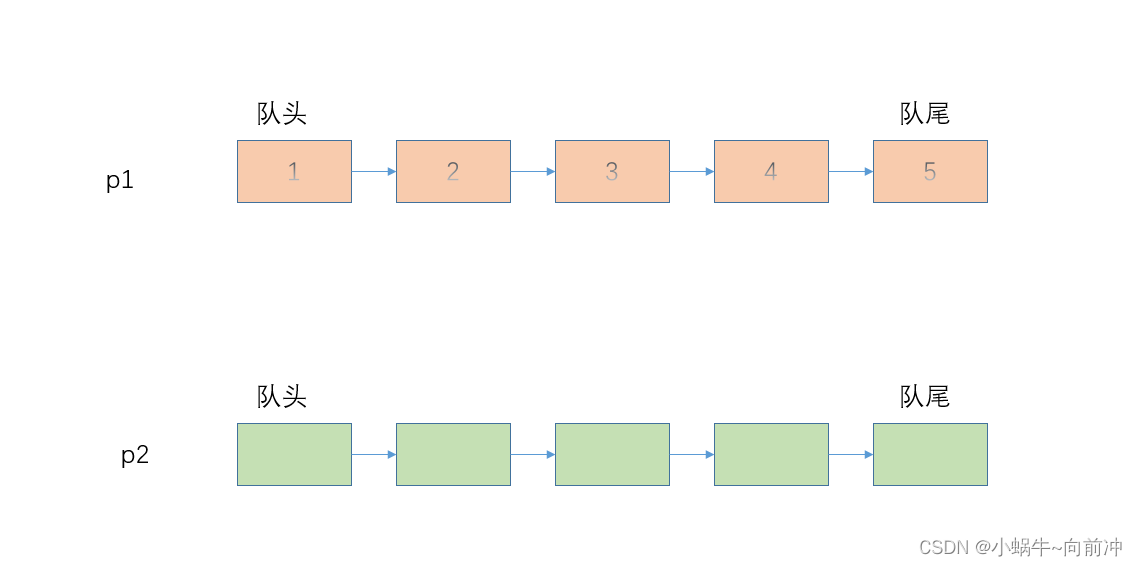
首先我们建立二个队列p1,p2,我们可能理解为入栈我们就将入数据到p1处。
其次,我们可以认为p2队列是用来中间存放数据的。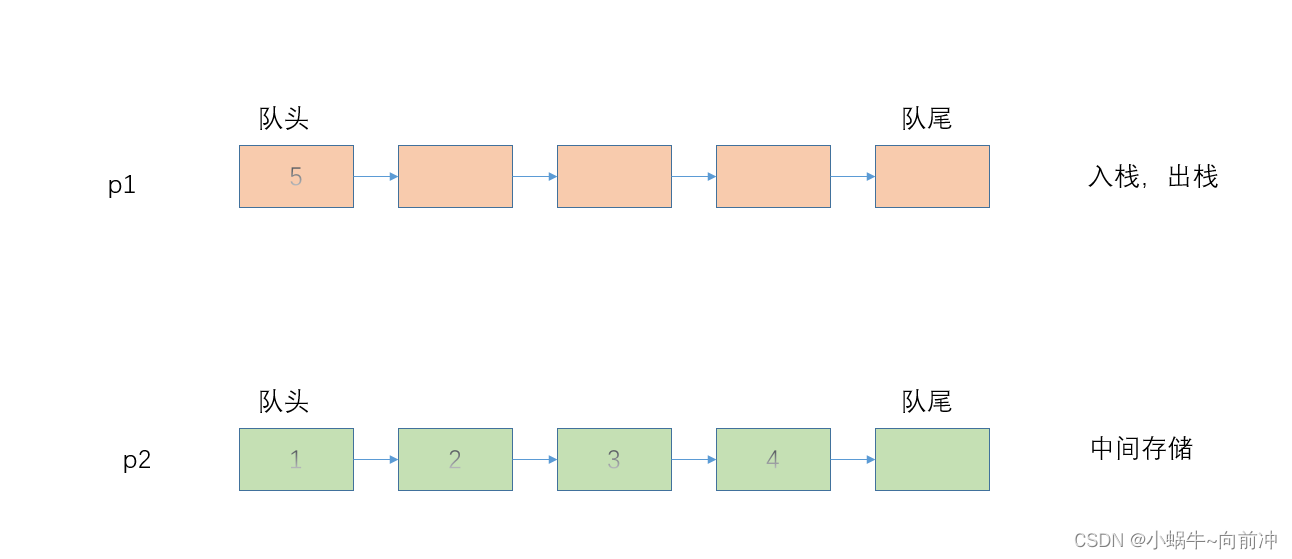
这样我们就成功将5出栈了,如果要将4出栈,那么我们又得需要将p2中的数据倒入到p1中:
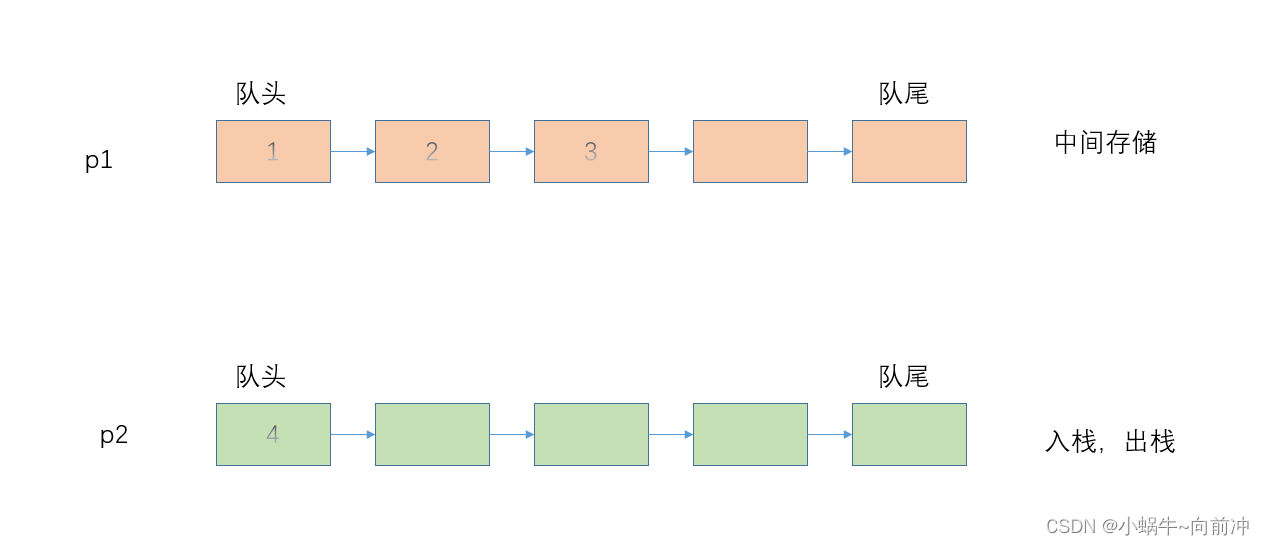
这样我们就完成了4出栈。
下面我们简单总结一下思路:
1我们要建立二个队列经行模拟。
2始终保持一个队列为空,在出栈时,将将n-1个数据都倒入到空队列中,那么留在另个队列的数据就可以直接出栈了。
下面是完成的解题代码:
typedef int QDataType;
//定义队列
typedef struct QueueNode
{
QDataType data;//数据类型
struct QueueNode* next;
}QNode;
//定义指向头和尾的二个指针
typedef struct Queue
{
QNode* head;
QNode* tail;
int size;
}Queue;
//初始化
void QueueInit(Queue* pq);
//销毁
void QueueDestroy(Queue* pq);
//入队
void QueuePush(Queue* pq, QDataType x);
//出队
void QueuePop(Queue* pq);
//返回指向队头的数据的指针
QDataType QueueFront(Queue* pq);
//返回指向队尾的数据的指针
QDataType QueueBack(Queue* pq);
//判断队列是否为空
bool QueueEmpty(Queue* pq);
//返回队列的大小
int QueueSize(Queue* pq);
//初始化
void QueueInit(Queue* pq)
{
assert(pq);
pq->head = pq->tail = NULL;
pq->size = 0;
}
//销毁
void QueueDestroy(Queue* pq)
{
assert(pq);
QNode* cur = pq->head;
while (cur)
{
QNode* del = cur;
cur = cur->next;//指向下个节点
free(del);
}
pq->head = pq->tail = NULL;//防止出现野指针
pq->size = 0;
}
//入队
void QueuePush(Queue* pq, QDataType x)
{
assert(pq);
//申请节点
QNode* newNode = (QNode*)malloc(sizeof(QNode));
if (newNode==NULL)
{
perror("malloc fail");
exit(-1);
}
else
{
newNode->data = x;
newNode->next = NULL;
}
//队列为空
if (pq->tail == NULL)
{
pq->head = pq->tail = newNode;
}
//不为空
else
{
pq->tail->next = newNode;
pq->tail = newNode;//tail指针指向newNode
}
pq->size++;
}
//出队
void QueuePop(Queue* pq)
{
assert(pq);
//断言队列是否为空
assert(!QueueEmpty(pq));
//当队列中就一个数据时
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QNode* del = pq->head;
pq->head = pq->head->next;//头变为下个节点
free(del);
del = NULL;
}
pq->size--;
}
//判断队列是否为空
bool QueueEmpty(Queue* pq)
{
assert(pq);
return pq->tail == NULL;
}
//返回指向队头的数据的指针
QDataType QueueFront(Queue* pq)
{
assert(pq);
//断言队列是否为空
assert(!QueueEmpty(pq));
return pq->head->data;
}
//返回指向队尾的数据的指针
QDataType QueueBack(Queue* pq)
{
assert(pq);
//断言队列是否为空
assert(!QueueEmpty(pq));
return pq->tail->data;
}
//返回队列的大小
int QueueSize(Queue* pq)
{
return pq->size;
}
typedef struct {
Queue p1;//入栈
Queue p2;//出栈
} MyStack;
MyStack* myStackCreate() {
MyStack* obj = (MyStack*)malloc(sizeof(MyStack));
//对栈初始化
QueueInit(&obj->p1);
QueueInit(&obj->p2);
return obj;
}
void myStackPush(MyStack* obj, int x) {
//当p1为空时就将数据倒入
if(!QueueEmpty(&obj->p1))
{
QueuePush(&obj->p1,x);
}
else
{
QueuePush(&obj->p2,x);
}
}
int myStackPop(MyStack* obj) {
Queue* empty = &obj->p1;//假设p1为空
Queue* noEmpty = &obj->p2;
//如果p1队列为非空
if(!QueueEmpty(&obj->p1))
{
empty = &obj->p2;
noEmpty = &obj->p1;
}
//将非空队列中的N-1的数据都倒入到空队列中,那么原队列还剩的1个数据就是要返回的栈顶数据
while(QueueSize(noEmpty)>1)
{
QueuePush(empty,QueueFront(noEmpty));//入栈
QueuePop(noEmpty);//出栈
}
int top = QueueFront(noEmpty);
QueuePop(noEmpty);//出栈
return top;
}
int myStackTop(MyStack* obj) {
if(!QueueEmpty(&obj->p1))
{
return QueueBack(&obj->p1);
}
else
{
return QueueBack(&obj->p2);
}
}
bool myStackEmpty(MyStack* obj) {
return QueueEmpty(&obj->p1) && QueueEmpty(&obj->p2);
}
void myStackFree(MyStack* obj) {
QueueDestroy(&obj->p1);
QueueDestroy(&obj->p2);
free(obj);
}
2 栈实现队列

要用二个栈实现队列,这是很好实现的。
为什么这么说呢?我们可以用栈PushST来模拟入队列,栈PopST模拟出队列。
下面我们顺着这个思路来,来图解一下 1,2,3,4的入队列和出队列的过程。
1数据入队列
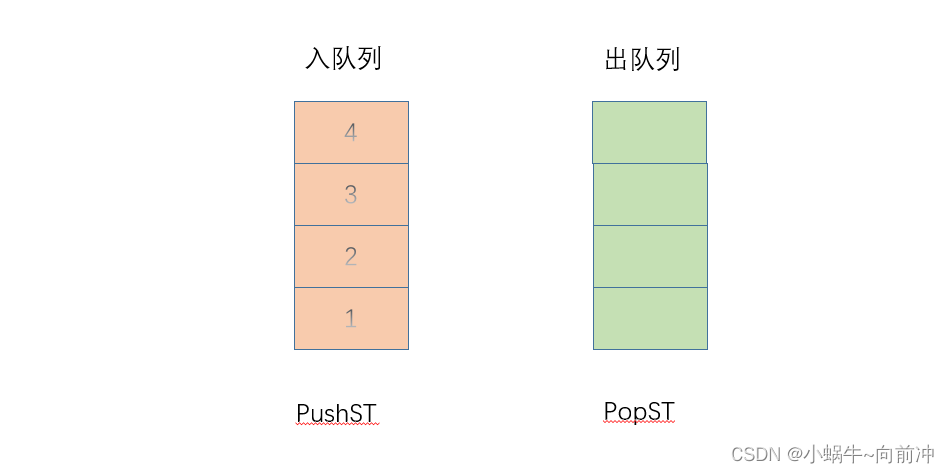
2 要出队列时,当PopST为空的时候,就将PushST的数据倒入到PopST中,然后直接出就行。
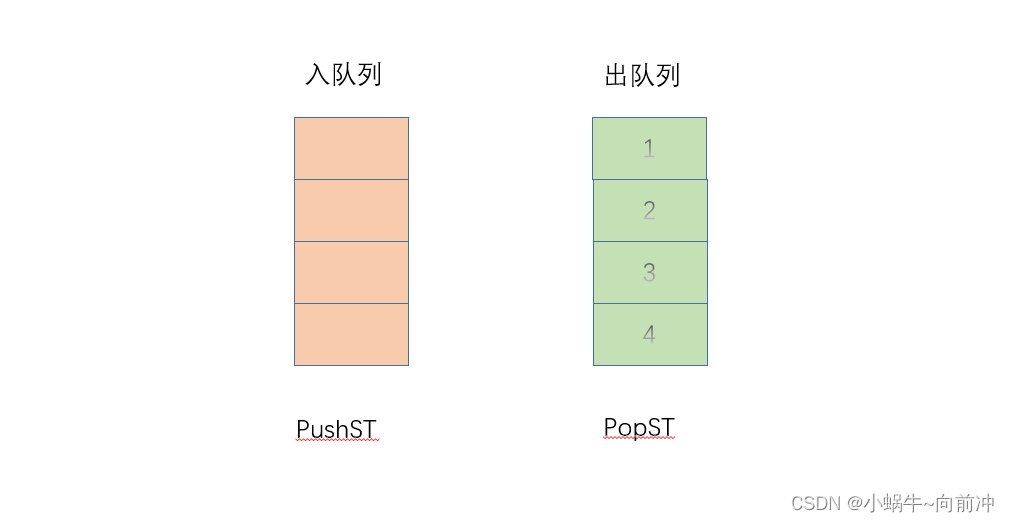
完整代码:
typedef int STDataType;
//定义栈
typedef struct Stack
{
STDataType* arr;//数据类型
int pos;//数组下标
int capacity;//栈的容量
}ST;
//初始化
void StackInit(ST* ps);
//销毁
void StackDestroy(ST* ps);
//入栈
void StackPush(ST* ps, STDataType x);
//出栈
void StackPop(ST* ps);
显示返回栈顶数据
STDataType StackTop(ST* ps);
//判断栈是否为空
bool StackEmpty(ST* ps);
//返回栈的长度//初始化
void StackInit(ST* ps)
{
assert(ps);
ps->arr = NULL;//初始数组为空
ps->pos = ps->capacity = 0;//初始为0
}
//销毁
void StackDestroy(ST* ps)
{
assert(ps);
free(ps->arr);//arr是整个栈的地址
ps->arr = NULL;
ps->capacity = ps->pos = 0;
}
//入栈
void StackPush(ST* ps, STDataType x)
{
assert(ps);
//判断栈的空间是否满
if (ps->pos == ps->capacity)
{
//扩容
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;//扩2倍
STDataType* tmp = (STDataType*)realloc(ps->arr, newCapacity * sizeof(STDataType));
if (tmp == NULL)
{
perror("reamlloc fail");
exit(-1);
}
//跟新容量
ps->arr = tmp;
ps->capacity = newCapacity;
}
//入栈
ps->arr[ps->pos] = x;
ps->pos++;//下标++
}
//出栈
void StackPop(ST* ps)
{
assert(ps);
//断言栈是否为空
assert(!StackEmpty(ps));
--ps->pos;
}
//判断栈是否为空
bool StackEmpty(ST* ps)
{
assert(ps);
return ps->pos == 0;
}
//显示返回栈顶数据
STDataType StackTop(ST* ps)
{
assert(ps);
//断言栈是否为空
assert(!StackEmpty(ps));
return ps->arr[ps->pos - 1];//下标已经前移
}
//返回栈的长度
int StackSize(ST* ps)
{
assert(ps);
return ps->pos;
}
int StackSize(ST* ps);
typedef struct {
ST PushST;//入队列
ST PopST;//出队列
} MyQueue;
MyQueue* myQueueCreate() {
//为模拟的队列开辟空间
MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
//初始化
StackInit(&obj->PushST);
StackInit(&obj->PopST);
return obj;
}
void myQueuePush(MyQueue* obj, int x) {
StackPush(&obj->PushST, x);
}
void PushSTTOPopST(MyQueue* obj)
{
//判断PopST是否为空
if (StackEmpty(&obj->PopST))
{
while (!(StackEmpty(&obj->PushST)))
{
StackPush(&obj->PopST, StackTop(&obj->PushST));
StackPop(&obj->PushST);
}
}
}
int myQueuePop(MyQueue* obj) {
//将PuahST中的元素都倒入PopST中
PushSTTOPopST(obj);
int fornt = StackTop(&obj->PopST);
StackPop(&obj->PopST);
return fornt;
}
int myQueuePeek(MyQueue* obj) {
//将PuahST中的元素都倒入PopST中
PushSTTOPopST(obj);
return StackTop(&obj->PopST);
}
bool myQueueEmpty(MyQueue* obj) {
return StackEmpty(&obj->PushST) && StackEmpty(&obj->PopST);
}
void myQueueFree(MyQueue* obj) {
//销毁空间
StackDestroy(&obj->PushST);
StackDestroy(&obj->PushST);
free(obj);
}
3 设计循环队列
对于设计循环队列来说有二种思路:
1 用数组实现
2 用链表实现
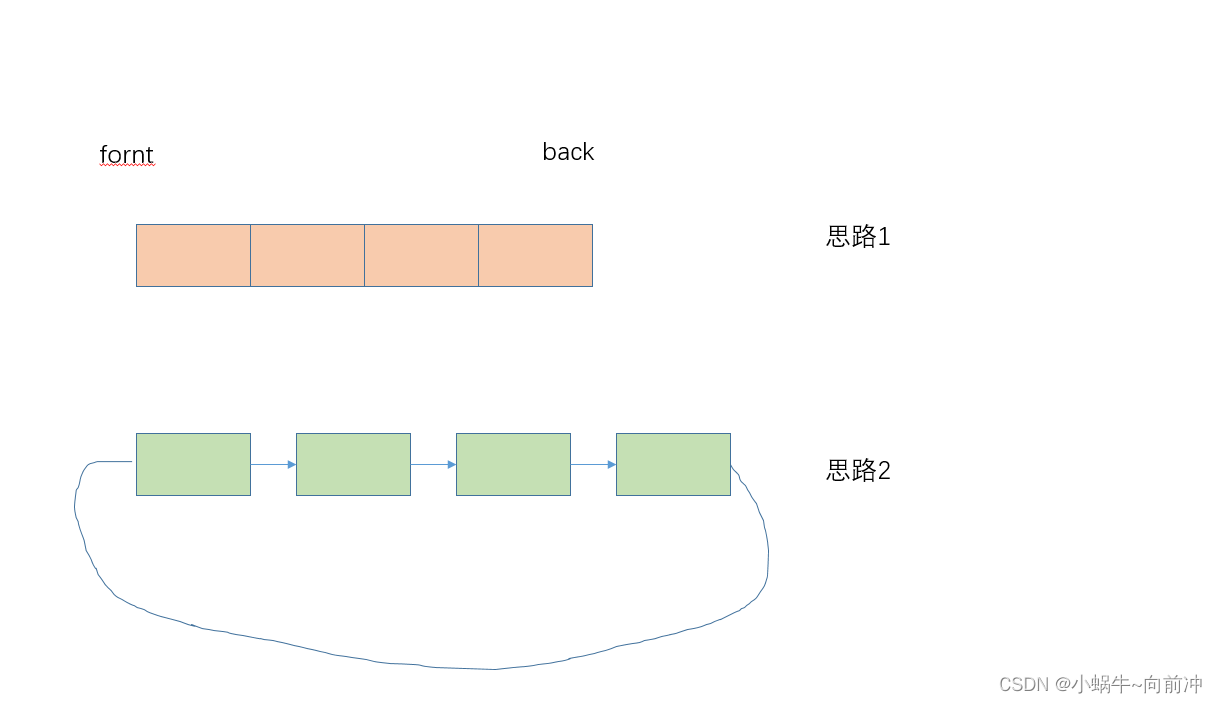
对于这二种思路,我会首选思路1,为什么会这么说呢?
因为用链表实现循环队列,首先你要malloc多份空间,而且这样你还不好判断循环队列是否已满!
所以:我会选择用思路1来为大家解题。
此题有个重点:那就是如何判断队列是否以满。
因为在对于空和满来说,队列中指针fornt和back都是指向同一个位置。
那么我们这么去解决呢?
我们有二个思路:
1多开辟一块空间
2用size标记队列的长度,当size==k时就满
下面我们用思路1来解决:

代码转换:
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->back + 1) % obj->n == obj->fornt;
}完整代码:
typedef struct {
int* arr;
int fornt;
int back;
int n;
} MyCircularQueue;
MyCircularQueue* myCircularQueueCreate(int k) {
MyCircularQueue* obj = (MyCircularQueue*)malloc(sizeof(MyCircularQueue));
obj->arr = (int*)malloc(sizeof(int) * (k + 1));
obj->fornt = obj->back=0;
obj->n = k + 1;
return obj;
}
bool myCircularQueueIsEmpty(MyCircularQueue* obj) {
return obj->fornt == obj->back;
}
bool myCircularQueueIsFull(MyCircularQueue* obj) {
return (obj->back + 1) % obj->n == obj->fornt;
}
bool myCircularQueueEnQueue(MyCircularQueue* obj, int value) {
if (myCircularQueueIsFull(obj))
{
return false;
}
obj->arr[obj->back] = value;
obj->back++;
//如果back指针已经指向尾,需要重新指向头
obj->back %= obj->n;
return true;
}
bool myCircularQueueDeQueue(MyCircularQueue* obj) {
if (myCircularQueueIsEmpty(obj))
{
return false;
}
obj->fornt++;
//如果fornt指针已经指向尾,需要重新指向头
obj->fornt %= obj->n;
return true;
}
int myCircularQueueFront(MyCircularQueue* obj) {
if (myCircularQueueIsEmpty(obj))
{
return -1;
}
return obj->arr[obj->fornt];
}
int myCircularQueueRear(MyCircularQueue* obj) {
if (myCircularQueueIsEmpty(obj))
{
return -1;
}
else if(obj->back==0)
return obj->arr[obj->n-1];
else
return obj->arr[obj->back-1];
// return obj->arr[(obj->back -1 + obj->n) % obj->n];
}
void myCircularQueueFree(MyCircularQueue* obj) {
free(obj->arr);
free(obj);
}
