【线性代数】MIT Linear Algebra Lecture 4: Factorization into A = LU

Author｜ Rickyの水果摊

Time ｜ 2022.9.6

Lecture 4: Factorization into A = LU

Lecture Info

1. Instructor: Prof. Gilbert Strang

2. Course Number: 18.06

3. Topics: Linear Algebra

4. Official Lecture Resource: Resource Index of Linear Algebra

Excellent Notes on GitHub

There are some classic, excellent notes from other authors on GitHub, wihch I highly recommend you to star ⭐️ and read 📖

notes-linear-algebra (A systematic notes written in Chinese)

The-Art-of-Linear-Algebra (Focus on visualization of important concept of Linear Algebra)

Video Link

Lecture 4: Factorization into A = LU (bilibili)

Lecture 4: Factorization into A = LU (YouTube)

Key Points

1. factorization into $A=LU$
2. cost of elimination
3. permutations

Active Recall Questions

1. What’s the premise when we talk about matrix factorization ?
2. Why we prefer $A=LU$ than $EA=U$ ? (Hint: compare $L$ and $E$ with a specific example)
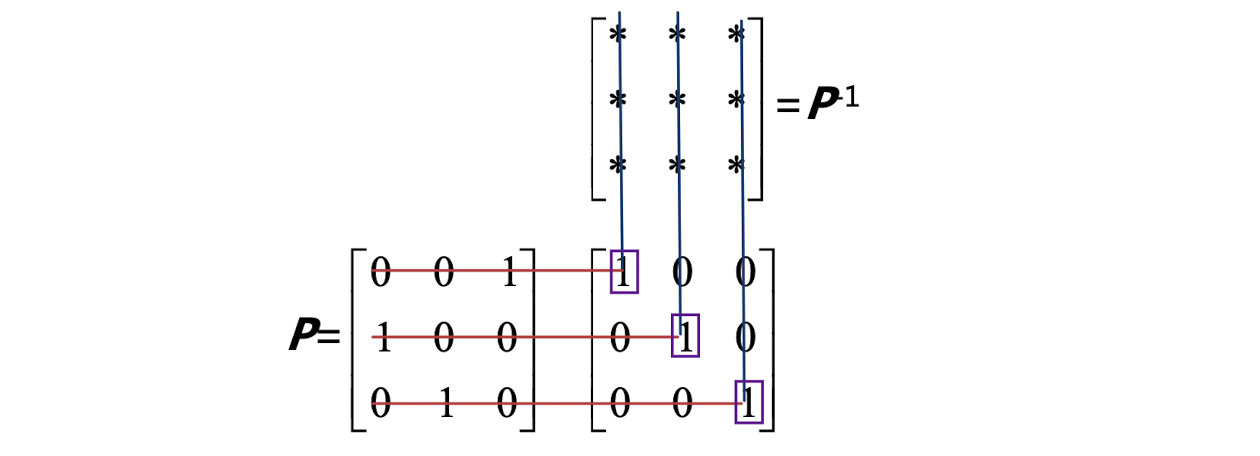
3. For permutations, why $P^{-1}=P^T$ ? (Hint: $P\ast P^{-1}=I$ , how to get those specific 1s on $I$ by perspective of first way of matrix multiplication)

Answer

1. no row exchanges (or no permutation matrices) when elimination is implemented
2. blogpost that explains this question
3. Here is the derivation:
   1. On the example given in the figure below, in order to get the first 1 on $I$, the first column $co{l}_1$ of $P^{-1}$ must be $\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$, which is exactly the first column $co{l}_1$ of $P^T$, so that $\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\ast \left[\begin{array}{ccc}0& 0& 1\end{array}\right]=1$.
   2. same principle for the next 2 columns. Therefore, we can understand $P^T=P^{-1}$ intuitively