目录
一.定义
如果函数调用它本身,那么此函数就是递归的。
二.递归的两个必要条件
- 存在限制条件,当满足这个限制条件时,递归便不再继续
- 每次递归调用后,越来越接近这个限制条件
三.青蛙跳台阶
问题:
一只青蛙一次可以跳上 1 级台阶,也可以跳上2 级。求该青蛙跳上一个n 级的台阶总共有多少种跳法?
分析:
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| sum | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 |
当青蛙要n==1的时候,只要跳1级一种方法;
n==2时,可以跳两个1级和一个2级;
n==3时,它的前一跳可能是n==1,也可能是n==2,计算n==1和n==2时共有几种跳法即可
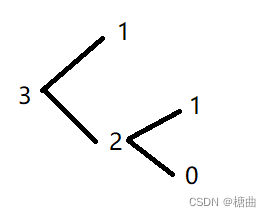
当我们需要知道它n级台阶有几种跳法时,计算n-1和n-2的跳法和即可((n-1)+(n-2))
依次类推计算n-1和n-2的跳法,也就是从0级跳到1级和从0级跳到2级的总和
代码:
int text(int n)
{
if (n == 2)//当n减到2时共2种跳法
return 2;
if (n == 1)//减到1时1种跳法
return 1;
int count = text(n - 1) + text(n - 2);
return count;
}
int main()
{
int n = 0;
int count = 0;
scanf("%d", &n);
printf("%d", text(n));
return 0;
}代码优化后为:
int text(int n)
{
if (n <= 2)
return n;
return text(n - 1) + text(n - 2);
}
int main()
{
int n = 0;
int count = 0;
scanf("%d", &n);
printf("%d", text(n));
return 0;
}使用循环解决
int text1(int n)
{
if (n <= 2)
return n;
int sum = 0;
int a = 1;//将n-1和n-2放入变量a和b
int b = 2;
for (int i = 3; i <= n; i++)
{
sum = a + b;
a = b;
b = sum;
}
return sum;
}
int main()
{
int n = 0;
int count = 0;
scanf("%d", &n);
printf("%d", text1(n));
return 0;
}四.汉诺塔问题
问题:
有三根杆子A,B,C。A杆上有n只盘子。每次移动一块盘子,小的只能叠在大的上面,把所有盘子从A杆经B杆全部移动到C杆上。
分析:
- 把n-1个盘子从A杆经C杆移动到B杆
- 将A杆上的第n个盘子移动到C杆
- 然后再将n-1个盘子从B杆经A杆移到C杆(此时的B杆看作操作1的A杆,A杆看作B杆)
假设现在A杆上有3个盘子,那我们要如何来放呢?
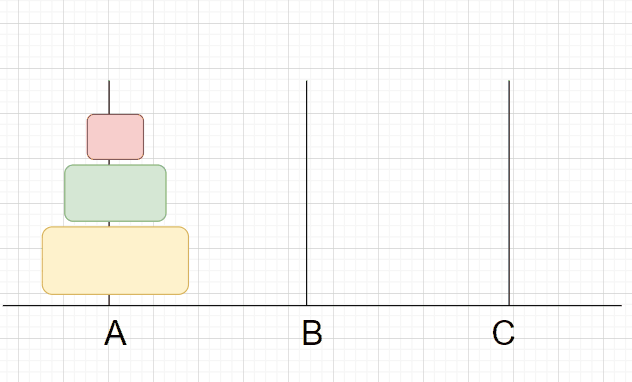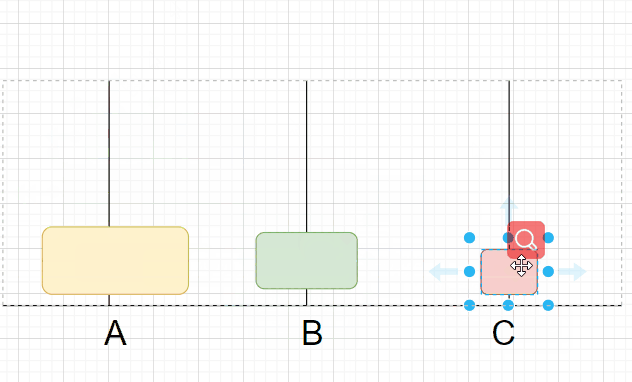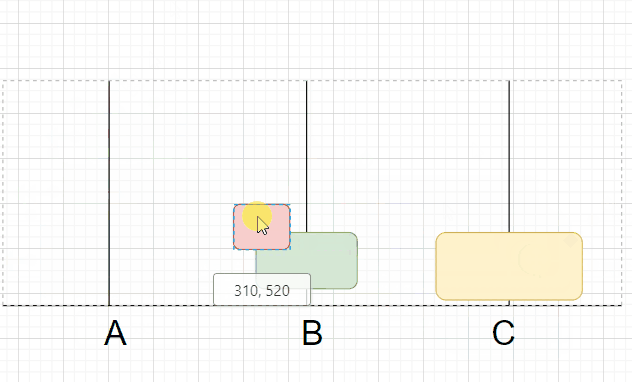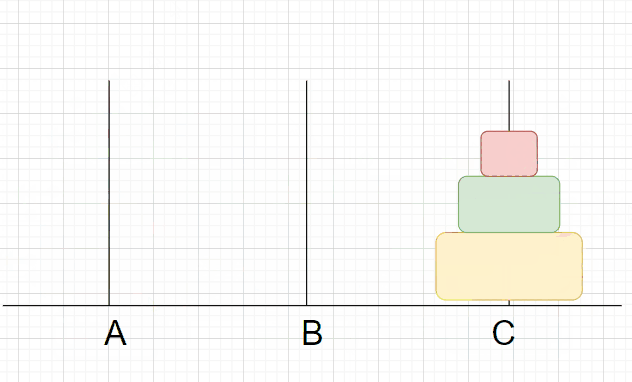
这时,B杆上只有两个盘子,我们将此时的B杆看作最开始还未移动的A杆,之前A杆将n-1个盘子经由C杆移动到B,现在将B杆n-2个盘子经C杆移动到A杆,在将第n-1个盘子移动到C杆。如此循环直到最后。
我们先尝试写出1-4阶汉诺塔的移动步骤:
| 阶数 | 步骤 |
| 1 | A->C |
| 2 | A->B, A->C, B->C |
| 3 | A->C, A->B, C->B, B->A, B->C, A->C |
| 4 | A->B, A->C, B->C, A->B, C->A, C->B, A->B, A->C,B->C,B->A, C->A, B->C, A->B, A->C, B->C |
函数介绍:
void hanoi(int n,char A,char B,char C);这个函数的参数对应的功能如下:
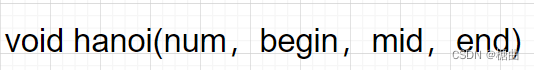
我们每次移动的方向和数量为:begin 向 end 移动 num-1个盘子
这样就可以完成如下三步:
- 将num-1个盘子从begin移动到mid
- 将最后一个盘子从begin移动到end
- 再将num-1个盘子从mid移动到end
我们可以得到如下图画(num=3):
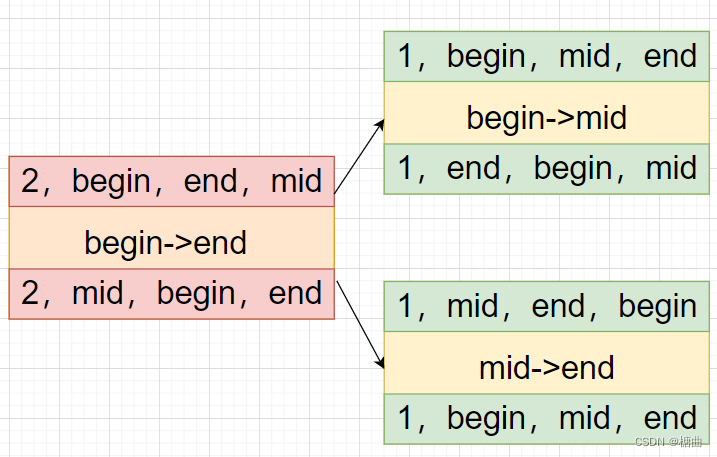
完整代码:
void hanoi(int n, char A, char B, char C)
{
if (n == 1)
printf("%c->%c\n", A, C);
else
{
hanoi(n - 1, A, C, B);
printf("%c->%c\n", A, C);
hanoi(n - 1, B, A, C);
}
}
int main()
{
int n = 0;
printf("请输入盘子的数量:");
scanf("%d", &n);
hanoi(n, 'A', 'B', 'C');
return 0;
}那么三阶递归的完全展开式就是下图:
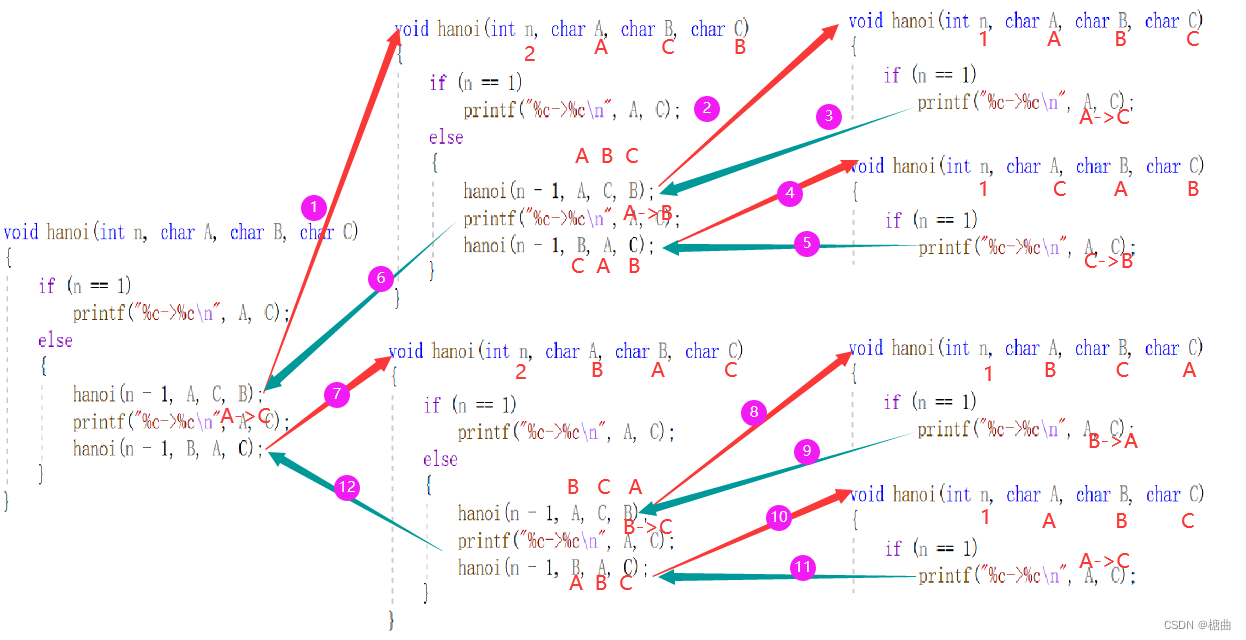
本文含有隐藏内容,请 开通VIP 后查看