1.概念：

高斯滤波是一种线性平滑滤波，适用于消除高斯噪声，广泛应用于图像处理的减噪过程。通俗的讲，高斯滤波就是对整幅图像进行加权平均的过程，每一个像素点的值，都由其本身和邻域内的其他像素值经过加权平均后得到。高斯滤波的具体操作是：用一个模板（或称卷积、掩模）扫描图像中的每一个像素，用模板确定的邻域内像素的加权平均灰度值去替代模板中心像素点的值。

2.实质：一种信号的滤波器

高斯滤波(Gauss filter)实质上是一种信号的滤波器，其用途为信号的平滑处理，数字图像用于后期应用，其噪声是最大的问题，因为误差会累计传递等原因，大多图像处理教材会在很早的时候介绍Gauss滤波器，用于得到信噪比SNR较高的图像（反应真实信号）。高斯平滑滤波器对于抑制服从正态分布的噪声非常有效。

3.高斯分布公式

一维高斯分布：

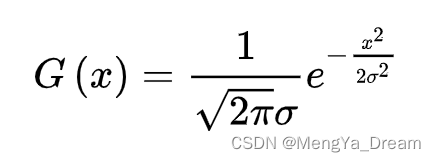
二维高斯分布：

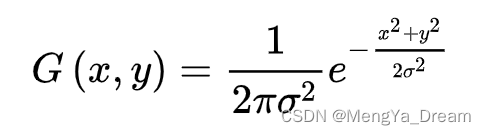
4.图像里的高斯-尺度空间理论

公式化：

假设二维图像为f(x,y)，二维高斯函数（关于t的簇）为g(x,y;t)，那么线性尺度空间就可以通过二者卷积（Convolution）得到：L(⋅,⋅;t)=g(⋅,⋅;t)∗f(⋅,⋅)，高斯滤波器的方差 t=被称为尺度参数。

，如果较小，那么生成的模板的中心系数较大，而周围的系数较小，这样对图像的平滑效果就不是很明显;反之，较大，则生成的模板的各个系数相差就不是很大，比较类似均值模板，对图像的平滑效果比较明显。

图示计算方式：

• 均值滤波：所有像素相加/9 =中间
• 高斯滤波：每个像素对应一个系数，即分配权重，对应相乘，也就是所谓的点乘dot。
• 高斯滤波重点在于每个点的权重是不一样的。

可视化展示：

高斯滤波器的方差 t=被称为尺度参数：

直观地看，图像中尺度小于√t的结构会被平滑地无法分辨。因此，t越大，平滑越剧烈。
实际上，我们只会考虑t≥0的一些离散取值。当t=0时，高斯滤波器退化为脉冲函数（impulse function），因此卷积的结果是图像本身，不作任何平滑。

事实上，还可以构造其他尺度空间。
但由于线性（高斯）尺度空间满足很多很好的性质，因此是使用最为广泛的。

尺度空间方法最重要的属性是尺度不变性（scale invariant），使可以处理未知大小的图像目标。

最后要注意的是，在构造尺度空间时，往往还伴随着降采样。
比如t=2的尺度空间，会将其分辨率减半，即面积减为1/4。

其他案例学习：混合高斯模型