目录
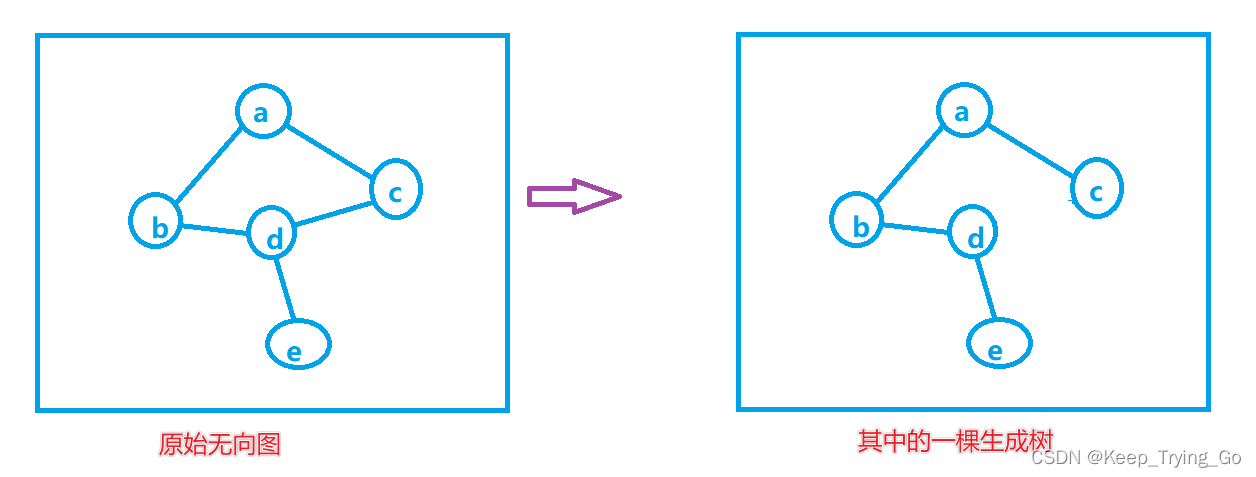
1.生成树
连通图的生成树:包含图中全部顶点的一个极小连通子图。
若图中的顶点数为n,则它的生成树包含n-1条边。如果一个图中有n个顶点和小于n-1条边,则是非连通图。如果它多于n-1条边,则一定存在环。
如果一个连通图本身就是一棵树,那么其最小生成树就是本身;
只有连通图才有生成树,非连通图只有生成森林。
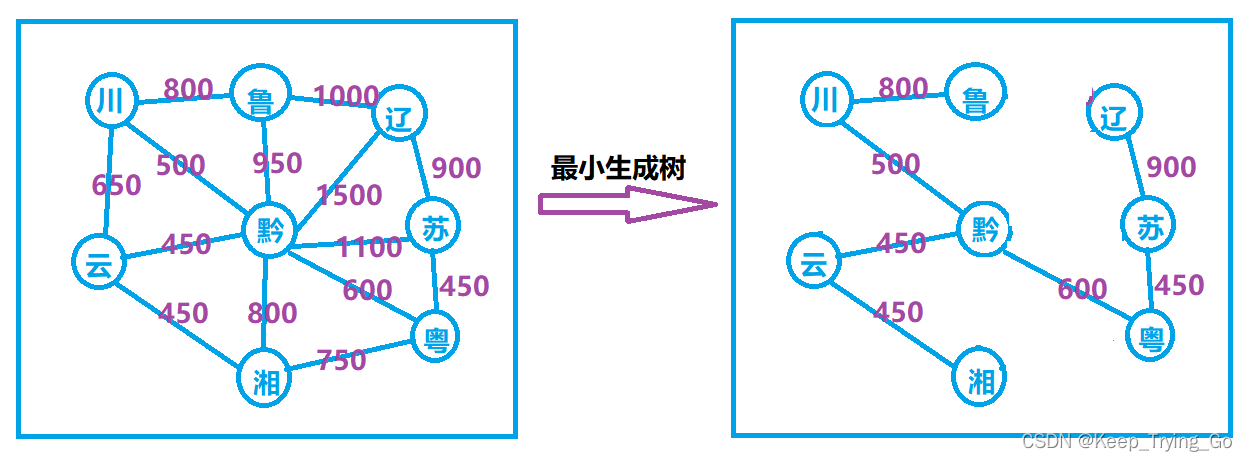
2.最小生成树
通过克鲁斯卡尔(Kruskal)算法求解最小生成树:
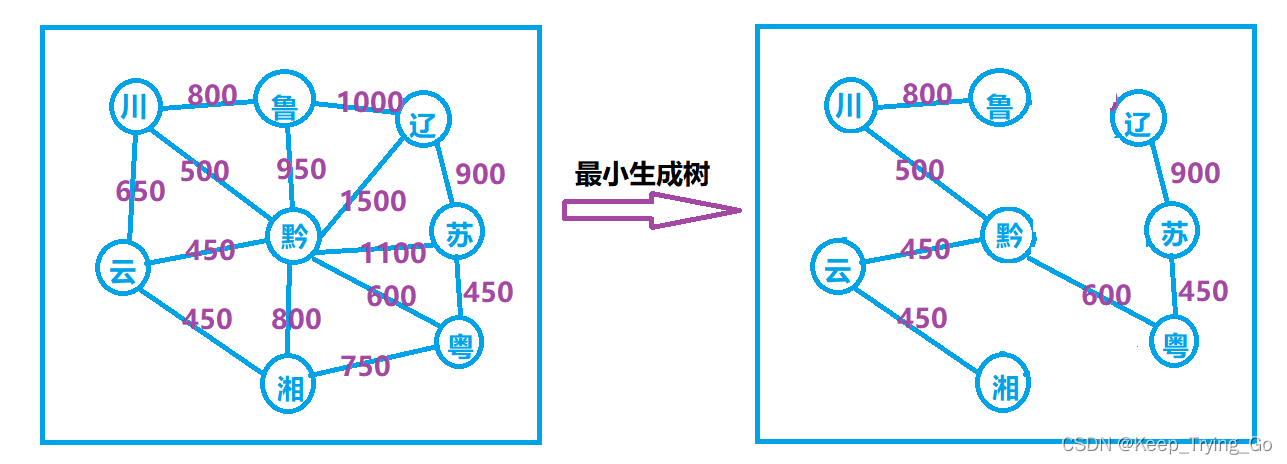
注:以上的距离标识都不是真实的。
最小生成树可能有多个,但边的权值之和总是唯一最小的;
最小生成树的边数=顶点数-1。
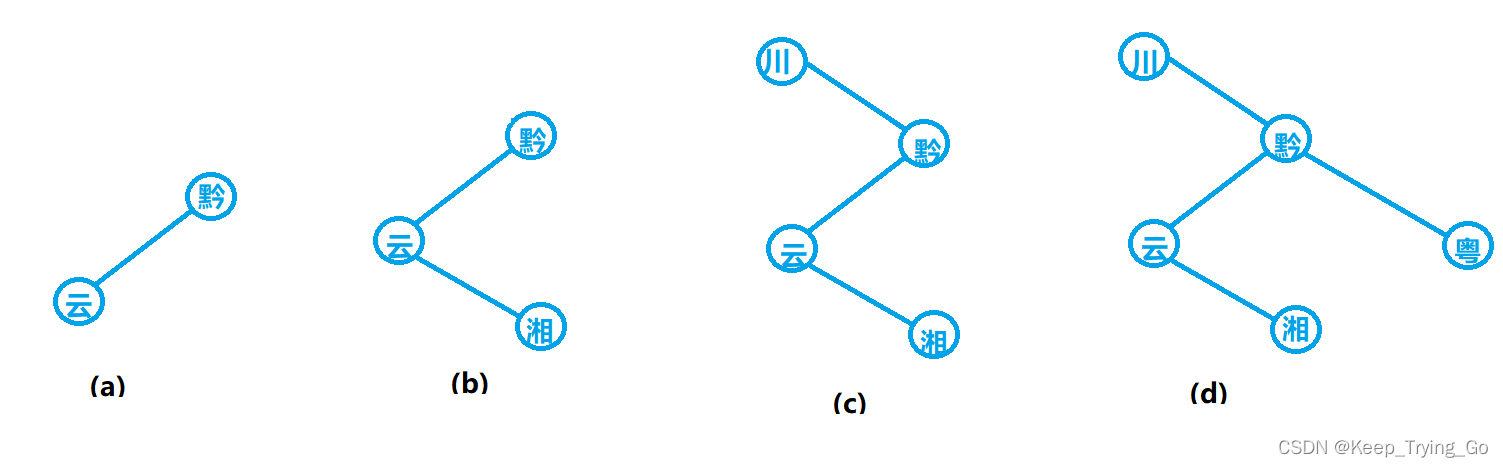
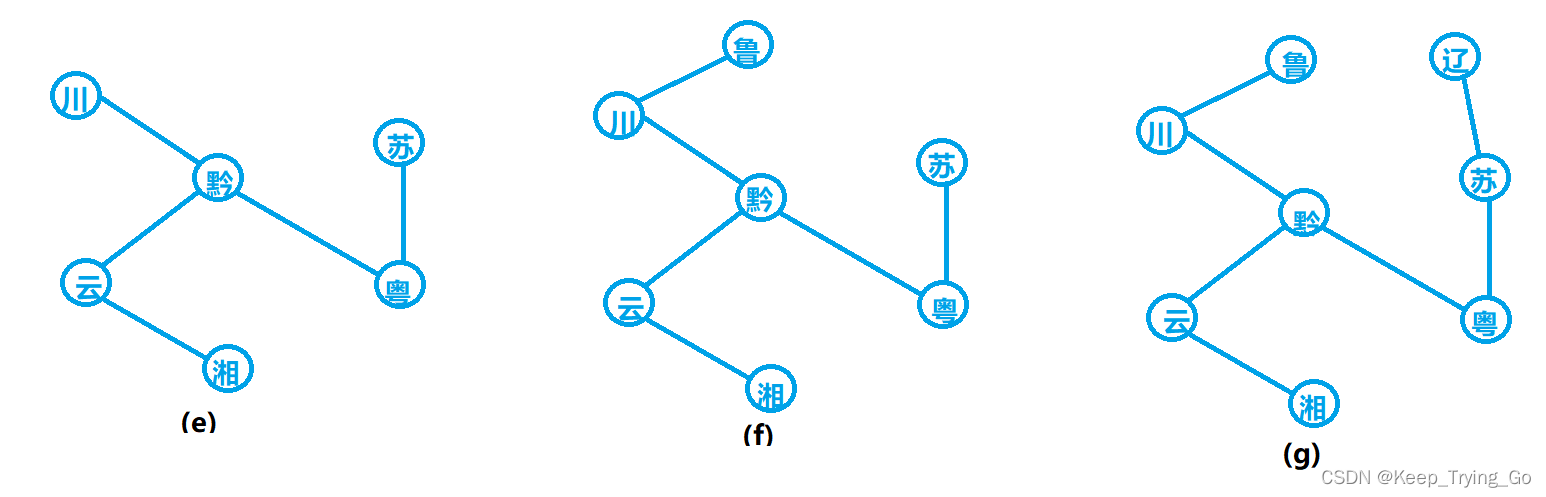
(1)Prim算法
思路:假设N=(V,{E})是连通网,TE是N上最小生成树中边的集合。算法从U={U0},TE={}开始,重复执行以下的操作:
在所有u∈U,v∈V-U的边(u,v)∈中找一条代价最小的边(u0,v0)并入集合,同时v0并入U,直至U=V为止。此时TE中必有n-1条边,则T={V,{TE}}为N的最小生成树。
直白的讲就是从集合只有u0顶点开始寻找与其边最短的顶点v0,这时集合中有顶点u0,v0,再从V-{u0,v0}的集合中继续找和集合{u0,v0}最短的边,直至集合{u0}->{u0,v0,……,vn}(所有的顶点选择完毕).
#include<stdlib.h>
#include<stdio.h>
#include<math.h>
#define inf 0x3f3f3f3f
#define maxx 505
int e[maxx][maxx];//记录两点之间的权值
int n,m;
int vis[maxx];//记录访问情况
int dist[maxx];//记录最短距离
int p[maxx];//记录前驱节点
int mincost;//记录最小费用
void Prim(int u){
for(int i=1;i<=n;i++){
dist[i]=e[u][i];
p[i]=u;
}
vis[u]=1;
dist[u]=0;
for(int i=1;i<=n;i++){
double temp=inf;
int t=u;
for(int j=1;j<=n;j++){
if(!vis[j]&&dist[j]<temp){
temp=dist[j];
t=j;
}
}
if(t==u)break;
vis[t]=1;
mincost+=dist[t];
for(int j=1;j<=n;j++){
if(!vis[j]&&dist[j]>e[t][j]){
dist[j]=e[t][j];
p[j]=t;
}
}
}
}
void displayEdge(int n){
for(int i=2;i<=n;i++){
printf("%d -> %d: %d\n",p[i],i,dist[i]);
}
}
int main(){
int t;
printf("请输入顶点数和边数: \n");
while(scanf("%d %d",&n,&m)){
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==j){
e[i][j]=0;
}else{
e[i][j]=inf;
}
}
}
for(int i=0;i<maxx;i++){
vis[i]=0;
p[i]=0;
dist[i]=inf;
}
for(int i=1;i<=m;i++){
int a,b,cost;
scanf("%d %d %d",&a,&b,&cost);
e[a][b]=e[b][a]=cost;
}
mincost=0;
Prim(1);
printf("最小费用 = %d\n",mincost);
displayEdge(n);
printf("请输入顶点数和边数: \n");
}
return 0;
}
/*
8 14
1 2 500
1 3 450
1 4 800
1 5 600
1 6 950
1 7 1100
1 8 1500
2 3 650
2 6 800
3 4 450
4 5 750
5 7 450
6 8 1000
7 8 900
*/

(2)Kruskal

//方法二:并查集模版
#include<stdio.h>
#include<math.h>
#define inf 0x3f3f3f3f
#define maxx 505
int pre[maxx];
int rank[maxx];
struct node{
int u,v;
int cost;
}e[maxx];
int cmp(node a,node b){
return a.cost<b.cost;
}
int mincost;
int n,m;
void init(){
for(int i=0;i<maxx;i++){
pre[i]=i;
rank[i]=0;
}
}
int find(int x){
int r=x;
if(pre[x]==r){
return x;
}
return pre[x]=find(pre[x]);
}
void unio(int x,int y){
int fx=find(x);
int fy=find(y);
if(rank[fx]<rank[fy]){
pre[fx]=fy;
}else{
pre[fy]=fx;
if(rank[fx]==rank[fy]){
rank[fx]++;
}
}
}
void Kruskal(int m){
mincost=0;
int cnt=0;
for(int i=1;i<=m;i++){
int x=find(e[i].u);
int y=find(e[i].v);
//如果不在一个集合中则可以合并
if(x!=y){
mincost+=e[i].cost;
unio(x,y);
cnt++;
}
if(cnt==n-1)break;
}
printf("最短路 = %d\n",mincost);
}
void sort(int n,int m){
for(int i=1;i<=m;i++){
for(int j=1;j<=m-i;j++){
if(cmp(e[j+1],e[j])){
node temp=e[j];
e[j]=e[j+1];
e[j+1]=temp;
}
}
}
}
int main(){
printf("请输入顶点数和边数: \n");
while(scanf("%d %d",&n,&m)!=EOF){
init();
for(int i=1;i<=m;i++){
scanf("%d %d %d",&e[i].u,&e[i].v,&e[i].cost);
}
sort(n,m);
Kruskal(m);
printf("请输入顶点数和边数: \n");
}
return 0;
} 从上面的Prim和Kruskal算法可以看到,Prim算法只跟顶点数有关,而Kruskal和边有关,所以对于稠密图Prim更加适合,而对于稀疏图Kruskal更加的适合。
本文含有隐藏内容,请 开通VIP 后查看