
题目为给定我们一个n的排列为p,让我们从1-n的序列中选出长度为k的子序列
满足任意
计算方案数,对998244353取模
首先我们可以对每一个i到p[i]连边
这样我们可以得到若干的环

比如前两个样例
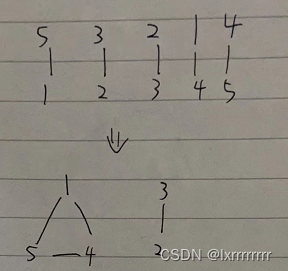
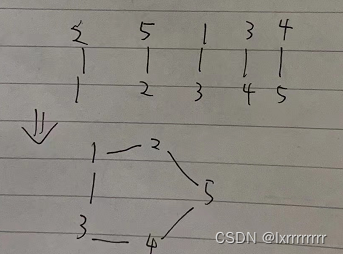
很明显依据题意,我们不能选择环上相邻的点
问题就转化为从数个环上选出k个点,使得所有点都不相邻
很明显是一道生成函数
我们计算每一个环的生成函数,使得
其中n是环上点的总数
表示从长度为n的环中选i个点的选法
这是一个环式不相邻问题
这里写一个简单的推倒
我们知道从n个点选m个不相邻的点的链式不相邻问题的答案是
而对于环式,我们可以选一个点或不选一个点
选一个点,旁边的两个点就不能选,就转化为一个从n-3个点中选m-1个不相邻的点,转化为链式
答案为
不选一个点,那么转化为一个从n-1个点选m个不相邻,转化为链式
答案为
所以环不相邻答案为
对不相邻问题困惑可以参考->(32条消息) 算法题(模板)——N个球放入M个盒子中_chicken3wings的博客-CSDN博客_将n个球放入m个盒子中
和
(32条消息) 不相邻问题_hht2005的博客-CSDN博客_环形不相邻问题
得到这个答案就可以先算出每个环的生成函数,然后分治合并,取最后答案的第k项就是答案
代码如下
#include <bits/stdc++.h>
#define int long long
#define fer(i,a,b) for(int i=a;i<=b;i++)
#define der(i,a,b) for(int i=a;i>=b;i--)
#define len(x) ((int)x.size())
#define pb push_back
#define mod 998244353
using namespace std;
template <typename _Tp>void input(_Tp &x){
char ch(getchar());bool f(false);while(!isdigit(ch))f|=ch==45,ch=getchar();
x=ch&15,ch=getchar();while(isdigit(ch))x=x*10+(ch&15),ch=getchar();
if(f)x=-x;
}
template <typename _Tp,typename... Args>void input(_Tp &t,Args &...args){input(t);input(args...);}
const int N=500050;
inline int add(int x, int y) {
x += y;
if(x >= mod) x -= mod;
return x;
}
inline int sub(int x, int y) {
x -= y;
if(x < 0) x += mod;
return x;
}
inline int mul(int x, int y) {
return 1ll * x * y % mod;
}
inline int qpow(int x, int y) {
int ret = 1;
for(; y; y >>= 1, x = mul(x, x)) if(y & 1) ret = mul(ret, x);
return ret;
}
const int G = 3;
const int Ginv = qpow(G, mod - 2);
int rev[N<<1];
inline void ntt(int *a, int n, int o) {
for(int i = 0; i < n; i ++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) * (n >> 1));
for(int i = 0; i < n; i ++) if(rev[i] > i) swap(a[i], a[rev[i]]);
for(int len = 2; len <= n; len <<= 1) {
int w0 = qpow((o == 1)? G : Ginv, (mod - 1) / len);
for(int j = 0; j < n; j += len) {
int wn = 1;
for(int k = j; k < j + (len >> 1); k ++, wn = mul(wn, w0)) {
int X = a[k], Y = mul(a[k + (len >> 1)], wn);
a[k] = add(X, Y), a[k + (len >> 1)] = sub(X, Y);
}
}
}
int ninv = qpow(n, mod - 2);
if(o == -1)
for(int i = 0; i < n; i ++) a[i] = mul(a[i], ninv);
}
#define clr(a, n) (memset(a, 0, sizeof(int) * n))
int aa[N << 1], bb[N << 1], lim=262144*4;
inline vector<int> operator * (const vector<int> & A, const vector<int> & B) {
for(int i = 0; i < len(A); i ++) aa[i] = A[i];
for(int i = 0; i < len(B); i ++) bb[i] = B[i];
vector<int> C;
C.resize(min(lim, len(A) + len(B) - 1));
int len = 1;
for(; len <= len(A) + len(B) - 1; len <<= 1);
ntt(aa, len, 1), ntt(bb, len, 1);
for(int i = 0; i < len; i ++) aa[i] = mul(aa[i], bb[i]);
ntt(aa, len, -1);
for(int i = 0; i < len(C); i ++) C[i] = aa[i];
clr(aa, len), clr(bb, len);
return C;
}
vector<int> Pi(int l,int r,const vector<vector<int>> &v){
if(l==r) return v[l];
int m=(l+r)>>1;
return Pi(l,m,v)*Pi(m+1,r,v);
}//卷积合并
int fc[N],gc[N];
inline void init(){
fc[0]=1;
for(int i=1;i<=500001;i++) fc[i]=mul(fc[i-1],i);
gc[500001]=qpow(fc[500001],mod-2);
for(int i=500001;i>=1;i--) gc[i-1]=mul(gc[i],i);
}
inline int C(int i,int j){
if(j>i)return 0;
return mul(mul(fc[i],gc[j]),gc[i-j]);
}//大组合数
inline int calu(int n,int m){
return add(C(n-m,m),C(n-m-1,m-1));
}//推出的式子
int p[N];
bool vis[N];
int n,k;
signed main(){
init();
int T;
input(T);
while(T--){
input(n,k);
fer(i,1,n){
input(p[i]);
vis[i]=0;
}
vector<int> cirsize;
vector<vector<int>> totcri;
fer(i,1,n){
if(vis[i]) continue;
int x=i;
int tmp=0;
do{
vis[x]=1;
x=p[x];
tmp++;
}while(!vis[x]);
cirsize.pb(tmp);
}//爆搜出所有环
for(auto nt:cirsize){
vector<int> A(nt/2+1);
A[0]=1;
for(int i=1;i<=nt/2;i++){
A[i]=calu(nt,i);
}
totcri.pb(A);
}//计算每个环的生成函数
vector<int> res=Pi(0,totcri.size()-1,totcri);//ntt合并
res.resize(n+1);
cout<<res[k]<<'\n';
}
return 0;
}
本文含有隐藏内容,请 开通VIP 后查看