端到端机器学习导航:
【机器学习】python借助pandas加载并显示csv数据文件,并绘制直方图
【机器学习】python使用matplotlib进行二维数据绘图并保存为png图片
【机器学习】python借助pandas及scikit-learn使用三种方法分割训练集及测试集
【机器学习】python借助pandas及matplotlib将输入数据可视化,并计算相关性
【机器学习】python机器学习借助scikit-learn进行数据预处理工作:缺失值填补,文本处理(一)
【机器学习】python机器学习scikit-learn和pandas进行Pipeline处理工作:归一化和标准化及自定义转换器(二)
【机器学习】python机器学习使用scikit-learn评估模型:基于普通抽样及分层抽样的k折交叉验证做模型选择
【机器学习】python机器学习使用scikit-learn对模型进行微调:使用GridSearchCV及RandomizedSearchCV
【机器学习】python机器学习使用scikit-learn对模型进行评估:使用t分布及z分布评估模型误差的95%置信空间
【机器学习】python机器学习使用scikit-learn对模型进行微调:RandomizedSearchCV的分布参数设置
【机器学习】python机器学习使用scikit-learn对模型进行微调:按特征贡献大小保留最重要k个特征的transform
【机器学习】python机器学习使用scikit-learn对模型进行微调:使用RandomizedSearchCV对pipline进行参数选择
RandomizedSearchCV基本操作
RandomizedSearchCV调参常用分布函数:
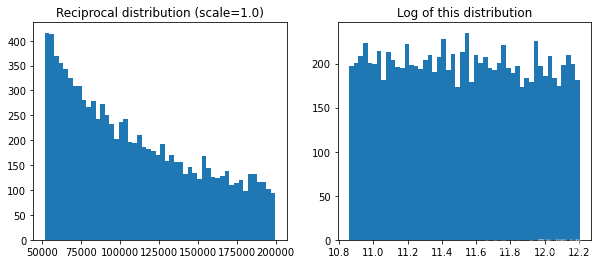
1.倒数分布:
import numpy as np
#这两个值决定了reciprocal返回的最大及最小值
reciprocal_distrib = reciprocal(52000, 200000)
samples = reciprocal_distrib.rvs(10000, random_state=42)
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.title("Reciprocal distribution (scale=1.0)")
#直方图,一种特殊的柱状图。
#将统计值的范围分段,即将整个值的范围分成一系列间隔,然后计算每个间隔中有
#多少值。
plt.hist(samples, bins=50)
plt.subplot(122)
plt.title("Log of this distribution")
# 取对数之后不会改变数据的性质和相关关系,但压缩了变量的尺度
#右图可以看出倒数分布较为均匀,可以用于不知道具体值的情况
plt.hist(np.log(samples), bins=50)
plt.show()
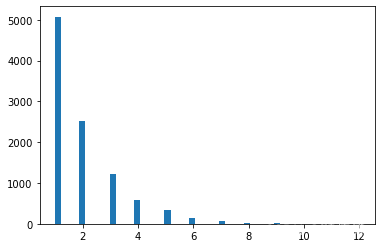
2.几何的离散分布及指数分布
from scipy.stats import geom, expon
#几何离散分布,大部分取值范围是0到8左右
geom_distrib=geom(0.5).rvs(10000, random_state=42)
#连续分布,scale=1时,大部分取值范围是0.1到7.5左右
expon_distrib=expon(scale=1).rvs(10000, random_state=42)
plt.hist(geom_distrib, bins=50)
plt.show()
plt.hist(expon_distrib, bins=50)
plt.show()
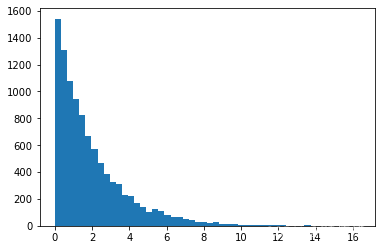
综上,最优参数取值较为确定时,使用geom或expon,不确定时使用reciprocal。
例子:
进行数据准备:
import os
HOUSING_PATH = os.path.join("datasets", "housing")
import pandas as pd
def load_housing_data(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
housing=load_housing_data()
housing2=housing.copy()
import numpy as np
#预处理前去掉带文字的指定列
from sklearn.preprocessing import MinMaxScaler,StandardScaler,OneHotEncoder
from sklearn.impute import SimpleImputer
housing_num = housing2.drop("ocean_proximity", axis=1)
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
num_pipeline = Pipeline([
('imputer', SimpleImputer(strategy="median")),
('std_scaler', StandardScaler())
])
from sklearn.compose import ColumnTransformer
#返回所有列名
num_attribs = list(housing_num)
cat_attribs = ["ocean_proximity"]
#找出待独热编码列的最大分类数,不然在进行测试集划分处理时,
#容易造成独热向量因测试集构成不同而列数不一致的情况
categories=housing2['ocean_proximity'].unique()
full_pipeline = ColumnTransformer([
("num", num_pipeline, num_attribs),
("cat", OneHotEncoder(categories=[categories]), cat_attribs),
])
#抽样后的数据,去除预测目标列,并拿出对应目标列准备数据训练
housing_labels = housing2["median_house_value"]
housing_prepared = full_pipeline.fit_transform(housing2)
from sklearn.model_selection import train_test_split
train_set, test_set,train_sety, test_sety = train_test_split(housing_prepared,housing_labels, test_size=0.1, random_state=42)
进行随机搜索:
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import randint
from scipy.stats import expon, reciprocal
from sklearn.svm import SVR
import matplotlib.pyplot as plt
import numpy as np
reciprocal_distrib = reciprocal(52000, 200000)
from scipy.stats import geom, expon
geom_distrib=geom(0.5).rvs(10, random_state=42)
print(geom_distrib)
param_distribs = {
#对于搜索范围是list的超参数,在给定的list中等概率采样
'kernel': ['linear', 'rbf'],
'C': reciprocal(20, 200),
'gamma': expon(scale=1.0),
}
svm_reg = SVR()
rnd_search = RandomizedSearchCV(svm_reg, param_distributions=param_distribs,
n_iter=2, cv=2, scoring='neg_mean_squared_error',
verbose=2, random_state=42)
rnd_search.fit(train_set[:1000], train_sety[:1000])
#均方根误
negative_mse = rnd_search.best_score_
rmse = np.sqrt(-negative_mse)
rmse
#最优参数
rnd_search.best_params_
输出结果为:
[1 5 2 2 1 1 1 3 2 2]
Fitting 2 folds for each of 2 candidates, totalling 4 fits
[CV] END C=47.37727900728156, gamma=3.010121430917521, kernel=linear; total time= 0.0s
[CV] END C=47.37727900728156, gamma=3.010121430917521, kernel=linear; total time= 0.0s
[CV] END C=120.42620370295205, gamma=0.9084469696321253, kernel=rbf; total time= 0.0s
[CV] END C=120.42620370295205, gamma=0.9084469696321253, kernel=rbf; total time= 0.0s
#最优参数
{'C': 47.37727900728156, 'gamma': 3.010121430917521, 'kernel': 'linear'}