DFA 又称为有穷自动机,在编译器词法分析器,硬件设计,游戏AI逻辑中有着广泛的应用。
DFA和NFA 的描述能力是等价的,NFA便于人们理解和记忆,NFA可以通过子集法转换成DFA,但是状态集不是最小化的。下面给出DFA最小化状态集自动化简的算法,Flex中有实现的源代码。
具体说明和证明过程、算法示例如下
首先,正规式,正规集,DFA,NFA,以及正规文法,从自动机识别或者正规文法生成角度讲,都是等价的,具体的证明过程,可以参考形式语言与自动机理论中的详细证明过程,即 L(M) = G(M')。
即两个字母表 ∑a 和 字母表 ∑b 的连接之后,指定具体的产生式规则,所生成的语言G,和通过构造DFA,产生的自动机识别的语言集合 L 是等价的。
基于此,咱们再来看下DFA 化简算法的具体算法过程。
由于对能识别两个字符集的所有自动机M可以通过 (|,*,·)三种运算(正则的定义)扩充,题主这里只是其中一种连接运算,因此可以通过连接合并成一个大的自动机M‘,这个自动机能够识别所有的字母表中的字。
于是问题转化为对DFA M’,使得M‘的状态最少,转化为:
寻找一个状态数比M' 少的DFA M'',使得L(M') = L(M'')
先得给出两个定义,假设s和t为M‘的两个状态,称s和t等价 等价:
当且仅当 对于任意的状态s,如果从状态s出发能读出某个字a而停止于终态,那么同样,从t出发也能读出a而停止于终态;反之亦然。
如果两个状态不等价,则称是 可区别 的,这个定义再用数学语言描述一下:
存在一个字a,要么s读出a停止于终态而t读出a停止于非终态,要么t读出a停止于终态而s读出a停止于非终态。
这个稍微解释一下,就是说如果要判定DFA状态机中的任意两个状态是否等价,需要根据状态机中的任意两个状态s和t,指定相同的输入符号(字)a,其跳转到的终态是一致的,才能判定s和t是等价的,否则不是等价状态,其中为何是指定单个字,这个是DFA的定义,当然需要考虑空串 ε。
因此问题本质上是状态机DFA M‘的等价类划分的问题。
DFA M‘最少化的基本思想:
把M的状态集划分为一些不相交的子集,使得任何两个不同子集的状态是可以区别的,而同一子集的任何两个状态是等价的。最后,让每个子集选出一个代表,同时消去其他相同状态。
按照这个基本思想,对任意的一个DFA M‘进行第一次划分,需要根据 终态和非终态来进行选取。
为什么不根据初态和非初态来划分,这里是因为第一次划分之后,需要保证任何两个不同子集的状态是可以区别的,而根据DFA的定义来看,只有终态在输入 ε 后还能保持在终态,因此需要根据终态来进行划分,接下来就可以递归来处理了。
对DFA M‘的状态集合S进行划分的细节算法:
1.首先,把S划分为终态和非终态两个子集,形成基本的划分 π
2.假定到某个时候, π 已包含m个子集,记为 π={l1,l2,...,lm}
检查 π 中的每个子集看是否能进一步划分:
步骤a.
对于 li ,令 li={s1,s2,...,sk} ,若存在一个输入字符a使得 lai (即当前的可区别的子集,输入a字符的条件下) 不会包含在现行 π 的某个子集 lj 中(因为相同的子集是等价的,这个是反推),则至少应把 li 分为两个部分。
具体的推导如下(见图1):
1) 假定状态s1和s2经a弧分别到达t1和t2
2) t1和t2属于现在 π 中的两个不同子集(题设是可区别的)
2.1) 说明有一个字a,t1读出a后到达终态,而t2读出a后不能达到终态,或者反之
3)那么对于字a α ,s1读出a α之后到达终态,而s2读出a α不能到达终态,或者反之
4)因此s1和s2不等价
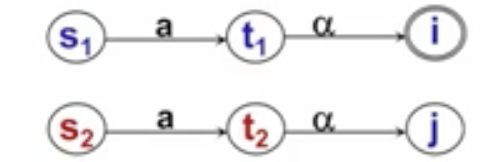
图1
步骤b.
递归过程:将 li 分成两个部分,使得一半包含状态s1:
且经弧到达,且与属于现行中的同一子集li1={s|s∈li且s经a弧到达t,且t与t1属于现行π中的同一子集}
剩余的另外一部分则为
li2=li−li1
一般地,对于某个a和 li ,若 lai 属于 π 中N个不同子集,则应把 li 划分成N个不相交的组,使得每个组J的 Ja 都属于 π 的同一个子集,这样构成新的划分。
步骤c.
重复上述过程,直到 π 所含子集数不再增长。
步骤d.
对于上述最后划分 π 中的每个子集,我们选取每个子集I中的一个状态代表其他状态,则可得到化简后的DFA M‘’
若I含有原来的初态,则其代表的新状态为新的初态,
若I含有原来的终态,则其代表的新终态为新的终态。
说明:
由于有限状态机的状态是有限的,算法一定能停止。
用某教科书上的案例,举个例子(采用上述算法自动化简如下DFA):
编辑切换为居中
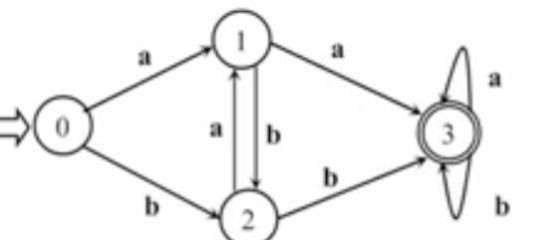
图2 需要最小化状态集的DFA
第一步是按照终态和非终态划分成两个集合,如图3,后面有下标的表示输入的字符a或者b
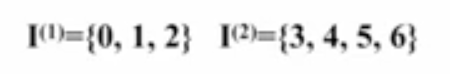
编辑
图3 第一次划分
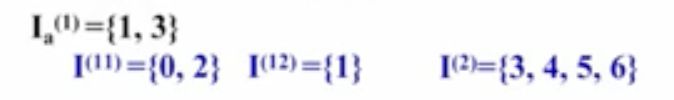
编辑切换为居中
图4 第二次划分,第一个集合输入a,蓝色左边两个表示黑色集合的一次划分
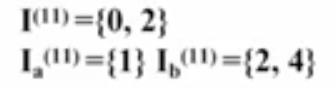
编辑
图5 深度遍历进行第三次划分
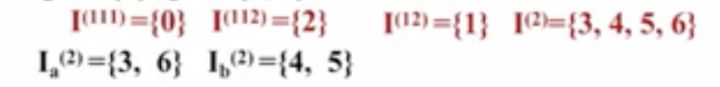
编辑切换为居中
图6 第四次划分,重复直到划分后的集合不再随着输入弧字符变化
编辑
图7 最后采用算法化简后的最小化状态集DFA
2