目录

1：深搜

2：广搜

1：深搜

（1）定义

深度搜索，按照一条路如果可以走的话一直走下去，相当于不撞南墙不回头

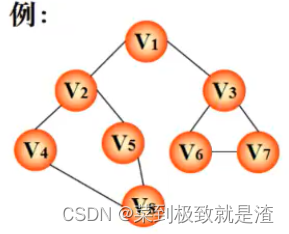
 比如如上图，深搜的话有：

v1--v2--v4--v8

v1--v2--v5--v8

v1--v3--v6

v1--v3--v7

我们做个典型的题目来理解下（大家点击下全排列就可以到达题目的网页了）：全排列

 读了题目我们对于题目的理解是，输入一个数n，从一到n，然后开始全排列。以前我们是一个一个的列出，就是谁用过了，后面我们就不用了（这个标记下就行），直到所有的情况都被列举出来。接下来我们看下代码哈

#include<bits/stdc++.h>
using namespace std;
int n;
bool v[20];//判断数i是否使用过
int a[20];//将列举的数存进去
void dfs(int ans)//ans表示现在已经排好了多少个数
{
	if(ans>n){
		for(int i=1;i<=n;i++){
			cout<<setw(5)<<a[i];
		}
		cout<<endl;
		return ;
	}
	for(int i=1;i<=n;i++){
		if(!v[i]){
			//如果该数没有使用过
			a[ans]=i;
			v[i]=true;
			dfs(ans+1);//继续深搜下去
			v[i]=false;//复原，用作下一次的深搜
		}
	}
}
int main()
{
	cin>>n;
	dfs(1);
	return 0;
}

2：广搜：

（1）定义：广搜的意思就是同时走多种路径，层层搜索，往往用作是最优解，用队列来解决

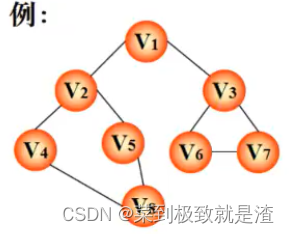
广搜：v1--v2--v3--v4--v5--v6--v7--v8 

同样的我们来做个题目理解下（点击马的遍历即可）马的遍历

读了题目后，我们知道了大概的题意就是输出一匹马在起始点后走到棋盘中各个点需要的步数（这里的步数就是移动的次数），无法到达则为-1。这题用深搜肯定也是行的，但是不是时间复杂度太大了啊，所有我们用广搜，层层递进。接下来，我们看下代码。 

#include<bits/stdc++.h>
using namespace std;
int n,m,x,y;
int xx[]={-2,-2,-1,-1,1,1,2,2};
int yy[]={-1,1,-2,2,2,-2,-1,1};
int ma[500][500];//地图
bool v[500][500];
typedef struct{
	int a,b;//坐标
	int step;//步数
}node;
queue<node>q;
int main()
{
	ios::sync_with_stdio(false);//快读，理解成死记硬背的知识就行啦，固定格式蛮
	cin>>n>>m>>x>>y;
	memset(ma,-1,sizeof(ma));//将地图全部初始化为-1
	ma[x][y]=0;//起始点需要的步数是0
	v[x][y]=true;//起始点已经访问过
	node k,u;
	k.a=x;
	k.b=y;
	k.step=0;
	q.push(k);
	while(!q.empty()){
		u=q.front();
		q.pop();
		for(int i=0;i<8;i++){
			int dx=xx[i]+u.a;
			int dy=yy[i]+u.b;
			if(dx>=1&&dx<=n&&dy>=1&&dy<=m&&v[dx][dy]==false){//满足在这个棋盘上并且没有走过的条件
				v[dx][dy]=true;
				node f;
				f.a=dx;
				f.b=dy;
				f.step=u.step+1;
				ma[dx][dy]=f.step;
				q.push(f);
			}
		}
	}
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cout<<setw(5)<<left<<ma[i][j];
		}
		cout<<endl;
	}
	return 0;
}

 好啦，本篇关于搜索的文章就此结束啦，搜索无止境，学习无止境，大家多练习啊！！！！