
今天我们主要讲一下多重同步压缩变换multisynchrosqueezing transform(MSST)在信号处理中的应用.
原文:Yu G , Wang Z , Zhao P . Multisynchrosqueezing Transform[J]. Industrial Electronics, IEEE Transactions on, 2018.
前置文章:
同步压缩变换初探 - 哥廷根数学学派的文章 - 知乎 同步压缩变换初探 - 知乎
高阶同步压缩变换--占坑 - 哥廷根数学学派的文章 - 知乎 高阶同步压缩变换--占坑 - 知乎
同步挤压小波变换-尺度转换为频率 - 哥廷根数学学派的文章 - 知乎 同步挤压小波变换-尺度转换为频率 - 知乎
改进多重同步压缩变换improved multisynchrosqueezing transform(IMSST)在信号处理中的应用 - 哥廷根数学学派的文章 - 知乎 改进多重同步压缩变换improved multisynchrosqueezing transform(IMSST)在信号处理中的应用 - 知乎
多重同步压缩变换 (MSST)通过迭代重分配技术对信号的时频分量能量分布进行多次同步压缩变换SST以提高非稳态信号时频分布中特征信号分量的能量集中度。
先简要看一下SST原理

MSST是在SST基础上通过多次迭代使得信号时频分量的能量在其瞬时频率附近得到进一步压缩,以获得能量高度集中的时频分布。多重同步压缩变换表达式为:

通过多次迭代,由式(4)表述的瞬时频率将会越来越接近信号的真实瞬时频率,从而获得强时变信号的高分辨率时频谱图。
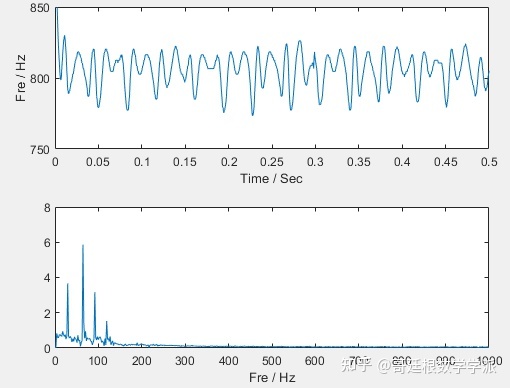
首先,先导入一个实际的机械振动信号
load('vib_data1.mat')
fs = 12000; %采样频率
N = 1200; % 采样点数
time = (1:N)/fs; % 时间序列
fre = (fs/2)/(N/2):(fs/2)/(N/2):(fs/2); %频率序列
data=data(1:N);看一下时域图和频谱图
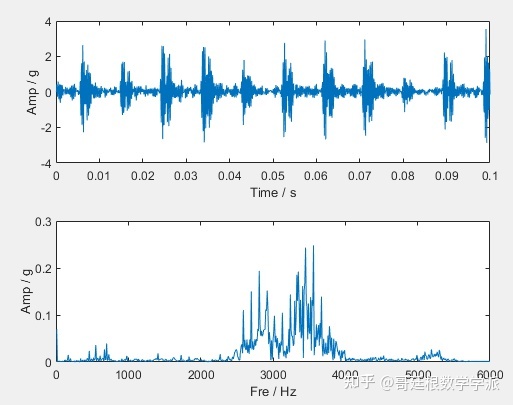
看一下信号的STFT时频谱图
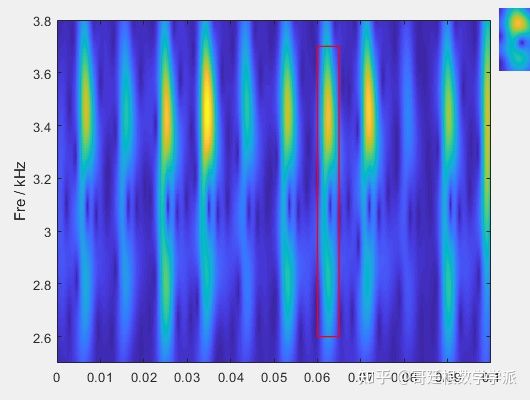
然后看一下标准的同步压缩变换,即SST时频谱图(基于短时傅里叶变换STFT)
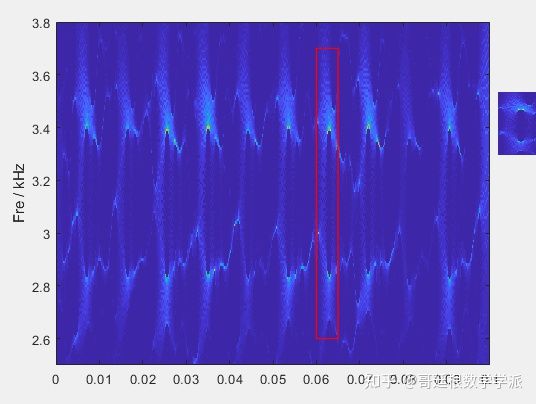
竖直2阶同步压缩变换时频谱如下(以后会讲,包括水平同步压缩变换)
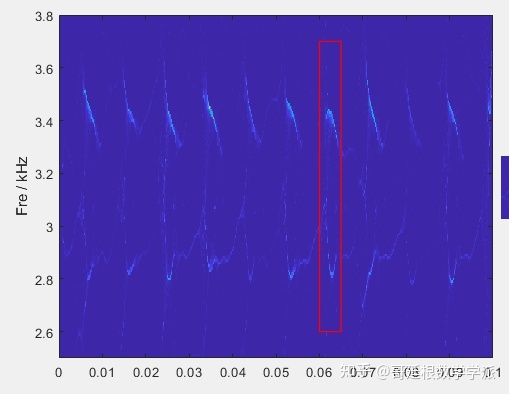
竖直4阶同步压缩变换时频谱如下(以后会讲)
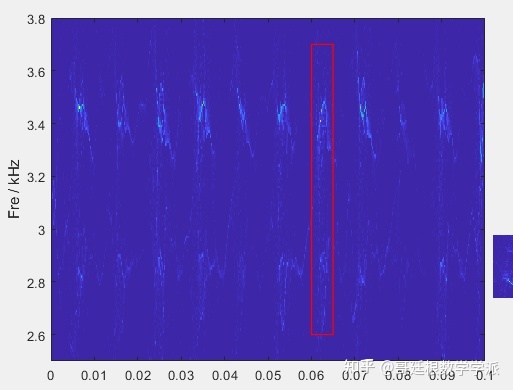
MSST时频谱图如下

顺便看下MSST提取的两条时频脊线
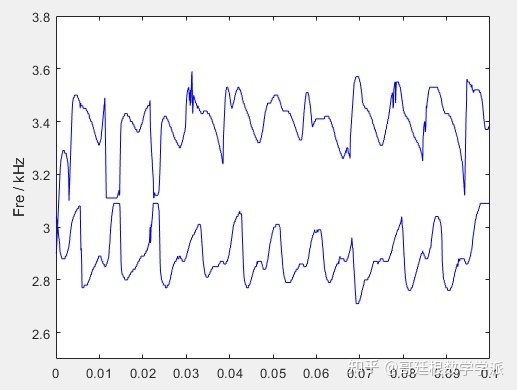
两条时频脊线所对应的两个分解分量
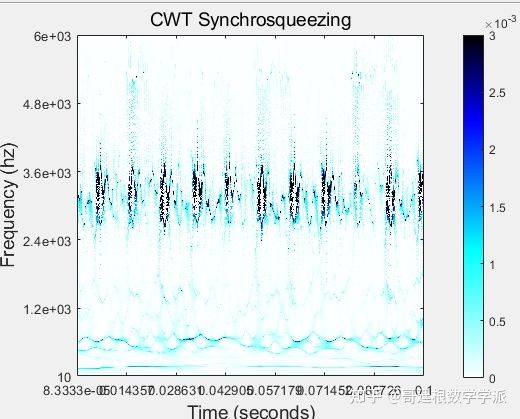
看下连续小波变换CWT时频谱图
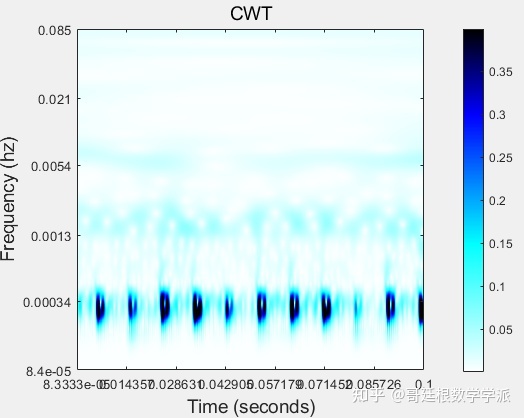
同步压缩小波变换的时频谱,下次试试高阶同步压缩小波变换,效果应该会不错
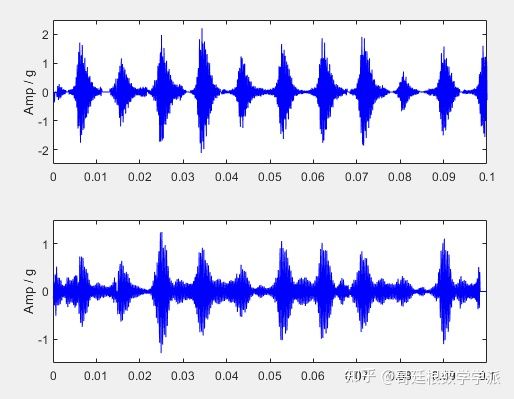
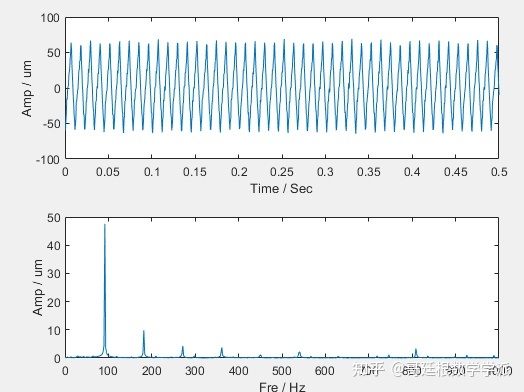
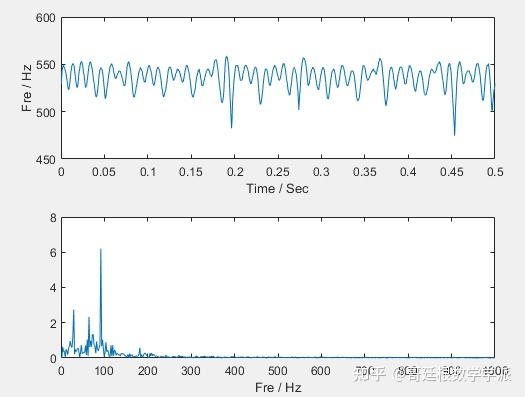
然后再看一组转子振动数据,其时域波形和频谱如下
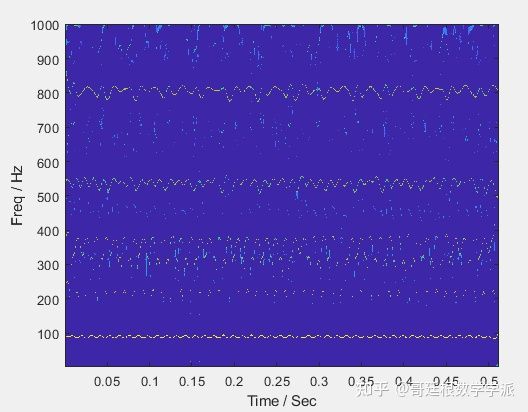
其MSST时频谱如下
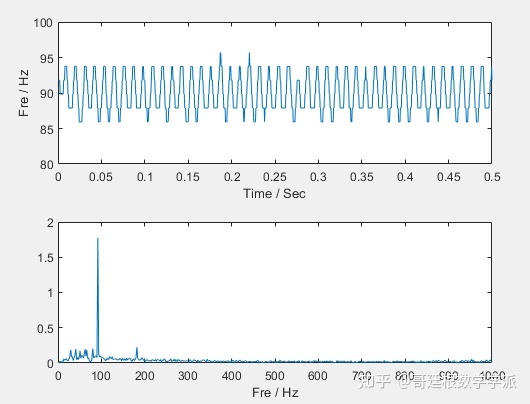
根据上面的MSST时频谱图,可以得到主要的3个分量
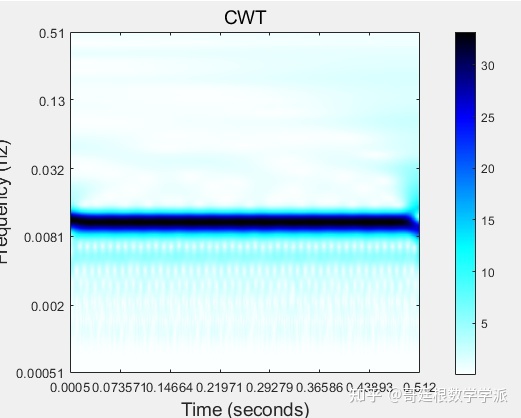
看一下连续小波变换的CWT时频谱图
其同步压缩小波变换时频谱图如下
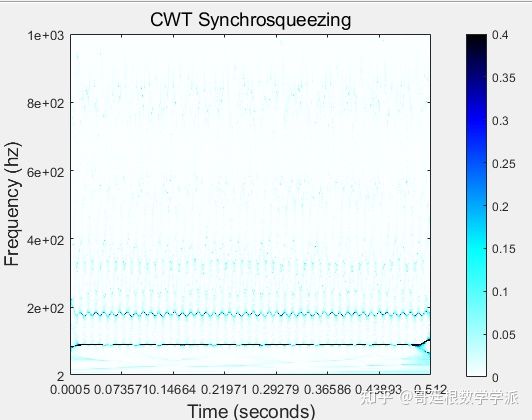
放大一下
详细文章也可见
多重同步压缩变换multisynchrosqueezing transform(MSST)在信号处理中的应用 - 哥廷根数学学派的文章 - 知乎
https://zhuanlan.zhihu.com/p/553410298