笔记来源于：3B1B：散度与旋度：麦克斯韦方程组、流体等所用到的语言

向量分析的两个核心思想：散度和旋度

1.向量场（Vector Fields）

向量场就是把空间上的每个点赋予一个向量，使它带有长度和方向
（颜色代表大小程度）

1.1 流场

这些向量可以代表流体粒子在每一点的速度

绝大多数流体随时间而发生改变

1.2 引力场

这些向量也可以表示空间不同位置的引力大小

1.3 磁场

这些向量也可以表示每个点的磁场强度

1.4 电场

随着电荷的移动，电场也在发生改变

假设所有向量代表某种流体在平面各点的流速

1.5 二维向量场函数

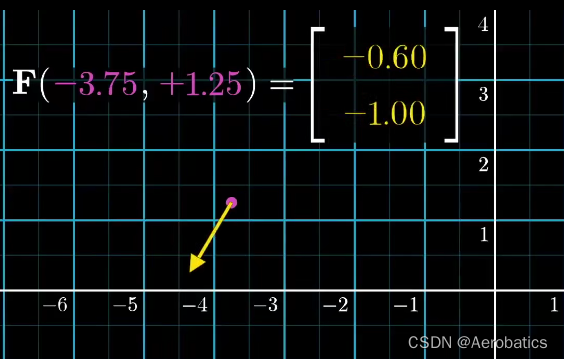
2.散度（Divergence）

散度是描述空气从周围汇合到某一处或从某一处流散开来程度的量
散度的值表示：在该点处散发出来的流体的量是多少

某点邻域中，流体流向此点或流出此点的量的多少

2.1 散度的含义

向量场在平面上某一点的散度告诉你，此点向外【发射】或向内【吸收】“流体”的量是多少

2.2 散度大于0的情况

散度$>0$ 向外“发射”流体多于向内“吸收的流体，总体效果为向外“发射””
说明该点像个泉眼（数学上叫“源”）

散度$>0$ 向外流出的流体流速快于向内流入的流体流速

2.3 散度小于0的情况

散度$<0$ 向内“吸收”的流体多于向外“发射”流体，总体效果为向内“吸收”流体
说明该点像个下水道（数学上叫“汇”）

2.4 向量场的散度

以二维平面内某点作为输入，但其输出是受该点邻域所影响的，而输出的就是衡量此点所表现出的“发射”或“吸收”量的一个数

如果流体不可压缩，则其速度向量场必然处处散度为0（某点附近流入和流出的流体量相同）

3.旋度（Curl）

3.1 旋度的含义

旋度是向量分析中的一个向量算子，可以表示三维向量场对某一点附近的微元造成的旋转程度。 这个向量提供了向量场在这一点的旋转性质

真正旋度的定义应该是三维的，此篇重点介绍二维

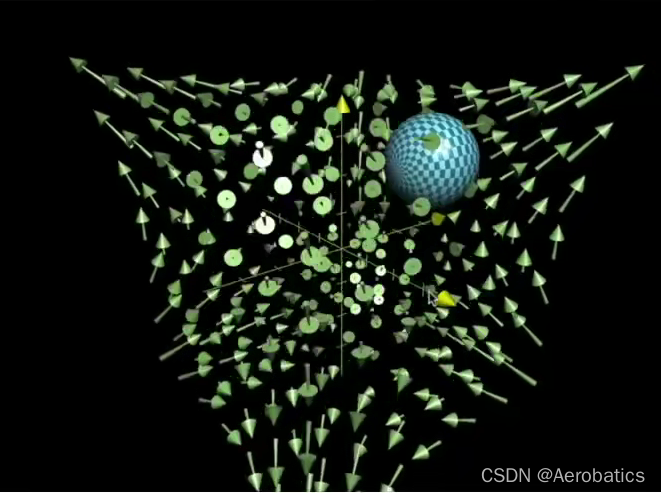
流体绕着这一点旋转的趋势大小

3.2 旋度大于0的情况

某点附近的向量逆时针旋转，则旋度大于0

3.3 旋度小于0的情况

某点附近的向量顺时针旋转，则旋度小于于0

某点附近上方流速快于下方，则此点旋度小于0

3.4 向量场的旋度

旋度大小：二维平面内一个点与一个数值结合

4.麦克斯韦方程组

描述电场和磁场的四个特殊方程（使用散度和旋度表示）

4.1 高斯定律

4.2 高斯磁定律

空间中磁场的散度处处为0

如果将磁场对应为某种流体的流动，那么这种流体应该是不可压缩的，因而空间不存在“源”也不存在“汇”（就像水一样），这里隐含了另外一个事实就是【磁单极子】单独存在磁铁北极或磁铁南极，事实上这是不存在的

4.2 法拉第感应定律、麦克斯韦-安培定律

一个场的变化如何依赖另一个场的旋度
这是一个纯粹的三维空间概念，这种散度和旋度的概念出现在无关流动的情形下

这两个方程的后退和前进正是光波产生的基础

5.一个实际问题

定义在某点的向量可以告诉你一组种群数量将向哪个方向并且以多快的速度变化
这个向量场是包含两个变量的动态系统以及这个动态系统随时间如何演化


此方法可以让我们知道对于初始状态系统将会如何演化，而散度和旋度可以帮助我们理解这个系统，比如流场收敛于哪些点？发散于哪些点？此例中种群数量会收敛于哪个值？循环在哪里？此循环是否稳定？
除了散度和旋度这两个数学工具外，你可能还会用到雅可比行列式