必做题整理与 Q&A

- 时间 2021年4月11日，时间21点40分，考完试十分怀疑人生，本来想靠专业课拉点分，也预料到今年专插本报名人数多，加上改革专业课应该会简单点，但是没想到啊，没想到，题目简单的实在不需要思考，处了考基础就是考基础，感觉靠专业课拉分是没什么希望了，不过还是把我自己手敲的资料发出来吧，这是我整理了历年专插本考试的试题，以为怎么也能考上个5题，结果一题没考上，连个排序都没到到，可能明年会增加难度吧，如果有需要的可以收藏一下
- 我还做了超详细的政治思维导图，我会把历年试题资料还有自己的笔记，都一并上传到CSDN，没有会员的可以私信发QQ邮箱给我，我邮箱发过去做个顺水人情，不过别忘记三连支持一下哦

• 资料链接🔗：本人已于2021年上岸，资料已经是2021年的，虽然插本考察的东西万年万年不变，但是最近繁忙，可能无法再一个个通过邮件的形式将资料发送给你们了，我尝试减小下载所需的硬币数，但是大部分资料都已经被我做成了文档，你可以通过在我的发布的文档直接在线阅读
  • 我考的还可以接受，2b学校应该是能让我随意选了，毕竟也就准备了八十来天，时间不长，成绩我也欣然接受，我自己建立的政治思维导图方式学习真的很不错，政治思维导图收录了考试的关键点，和视屏课的重点，以至于我看到选项就知道题目要问的是哪一块的内容，和答题的坑我都有记录在政治思维导图里面，由于视频的版权问题，我就只提供我个人收集和公开的资料啦
    另外，我已经把C语言和数据结构的笔记写成博客，如果你能看懂我这片博客全部内容，专业课170分应该是没有问题的，都是我按照历年真题最高标准准备的，博文的最后收录了19年前可能会考到的大题，大题预测我都有代码实现很值得看，可惜今年专业课太简单，19年五分之一的难度都没有，但我是按最高难度准备的，不知道今年难度会不会回升，估计回升太多的情况不大，所以认真学好C语言估计能拿140分，希望对你们有帮助，不要忘记一键三连支持一下👍🏻👍🏻👍🏻
  • 如果觉得不错的话可以给我的其他文章也点点收藏和赞支持一下，ps：这不是客套话，是真的去帮我点点赞和收藏吧，差不多可以给我十来个文章点吧，系统也有限制，好让系统对我的文章有更多推送，谢谢😏
    反正对你也没坏处，就当礼尚往来吧😉
• 近期也收到不少朋友问学习规划学习方法之类的问题，我这里做一个重新的编写吧，还有问题可以给我发私信或给我发邮件，haoyunlwh@qq.com，我用邮件回复你，有什么问题也能直接点回复跟我交流
• 学习规划，我是考试前4个月开始准备的，也没什么方法，正儿八经学的时间可能也就100天吧，以前有点编程基础，今年分数也满分两百，所以C语言和数据结构这方面花了2个月复习，政治也就花了二十来天，其余两科我是直接放弃的，那两科加起来不到50分，我总分285，175的专业课，也算是比较适合我这个咸鱼的战术了，毕竟确实不像话个一两年去准备插本考试，其他人还是不建议偏科，学习计划就是这样
• 学习方法最直接的就是看视频，刷题，反馈总结复盘答案，前两点很好理解，反馈总结复盘我觉得是最重要的，因为一种类型的题，通过会做到不会做，都是先直接看一遍答案 或 做一遍再看答案，我比较倾向的就是对于没做过的提醒直接看一次答案，学习答题思路，然后对答案进行分析，这一个类型的题目应该从什么角度答题，应该答几点，比较能提现的地方就是政治考试吧，简答题我按照思维导图的形式，将一个类型的问题拆分成几点来进行关联背题，背概括，不背一字不差，如果是四点的话，我可能拆分成四个短句，然后答题的时候加入一些熟读的话术来填充，比较建议就是直接读出来，概括，最好就制作思维导图，或者看我的思维导图，还有做笔记的弊端是容易给自己造成自己学进去了的假象，时不时要复习一下自己的笔记，尝试口述回答，光把笔记做的漂漂亮亮容易感动自己，这是真的，做笔记多思考，加入自己的总结，比较建议的是用电脑做笔记了，不容易乱，也好搜索内容，然后是专业课学习，按照改革后的考试分析，专业课的难度是大幅下降的，如果无基础建议从MOOC的基础课程开始学起，然后过一遍书，然后就开始刷题，刷题方面，我有在微信小程序买会员，在里面刷题，政治也在里面刷，100块，割韭菜就割一下吧，我觉得比报名34千的培训班我觉得划算点，因为我还是比较穷的，有钱还是建议直接培训班，然后在百度文库或CSDN找C语言的题来刷，做完题复盘答案，这点很重要，为什么错，哪一点容易被坑，C语言的题目和数据结构的题目在考试分布可能就是9：1吧，数据结构刷不刷题都无所谓，今年C语言的题出现的一种解释名词的题目，比如解释“什么是局部变量”占分也不小需要注意一下，大概24分左右，就这样吧
• 觉得有帮助可以给我其他文章也收藏点赞支持一下，反正对你也没坏处，就当礼尚往来吧😉

必做题整理

连接两个字符串

• char* Strcat(char* str1, const char* str2) {	int n = strlen(str1);	int i = 0;	while (str1++[i + n] = str2++[i]);	return str1;}char* Strcat(char* str1,char* str2) {	char * p1= str1,*p2 = str2;	int len1 = 0,len2 = 0;	if(str1==NULL){		return  str2;			}	if(str2 ==NULL){		return str1;			}	while (*p1++!='\0') {		len1++;			}	while (*p2++!='\0') {		len2++;	}	char * str3 = malloc(sizeof(char)*(len1+len2));	int i=0;		for (p1 = str1;*p1!='\0';p1++) {		*(str3+i) = *p1;		i++;					}	for (p2 = str2;*p2!='\0';p2++) {		*(str3+i) = *p2;		i++;			}	*(str3+i) ='\0';	return str3;}
  

素数

• sqrt   筛选法
  

水仙花数

• void daffodilNum(){	int x,y,z;		for (int i = 100;i<1000;i++) {		x = i/100;		y = i/10%10;		z = i%10;		if(i == x*x*x + y*y*y + z*z*z){			printf("%4d",i);					}		}}
  

所有排序

选择

• #define swap(A,B) int temp=A;A =B;B=temp;void selectSort1(int array[],int length){	for (int i=0;i<length;i++) {		int min =i;				for (int j = i;j<length;j++) {			if(array[min]>array[j]){				min = j;			}		}		swap(array[min], array[i]);			}}
  

插入

• void InsertSort2(int array[],int length){	int j ;	for (int i = 1;i<length;i++) {		int k = array[i];		for (j = i;j>0 && k<array[j-1] ;j--) {			array [j] = array[j-1];		}		array [j] = k;	}}
  

冒泡

• void bubbleSort(int array[],int length){	for (int i=1;i<length;i++) {		for (int j=i;j>0;j--) {			if(array[j]<array[j-1]){				swap(array[j], array[j-1]);			}		}	}}
  

shell

• void shellSort(int array[],int lenght){	for (int shell = lenght/2;shell>0;shell/=2) {		for (int i = shell;i<lenght;i++) {			if (array[i-shell]>array[i]) {				swap(array[i-shell],array[i]);			}		}	}}
  

归并

• void mergeab(int array[],int left,int right){	int i = left;	int mid = (left+right)/2;	int j = mid +1;	int k=left;		while ((i<=mid)&&(j<=right)) {		if(array[i]<array[j]){			b[k++] = array[i++];								}else {			b[k++] = array[j++];					}			}	if(i>mid){		for (i=j;i<=right;i++) {			b[k++] = array[i];					}		//j 段未完成			}else {		for (;i<=mid;i++) {			b[k++] = array[i];		}		// i 段未完成	}}void copy(int a[],int b[],int left,int right){	for (int i =left;i<=right;i++) {		a [i] = b[i];	}}void mergeSort(int array[],int left,int right){	int m = (left +right)/2;		if(right<= left){		return;			}	mergeSort(array,left,m);	mergeSort(array,m+1,right);	mergeab(array, left, right);		copy(array,b,left,right);}	
  

快速

• //partitionint partition(int array[],int left,int rigth){	int i=left ,j = rigth+1;	int standarn = array[left];	while (1) {		while (standarn>array[++i]) {			if(i==rigth){				break;							}		}		while (standarn<array[--j]) {			}		if(i>=j){			break;					}		swap(array[i], array[j]);					}	swap(array[j], array[left]);	return j;}int randomi (int minIndex,int maxIndex){	return minIndex+(maxIndex-minIndex)*(1.0*rand()/RAND_MAX);	}int randomPartition(int array[],int minIndex,int maxIndex){	int i = randomi(minIndex,maxIndex);	swap(array[i], array[i]);	return partition(array, minIndex, maxIndex);	}//quicksortvoid quickSort(int array[],int minIndex,int maxIndex){	if(minIndex>maxIndex)return;	int standarn  = randomPartition(array, minIndex, maxIndex);	quickSort(array, minIndex, standarn-1);	quickSort(array, standarn+1, maxIndex);	}
  

基数

• #define radix  10void RadixSort(int array[],int length){	int pow=1,max =-1;	int * temp_array=(int *) malloc(sizeof(int )*length);	for (int i=0;i<length;i++) {		if(max< array[i]){			max= array[i];		}	}	while (max/pow) {		int count[radix]={0};		for (int i=0;i<length;i++) {			++count [array[i]/pow%radix];					}		for (int i=1;i<radix;i++) {			count[i] += count[i-1];					}		for (int i=length-1;i>=0;i--) {			temp_array[--count[array[i]/pow%radix]] = array[i];					}		for (int i=0;i<length;i++) {			array [i]= temp_array[i];		}		pow *=radix;			}	free(temp_array);	}
  

数逆序

• void intarrayReverse(int array[],int length){	for (int i=0;i<length/2;i++) {		int temp = array[i];		array[i] = array[length-1-i];		array[length-1-i] = temp;	}}//正负数reverse反转int reverse(int n){	int sign=1,m;	if(n<0){		sign =-1;	}	n = (n>=0?n:-n);	m=n%10;	while (n>=10) {		n = n/10;		m = m*10+n%10;			}	return sign*m;}
  

二叉树左右孩子交换

• void TreeReverse(Tree * p){	Tree * temp;		if(p){		temp  = p->left;		p->left = p->rigth;		p ->rigth = temp;		TreeReverse(p->left);		TreeReverse(p->rigth);		}	}
  

二叉树找到x的兄弟节点

• Tree * findNode(Tree * p ,int x){ Tree *temp = p; if(p){	if(p->left!=NULL || p->rigth!=NULL){	 if(p->left->x == x){				if(p->rigth){		 p = p->rigth;		 printf("\n find succee  %d",p->x);		 return p;		}					 }	 if(p->rigth->x == x){				if(p->left){		 p = p->left;		 printf("\n find succee  %d",p->x);		 return p;		 		}	 }	 	}	 	temp = findNode(p->left,x);	if(temp){		return temp;			}	temp = findNode(p->rigth,x);		return temp;		  }else {	return NULL;	}}
  

二叉树递归查找

• Tree * finderNode(Tree * p,int data){	Tree * temp = p;		if(p){		if(p->x ==data){			return p;					}		temp = finderNode(p->left,data);		if(temp){			return temp;		}		temp = finderNode(p ->rigth,data);		return temp;			}else {		return NULL;			}	}
  

二叉搜索树查找

• Tree * findSearch(Tree* p ,int data){	while (p) {		if(p->x >data){			p = p->left;		}else if(p -> x <data){			p= p->rigth;					}else {			break ;					}	}	return p;}
  

链表尾插入一个元素算法

二叉搜索树插入节点

• void binaryTreeInsertNode(Tree * head,int data){	Tree * node = newNode(data);	Tree * p =head;	Tree * partent =p;	while (p) {		partent = p;				if(p->x < data){						p = p->rigth;					}else if(p->x >data){			p = p->left;					}else {			return;			//不许插入相同元素节点		}	}	if(head == NULL){		//空树		partent = node;			}else {		if(partent->x < data){			partent->rigth = node;					}else {			partent->left = node;		}	}	}
  

二叉树找出最大值

• int TreeMaxNode(Tree * p ,int data){	int max =data;	if(p){		if(max<p->x){			max = p->x;		}		max = TreeMaxNode(p->left,max);		max = TreeMaxNode(p->rigth,max);		return max;	}else {		return max;			}}
  

二分查找

• int binarySearch(int array[],int left ,int right,int data){	int i = left;	int j = right;	while (i <= j) {		int mid = (i + j)/2;		if(data == array[mid])return mid;		else {			if(data <array[mid]) {				j =mid-1;			}else {				i = mid+1;			}		}	}	return -1;	}
  

链表逆序

• Link* linkReverse(Link * L){	Link * left = NULL ,*mid = L->next ,*right = NULL;	while (right) {		right = mid->next;		mid ->next = left ;		left = mid;		mid = right;	}	right = newNode(0);	right ->next  =mid;	return right;}//有表头节点的逆序Link ListReverse(List & L){	link last = 0 ,cur= L->first , next;	while (cur) {		next = cur ->next ;		cur ->next = last;		last = cur;		cur = next;			}	L->first = last;	}//书中不带表头节点链表
  

两个有序单链表合并

• 懒得写了，判空，确定L3点表头，p1&&p2循环判断连接进L3
• 处理剩余元素，断开L1L2，返回L3

两个递减的有序链表合并为一个递增的有序表，lc指向

• 可以分别递增排序两个递减有序表，然后合并
• 或者以两个递减有序表合并成一个有序表，然后递减有序表直接反转reverse

杨辉三角

• #include "stdio.h"#include "string.h"#include "math.h"#include "stdlib.h"#define N 10int main(){	int i,j;	int s[N][N]={0};//初始化一定要做好	//	初始化，第一列，对角线	for (i=0;i<N;i++){		s[i][0]=1;		s[i][i]=1;	}	//	中间内容，s[1][0]开始,数值为2，s[i][j]=s[i-1][j-1]+s[i-1][j];		for (i=2;i<N;i++) {		for (j=1;j<=i-1;j++) {			s[i][j]=s[i-1][j]+s[i-1][j-1];		}	}	//	输出 for for j=0;j<i  三角形输出	for(i=0;i<N;i++){		for	(j=0;j<=i;j++){			printf("%5d",s[i][j]);		}		putchar(10);	}}    1    1    1    1    2    1    1    3    3    1    1    4    6    4    1    1    5   10   10    5    1    1    6   15   20   15    6    1    1    7   21   35   35   21    7    1    1    8   28   56   70   56   28    8    1    1    9   36   84  126  126   84   36    9    1
  

Fibonacci

• //递归式int fibonacci(int n){	if(n<=1)return 1;	return fibonacci(n-1)+factorial(n-2);	}//动态规划//保存已经计算过子问题的解，避免重复计算int Fibonacci(int n){	int *f =(int *)malloc(sizeof(int)*(n+1));	f[0]=f[1]=1;	for (int i=2;i<=n;i++) {		f[i]=f[i-1]+f[i-2];	}  free(f);	return f[n];  }//动态规划//只使用了两个位置，十分精妙，单数时，存放在1位，双数时存放在0位，反复叠加，最后在单数停下所有的叠加int fibonacci2(int n){	int f[2] ;	f[0]=f[1]=1;	while (--n) {		f[n&1]=f[0]+f[1];	}	return f[1];}
  

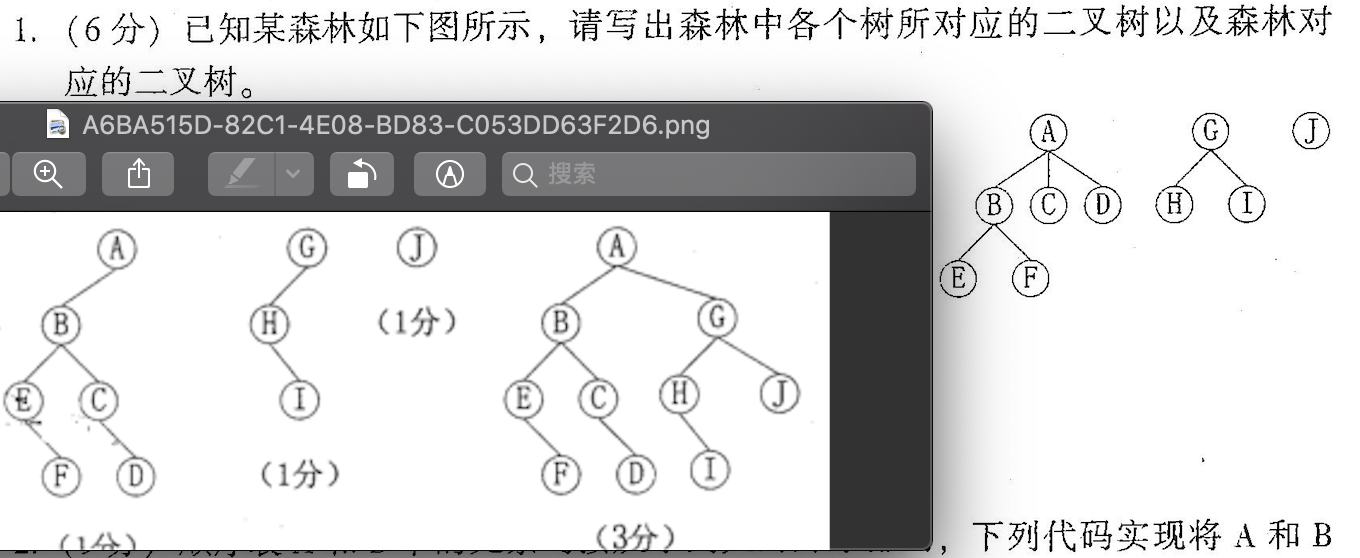
##森林转二叉树

• 

锻炼思维问题

rand & srand

#include "stdio.h"
#include "stdlib.h"
#include "time.h"
int main(){
	int s[10]={0};
	int t;
	
	srand(time(0));//use current time as seed for random generator
	for (int i=0;i<10;i++) {
		s[i]=rand()%100;
		printf("%5d",s[i]);
	}
	putchar(10);
	printf("rand_max:%d\n",RAND_MAX);
	for(int i=0;i<10-1;i++){
		for(int j=i+1;j<10;j++){
			if(s[i]>s[j]){
				t= s[i];
				s[i]=s[j];
				s[j]=t;
				
			}
		}
	}
	for (int i=0;i<10;i++) {
		printf("%5d",s[i]);
	}
  printf("\n%d", 1 + rand()/((RAND_MAX + 1u)/100));
  //1u表示无符号整型，系统默认有符号整型，unsigned
}



   70   54   82   63    6   33   22   56   46   79
rand_max:2147483647
    6   22   33   46   54   56   63   70   79   82
86

字符串问题

int main(){	
	char s[] = "12345678";
	printf("%s\n",&s[1]);//第二个地址开始遍历，遍历到‘\0’结束
	printf("%s\n",&s[0]);//作为第一个地址
	printf("%s",s);//数组名作为数组的第一个地址，不用&取地址符
	
}
2345678
12345678
12345678

#include "string.h"
int main(){	
	char a[10], b[]="adsffadsfsaf"	;
	strcpy(a,b);
}
//copy存放的空间不足直接报错,不截断

//Terminated due to signal: ILLEGAL INSTRUCTION (4)

二维数组越界问题

#include <stdio.h>

int main(int argc, char *argv[]) {
	int a[][2]={1,2,3,5,6};
	
	for (int i=0;i<3;i++) {
		for (int j=0;j<2;j++) {
			if (a[i][j]=='\0') {
				continue;
				
			}
			printf("%d ",a[i][j]);
			
		}
	}
	printf("\n %d ",a[0][4]);
	printf("\n %d ",a[0][5]);
	printf("\n %d ",a[0][6]);
	
}


Untitled 3.c:16:18: warning: array index 4 is past the end of the array (which contains 2 elements) [-Warray-bounds]
        printf("\n %d ",a[0][4]);
                        ^    ~
Untitled 3.c:4:2: note: array 'a' declared here
        int a[][2]={1,2,3,5,6};
        ^
Untitled 3.c:17:18: warning: array index 5 is past the end of the array (which contains 2 elements) [-Warray-bounds]
        printf("\n %d ",a[0][5]);
                        ^    ~
Untitled 3.c:4:2: note: array 'a' declared here
        int a[][2]={1,2,3,5,6};
        ^
2 warnings generated.
1 2 3 5 6 
 6 
 0 
          ns 2 elements) [-Warray-bounds]
        printf("\n %d ",a[0][6]);
                        ^    ~
Untitled 3.c:4:2: note: array 'a' declared here
        int a[][2]={1,2,3,5,6};
        ^
3 warnings generated.
1 2 3 5 6 
 6 
 0 
 -1591672656 
          
        

• 可以看出2个问题
  • 初始化
    • 只设置了列的参数，为2，没设置行，编译器自动计算，分配成了三行
    • 每一行没有’\0’结尾
    • 规定列数后，自动计算行数，没有在花括号中初始化的数组位置被默认以3行2列初始化，所以a[2] [1] = ‘\0’
  • 内存排列
    • 
    • 在内存中，所有的行连续存储在存储器中（随便找的图，意思是这个意思）
    • 所以访问a[0] [5]会输出0 对应的就是a[2] [1] 中的’\0’
    • 最后超出a[0] [6]不在数组初始化范围内，所以数据随机
    • 超出范围编译器进行警告但没有报错

extern&内部&外部变量注意

• 区域划分
  • 全局
  • 局部
• 存储区域划分
  • 动态
    • 自动auto
  • 静态
    • 手动
    • static 或全局
  • 寄存器register
    • 自动了，不能写在函数外
• 局部静态变量
  • 决定
• 全局变量
  • 范围从定义位置开始到本文件执行结束，可以通过extern扩展到同项目中的其他文件
  • 全局静态变量
    • 只限本文件中，从定义位置开始到本文件结束范围，其他文件无法使用extern扩展访问范围

指针强制转换赋值问题

#include <stdio.h>

int main(int argc, char *argv[]) {
	int a=0;
	double *b;
	b=&a;
	int * c;
	c=&a;
	printf("b pointer:%d\n",b);
	printf("a pointer:%d\n",&a);
	printf("c pointer:%d\n",c);
	printf("sizeof a %d\n",sizeof(a));
	printf("sizeof b %d\n",sizeof(b));
	printf("%d\n",*b);
	printf("%d",*c);
	return 0;
	//指向的地址相同，指针的内容不仅包裹纯地址还包括了，还包括了数据的类型，数据的存储方式和使用的内存空间可能不同，
	//b=&a;进行了强制转换，将a为int型的地址转换为double型的地址赋值给b，但是因为基类型是不同的，地址相同得出的数据也是不同的，地址相同也只是指地址的起始位置相同，int占用的是4个字节存储数值，超出范围的内存是未知的，double的大小是8个字节，四个字节中长度未知，所以得出的数值是根据double的运算方法从8个字节的内存中计算得出的；

}

C用函数改变指针指向

#include <stdio.h>
void SwapPointer(int **,int **);
void Swap(int *a,int *b);
void SwapP(int *a,int *b);
	
int main(int argc, char *argv[]) {
	int a=1,b=2;
	int *a1=&a,*b1=&b;
	
	printf("原值 a:%d b:%d\n",a,b);
	printf("原值 a1:%d b1:%d\n",a1,b1);
		
	printf("Swap:\n");
	
	Swap(a1, b1);
	//普通的 传引用  方式交换 a b值
	//a1 的值是 变量a的地址  ，传递给函数的是a1的值，变量a的地址，交换了int 型指针变量a1 的指向，使其指向变量b，
	
	
	printf("	a:%d b:%d\n",a,b);
	printf("	a1:%d b1:%d\n",a1,b1);
	
	
	//错误例子示范
	SwapP(a1, b1);
	//企图通过函数改变指针指向，没有考虑好给函数的实参和SwapP的形参之间的关系是值传递的关系，Swap中的a和b只拿到了实参的值，就是a和b的地址或&a &b,也别想直接交换a和b的地址，变量从创建以来，地址就已经固定，不会改变
	printf("SwapP:\n");
	printf("	a:%d b:%d\n",a,b);
	printf("	a1:%d b1:%d\n",a1,b1);
	
	//============通过函数改变指针指向============
	//根据上面，实参和形参的传递方式是值传递方式，只要改变值传递的方式就通过函数改变指针的指向
	
	SwapPointer(&a1,&b1);
	//传递 指针的地址 给 指针的指针
	printf("SwapPointer:\n");
	printf("	a:%d b:%d\n",a,b);
	printf("	*a1:%d *b1:%d\n",*a1,*b1);
	printf("	a1:%d b1:%d\n",a1,b1);
	
}
void SwapPointer(int **a,int **b){
	int *temp;
	temp = *a;
  //传入的是指针变量的地址，及指针的指针，或指向指针的指针
	//a的值是a1的地址，用temp来临时存放a1的地址
	*a  =*b;
	*b = temp;
	
}
void Swap(int *a,int *b){
	int temp;
	temp = *a;
	*a = *b;
	*b = temp;
	
	
}
void SwapP(int *a,int *b){
	int *temp;
	temp = a;
	a = b;
	b = a;
	
}

指针与数组的注意事项

#include <stdio.h>int main(int argc, char *argv[]) {	int a[10]={1,2,3,4,5,6,7,8,9,10};	int *p;		for (p=a;p<a+10;p++) {		printf("%d ",*p);	}	putchar(10);	p=a;		for (int i=0;i<10;i++) {		printf("%d ",*(p+i));	}	//第一种的速度是比第二种的速度要快，使用   []   变址运算符，会转换为*（a+i）的形式，经过一次计算得出元素地址，速度会比第一种慢	}

二维数组指针 基类型问题

#include <stdio.h>


int main(int argc, char *argv[]) {
	int a[2][8]={11,20,3,4,5,6,7,8,9,10};
	int *p;
	int *b = *(a+0)+0;

	p=a;
	for (int i=0;i<2;i++) {
		for (int j = 0;j<8;j++) {
			if (j%8==0) {
				printf("\n");
			}
			printf("(%d,%d)  ",&a[i][j],a[i][j]);
	
		}
	}
	putchar(10);
	
	printf("%d p\n",p);
	printf("%d a\n",a);
	printf("%d *a\n",*a);
	printf("%d a+1\n",a+1);
	printf("%d *a+1\n",*a+1);
	printf("%d *(a+1)+1\n",*(a+1)+1);
	printf("%d *a+1\n",*a+1);//可以转为*(a+0)+1
	printf("%d **a+1\n",**a+1);//&a[0]上的值+1，就是a[0][0]+1
	
	printf("%d  *a+1+1\n",*a+1+1);//先进行指针运算
	
	printf("%d  (*(a+0)+1)\n",(*(a+0)+1));
	printf("%d  *(*a)\n",*(*a));
	printf("%d  *a\n",*a);
	printf("%d  &*(a+0)\n",&*(a+0));
	
	
	printf("%d sizeof(a[1][1])\n",sizeof(a[1][1]));
	printf("%d sizeof(a[0])\n",sizeof(a[0]));
	printf("%d sizeof(*a)\n",sizeof(*a+1));
	printf("%d sizeof(*a)\n",sizeof(a));
	//二维数组指针  基类型 问题

	printf("%d sizeof(a)\n",sizeof(a));//指针a的基类型是  int型的二维数组
	printf("%d sizeof(*a)\n",sizeof(*a));//指向的是二维数组的第一列，指向一维数组，可通成*（a+0）或a[0]
	printf("%lu sizeof(*a)\n",sizeof(*(*(a+0)+0)));//指向的是二维数组的第一列，指向一维数组，可通成*（a+0）或a[0]
	printf("%d (*(a+0)+0)\n",*(a+0)+0);
	printf("%d (*(a+0)+0)\n",sizeof(*(a+0)+0));//指针变量大小为8
	int *d;
	printf("%d *d\n",sizeof(d));//指针变量大小为8，什么类型都为8
	double *e;
	printf("%d *e\n",sizeof(e));
	
}
	
//	(-339044768,11)  (-339044764,20)  (-339044760,3)  (-339044756,4)  (-339044752,5)  (-339044748,6)  (-339044744,7)  (-339044740,8)  
//	(-339044736,9)  (-339044732,10)  (-339044728,0)  (-339044724,0)  (-339044720,0)  (-339044716,0)  (-339044712,0)  (-339044708,0)  
//	-339044768 p
//	-339044768 a
//	-339044768 *a
//	-339044736 a+1
//	-339044764 *a+1
//	-339044732 *(a+1)+1
//	-339044764 *a+1
//	12 **a+1
//	-339044760  *a+1+1
//	-339044764  (*(a+0)+1)
//	11  *(*a)
//	-339044768  *a
//	-339044768  &*(a+0)
//	4 sizeof(a[1][1])
//	32 sizeof(a[0])
//	8 sizeof(*a)
//	64 sizeof(*a)
//	64 sizeof(a)
//	32 sizeof(*a)
//	4 sizeof(*a)
//	-339044768 (*(a+0)+0)
//	8 (*(a+0)+0)
//	8 *d
//	8 *e	

指向指针的指针

#include <stdio.h>#include "string.h"void SortString(char *string[],int N);void PrintString(char *string[],int N);int main(int argc, char *argv[]) {	char *string[4]={"B","A","C","D"};//	SortString(string, 4);//	PrintString(string, 4);			char **p=string;	printf("string :%d\n",string);	printf("*string :%s\n",*string);	//string 的值就是“B”字符串常量的地址	printf("p: %d\n",p);	//输出的是p的值，p的值存放的是string中存放的值，及“B”字符串常量的地址	printf("*p: %s\n",*p);	//p和string是同级关系，存储的值相同，但是是两个不同的指针，指向同一个地址		}void SortString(char *string[],int N){	int k;		for (int i=0;i<N-1;i++) {		k=i;				for (int j=i+1;j<N;j++) {			if (strcmp(string[k], string[j]) > 0) {				k=j;							}		}		if(k!=i){			char * temp=string[k];			string[k]=string[i];			string[i]=temp;			//改变指针指向					}	}}void PrintString(char *string[],int N){	for (int i=0;i<N;i++) {		printf("%s\n",string[i]);		//直接按原顺序输出就行			}}string :-523356560*string :Bp: -523356560*p: B

有趣的指针题

#include <stdio.h>#define N 10void min_max_swap(int *array);int main(int argc, char *argv[]) {	int array[N]={97,1,2,3,4,5,6,7,8,9};	printf("%d      \n",*(array+N-1));		int *p=array;	printf("%d\n",p);	printf("%d\n",*p++);	//使用++前的值	printf("%d\n",p);		int *p2 = array;	printf("%d\n",p2);	printf("%d\n",*++p2);	//使用++后的值	printf("%d\n",p2);		min_max_swap(array);				for (int *p = array;p<array+N;p++) {		printf("%4d,",*p);			}	printf("\b");	}void min_max_swap(int *array){	int *min,*max,temp;	min=max=array;	for (int *p=array+1;p<array+N;p++) {		if(*p > *max){			max = p;		}else if(*p < *min){			min = p;					}	}	temp = *array;	*array = *min;	*min = temp;		if (max == array) {		max = min;			}	temp = *(array+N-1);	//注意最后一个位置是9，不是10，容易越界	//注意优先级问题	//*优先级高于+	//但++的优先级又高于*		*(array+N-1)=*max;	*max = temp;			//先都指向首地址	}

结构体易错点记录

#include <stdio.h>int main(int argc, char *argv[]) {	struct Lwh{		int i;		char j;		float a;		double b;		}lwh1 ={.i =10,.b = 2};//这种方式对单独成员初始化		struct Lwh lwh2 = {.b=3},lwh3; //这种写法，不能先定义再初始化//	lwh3 = {.j='a'};//不能分开写	printf("%d\n",lwh3.j);	printf("%d\n",lwh1.i);	printf("%d\n",lwh1.j);	printf("%f\n",lwh1.a);	printf("%f\n",lwh1.b);	printf("%f lwh2 \n",lwh2.b);//	10//	0//	73896//	2.000000//	3.000000 lwh2 	//char型默认初始化为'\0',指针初始化为NULL，数值型初始化为0}

结构体内存占用情况

#include <stdio.h>int main(int argc, char *argv[]) {	struct Lwh{		int i;		char j;		float a;		double b;					}lwh1 ={10,'a',12,13};//这种方式对单独成员初始化	printf("%lu &lwh1\n",&lwh1);	printf("%lu i\n",&lwh1.i);	printf("%lu j\n",&lwh1.j);	printf("%lu a\n",&lwh1.a);	printf("%lu b\n",&lwh1.b);	printf("%lu &lwh+1\n",&lwh1+1);//+1的基类型是以结构体为单位，这样的方法应该结合结构体数组，和结构体指针，位置停留在结构体的末尾	//根据内存显示，结构体占用情况分别是4、4、8、8，此结构体占用总空间为24	printf("%lu \n",sizeof(lwh1));	printf("%lu \n",sizeof(double));	printf("%lu \n",sizeof(float));	//占用的空间并不和原类型大小完全一致	}

#include <stdio.h>int main(int argc, char *argv[]) {	struct Lwh{		int i;		char j;		float a;		double b;					}lwh1 [3]={{11,'a',21,31},{12,'b',22,32},{13,'c',23,33}};	struct Lwh *lwhp = lwh1;		printf("%d (*lwhp).i\n",(*lwhp).i);	printf("%d lwhp->i\n",lwhp->i);	printf("%d (*(lwhp+1)).i\n",(*(lwhp+1)).i);	//理清关系	//（lwhp+1）在内存层面上，根据结构体分配的内存大小，加上一个结构体的内存大小，将位置从第一个结构体到头部移动到第一个结构体到尾部，正是第二个结构体头部	//(*(lwhp+1))成员运算符‘.’比 *取值符 优先级高，当前层面是内存层面，需要进行一次取值操作，取出结构体值，	//最后才是找到结构体中成员的部分.i	printf("%d (lwhp+1)->i\n",(lwhp+1)->i);	//内存层面+1，然后直接指向成员i			}

enum初始化问题

#include <stdio.h>enum test{a=5,c,d,e,f=1,g=1,h,i,j,k}A；//单独指定值后，后面未指定的值+1，不指定值默认从零开始加，相同的值也是有的  int main(int argc, char *argv[]) {	A =a ;	printf("%d\n",A);	printf("%d\n",c);	printf("%d\n",d);	printf("%d\n",e);	printf("%d\n",f);	printf("%d g\n",g);	printf("%d\n",h);	printf("%d\n",i);	printf("%d\n",j);	printf("%d\n",k);		}567811 g2345

不使库函数（abs）通过位运算实现取一个整数的绝对值

问题出自：2017年韩山师范学院本科插班生考试 第3题

• 

需要用到的知识点

• 原码、补码、反码
• 负数转2进制
• 位运算
• 2进制乘法（关系不大）

解题代码：

• int myabs(int n){	return n * ((n>>31<<1) +1);}
  

• 整型变量 n 右移31位 左移1位 +1 乘 n

原码

• 正数的原码就是它本身，符号位 为 0
• 负数符号位为1，八位二进制举例：1000 1010 = （-10）10

反码

• 正数的反码和原码相同
• 负数的反码符号位置不变，其他按位取反，整数-10的反码是：1111 0101

补码

• 正数的补码和原码一样
• 负数的补码为反码+1 整数-10的补码是：1111 0110 这就是整数-10在计算机中的存储形式

负数转二进制

• 计算机中没有直接做减法，是通过加法来实现的，所以负数在计算机中是由原码的补码+1得到的
• 符号位为1，符号为不变
  • 原码转补码：取反+1
  • 补码转源码：-1取反

位移运算

左移运算<<

• 低位补零，高位溢出
• 不溢出的情况下相当于乘2

右移运算>>

• 逻辑右移&&算数右移
  • 对无符号数，右移时高位补零，低位溢出
  • 对于有符号数，原来是0，同上，原来是1（即负数），左边移入0还是1，取决于计算机系统，有系统补0有系统补1，补 0 的称为逻辑右移，补 1 的称为算数右移
  • 举例
    • 1011 0011
    • 0101 1001（逻辑右移）
    • 1101 1001（算数右移）
  • Visual C++和其他C编译器采用算数右移，有符号数右移时，原符号位为1，左边高位补1

二进制乘法

• 举例：

• 

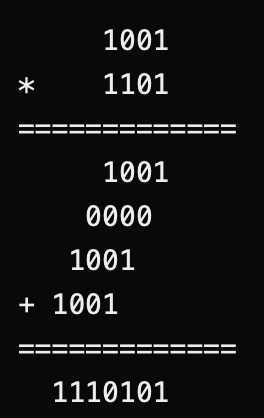
解题

• //以-2为 n 举例
  //n * ((n>>31<<1)+1)
  //-2*(-2>>31<<1)+1  
  
  
  1000000000 0000000000 0000000000 10
  //-2的原码
    
  1111111111 1111111111 1111111111 01
  //-2的反码
    
  1111111111 1111111111 1111111111 10
  //-2的补码  -2反码+1
  //这是-2 在计算机中的表示  以源码的补码表示
  
  
  1111111111 1111111111 1111111111 11
  //-2 >> 31
  1111111111 1111111111 1111111111 10
  //<< 1
  1111111111 1111111111 1111111111 11
  //+1
  //这是-1在计算机中的表现形式
    
  //补码转源码：符号位不变，减1取反
  1000000000 0000000000 0000000000 01
  //-1  原码
    
  //-2 * -1 = 2   最后得出n的绝对值为2
    
  //正数就不举例了
  
  

博客参考

• https://blog.csdn.net/zhang429350061/article/details/41803469

字符串的几种初始化方式

• #include <stdio.h>
  #include "stdlib.h"
  #include "string.h"
  int main(int argc, char *argv[]) {
  	char a[]={"abc"};
  	char b[]="abc";
  	char c[]={'a','b','c','\0'};
  	char d[]={'a','b','c','\0'};
  	char *e = (char *)malloc(sizeof(char)*4);
  	//其他属于局部变量，退出所在函数会被释放，这种方式需要手动释放free
  	strcpy(e,"abc");
  	
  	char g[]={'a','b','c'}; 
  //	printf("%s",g);abc‡X¿õ⁄没有找到结尾乱码
  	
  	printf("%d",strlen(c));
  	printf("%d",strlen(g));//长度为9
  	//不计算\0;
  
  	//被认为是一个3字节的字符数组，所以没有预留\0的空间，对很多字符串的操作将出错
  	
  //	char *f ="abc";  这种定义的字符串是常量
  		
  }
  

动态二维数组

#include <stdio.h>#include "stdlib.h"#include "string.h"int ** malloc2d(int r,int c);int main(int argc, char *argv[]) {		int ** t;	t = malloc2d(2, 3);		//多种赋值方式	*(*(t+0)+1)=1;	*(*(t+1)+2)=2;	t[1][1]=3;		for (int i=0;i<2;i++) {		//单循环或双循环		for (int j = 0 ;j<3;j++) {			printf("%d  ",*(*(t+i)+j));		}		putchar(10);			}  free(t);			}//row 行//column 列//主要是这两条申请语句int ** malloc2d(int r,int c){	int ** t= (int ** )malloc(r*sizeof(int*));	for (int i=0;i<r;i++) {		t[i] = (int *)malloc(c*sizeof(int));		//初始化，不初始化默认的数值也默认0		for (int j=0;j<c;j++) {			*(*(t+i)+j) = 0;								}			}	//从零列开始	return t;	}0  1  0  0  3  2  

实战思考题

N! N的阶乘

#include <stdio.h>

int main(int argc, char *argv[]) {
	int fac (int a);
	printf("%d ",fac(10));
	
}
int fac (int a){
	int f;
	
	if(a<0){
		printf("阶乘不能小于0");
	}else if(a==0||a==1){
		f=1;
		
	}else{
		f=fac(a-1)*a;
	}
	return f;
}


3628800 

递归移动盘子

#include "stdio.h"
void hanoi(int n,char one,char two,char three);
int main(){
	hanoi(3, 'A', 'B', 'C');
	
}
void hanoi(int n,char one, char two,char three){
	//从one移动到three需要借助two
	void move (char x, char y);
	if (n==1) {
		move(one, three);
		//当n=1时，代表只剩一个盘子需要移动，最后一个盘子从one移动到three不需要借助其他位置
	}else {
		hanoi(n-1, one, three, two);
		//第一个操作，从第一个位置移动到第二个位置，借助three位置
		move(one,three);
		hanoi(n-1, two, one,three);
	}
}
void move (char x,char y){
	printf("%c -> %c \n",x,y);
}

//解体思路：
//一个盘子直接从A-C
//两个盘子要：A-B、A-C，B-C
//只要看懂两个盘子如何移动，结合一个盘子移动，就能写出顺序

杨辉三角

#include "stdio.h"
#include "string.h"
#include "math.h"
#include "stdlib.h"
#define N 10
int main(){

	int i,j;
	int s[N][N]={0};//初始化一定要做好
	
//	初始化，第一列，对角线
	for (i=0;i<N;i++){
		s[i][0]=1;
		s[i][i]=1;
	}
	
//	中间内容，s[1][0]开始,数值为2，s[i][j]=s[i-1][j-1]+s[i-1][j];
	
	for (i=2;i<N;i++) {
		for (j=1;j<=i-1;j++) {

			s[i][j]=s[i-1][j]+s[i-1][j-1];
		}
	}
	
//	输出 for for j=0;j<i  三角形输出
	for(i=0;i<N;i++){
		for	(j=0;j<=i;j++){
			printf("%5d",s[i][j]);
		}
		putchar(10);
	}
}

    1
    1    1
    1    2    1
    1    3    3    1
    1    4    6    4    1
    1    5   10   10    5    1
    1    6   15   20   15    6    1
    1    7   21   35   35   21    7    1
    1    8   28   56   70   56   28    8    1
    1    9   36   84  126  126   84   36    9    1

十六进制转十进制

#include <stdio.h>
int htoi(char s[]);
int main(int argc, char *argv[]) {
	char array[1]="a";
	printf("%c  ",array[0]);
	printf("%d",htoi(array));

}
int htoi(char s[]){
	int i,n;
	n=0;
	for (i=0;s[i]!='\0';i++) {
		if (s[i]>='0'&&s[i]<='9') {
			n=n*16+s[i]-'0';
		}
		if (s[i]>='a'&&s[i]<='f') {
			n=n*16+s[i]-'a'+10;
		}
		if (s[i]>='A'&&s[i]<='F') {
			n=n*16+s[i]-'A'+10;
		}
	}
	return n;
//	a11
//	((0*16+'a'-'a'+10)*16+'1'-'0')*16+'1'-'0'
//	10*16+1*16+1
//	160*16+1
//	=(10*16^2)+(1*16^1)+(1*16^0)
//	=2560+16+1
//	=2577
//	
	
}

递归字符转换

  #include <stdio.h>
  void convert(int );
  int main(int argc, char *argv[]) {
    convert(10);
  }
  void convert(int n){
    int i;

    if((i=n/10)!=0){
      convert(i);
    }
    putchar(n%10+'0');//字符转换+‘0’
    putchar(32);
  }

字符串复制函数改进过程

void copy_string(char * from,char * to){
  
  //方法1
	while ((*to=*from)!=0) {
		to++;
		from++;
		//省去了最后*to=‘\0‘的操作
	}
	//方法2
	{
		while ((*to++=*from++)!=0);
		//先++，然后*，赋值，判断，循环
	}
	//方法3
	//判断是否等于0可以直接作为循环判断条件，
	{
		while (*from) {
			*to++=*from++;
			
		}
		*to='\0';
	}
	//方法4
	//再简化
	{
		while (*to++=*from++);
    //这句是真的好用，自己找到结尾
	}
	
	
}

简洁计算字符串长度

#include <stdio.h>int main(int argc, char *argv[]) {	char  str[20];	scanf("%s",str);	//字符指针指向没设定长度的字符串常量，不能进行修改，scanf不能输入	char * p = str;	int i=0;	while (i++,*p++);	//逗号运算符	printf("%d",i-1);	//while结束时，结果会多一次，注意	}

LinkedList 动态链表实现

#include <stdio.h>#include <stdlib.h>#define SIZE sizeof(struct Link)struct Link{	int num;	float score;	struct Link * next ;	};struct Link * create(void);int main(int argc, char *argv[]) {	struct Link *pt;	pt = create();	while (pt->next) {		printf("%d %f print\n",pt->num,pt->score);		pt = pt->next;		//输出完指向下一个节点，直到==null	}	return 0;	}//返回头节点struct Link * create(void){	struct Link * head,*P1,*P2;	int n=0;		P1=P2=malloc(SIZE);//返回的是一个地址	head = NULL;	scanf("%d,%f",&P1->num,&P1->score);	while (P1->num) {		n++;		//第一次head指向链表头		if(n==1){			head = P2;		}		P1 = malloc(SIZE);		//申请内存空间，赋值给P1空间		P2->next = P1;		//通过成员next存放下一个节点的地址，将两块内存进行连接		P2= P1;		//”重新定位“，此时P1的next还是null，进行下一个节点的连接就要像这个新节点定位，用这个新节点的next存放下一个新节点		//因为这是单向链表，所以上一个节点的位置已经不需要知道了，所以让P2指向P1，待下一个新节点申请再链接		scanf("%d,%f",&P1->num,&P1->score);		//P1赋值				}	P1->next = NULL;	return head;	}	

常用链表操作

• 
• 
• 
• 插入
• 
• 
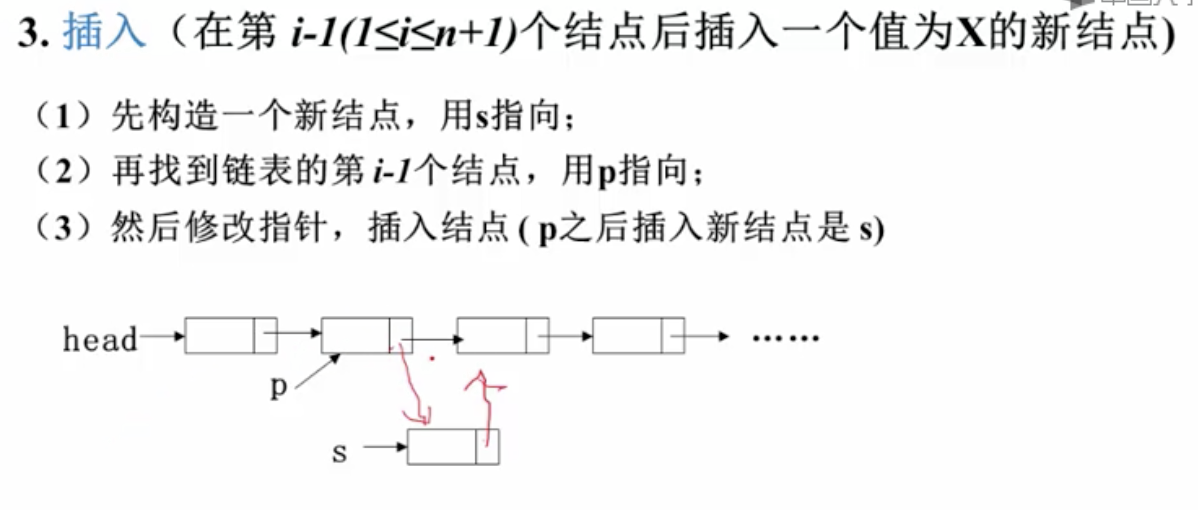
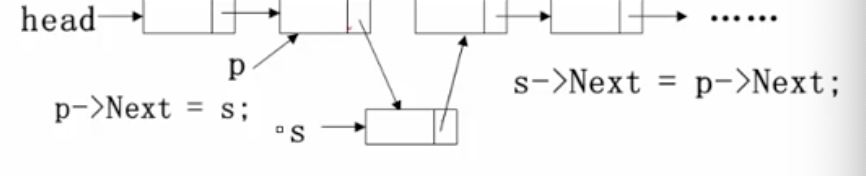
• 顺序不能调转
• 
• 
• 

C语言题目收集

• 3．能表示“整型变量x的绝对值小于5”的C语言表达式是________x*((x>>31<<1)+1) < 5______ (不得使用系统函数)。
• 7．在C程序中，根据数据的组织形式可以可分为_____二进制文件______文件和______文本文件_____文件。
• 8．若有定义chars[]=“\n123\”;则strlen(s)的值为___5____；sizeof(s)的值为___6___。
• char *a = “\007”; 直接结尾为空 赋值时直接指向 \0 ,整个字符串空，但是可以定义不违法
• char c = '\ '; 编译报错，注意使用转义字符 \ 将单引号注释 直接不合法
• double d = 1.5E2.0; 科学计数法，指数位不能为小数，可以为负数 不合法
• int a = 1,200 不能加逗号 不合法
• if((j++ || k++) &&i++) printf(“%d,%d,%d\n”,i,j,k); 进行的短路运算，j++完成后就不进行k++运算
• 定义数组不能包含变量，属于动态定义，可以包含常量和符号常int a[3+5]合法，
• printf(“%d”,a+=a-=a=9); 优先同级从右往左，结果为0

演示函数

阶乘

int factorial (int n){	if(n==0)return 1;	return n*factorial(n-1);}

Fibonacci数列

//递归式
int fibonacci(int n){
	if(n<=1)return 1;
	return fibonacci(n-1)+factorial(n-2);
	
}

//动态规划
//保存已经计算过子问题的解，避免重复计算
int Fibonacci(int n){
	int *f =(int *)malloc(sizeof(int)*(n+1));
	f[0]=f[1]=1;
	for (int i=2;i<=n;i++) {
		f[i]=f[i-1]+f[i-2];
	}
  free(f);
	return f[n];
  
}

//动态规划
//只使用了两个位置，十分精妙，单数时，存放在1位，双数时存放在0位，反复叠加，最后在单数停下所有的叠加
int fibonacci2(int n){
	int f[2] ;
	f[0]=f[1]=1;
	while (--n) {
		f[n&1]=f[0]+f[1];
	}
	return f[1];
}

	printf("%d\n",3&1);
	//0011
	//0001
	//1
	//f[1] = f[0]+f[1]
	//f[1] = 2
	printf("%d\n",2&1);
	//0010
	//0
	//f[0] = f[0]+f[1]
	//f[0] = 3
	printf("%d\n",1&1);
	//0001
	//1
	//f[1] = f[0]+f[1]
	//f[1] = 5
	

哥德巴赫猜想

• 任何大偶数都可以表示位两个素数相加

/***********判断是不是素数************/int prime(int n){	int i;for(i=2;i<=sqrt(n);i++)//这里就涉及到使用根号的素数判断{	if(n%i==0)	{		return 0;//不是素数返回0	}}	return 1;//是素数返回1	}void print(int n){	int i;	for(i=2;i<=n/2;i++)	{		if(prime(i)&&prime(n-i))//判断拆分出的两个数是不也是素数		{			printf("%d=%d+%d\n",n,i,n-i);			}		}		}

连续整数和问题

• 计算可以表示多少个两个以上连续整数只和
• 9=4+5 = 2+3+4 两个连续整数和

int find(int n){	int b,e,sum,cnt;		b = e = sum = 1;	cnt =0;	while (b<=n/2) {		if(sum<n){			e++;			sum+=e;					}else if(sum >n){			sum-=b;			b++;					}else if(sum == n){			sum -=b;			b++;			cnt ++;					}	}	return cnt;	}

单链表Reverse

• 指针数组调转，转换
• 核心思想，原头做尾，中间每个节点指向原前驱节点，原尾做头
• 参见 习题 21p

双链表Reverse

• 循环双链表，核心思想，交换每个节点的左右指针呢，以head为哨兵循环的结束，交换左右指针后，current = current->left，其实是让current向右走
• 普通双链表，从a(1)开始，current = null 结束
• 笔记参见， 习题 33p

最小公约数 递归

• int gcd (int a,int b){	if(b==0)return a;	return gcd(b,a%b);}//三个数求最小公约数就再加一层
  

数据结构视频笔记

第一章 引论

• 算法

  • 解决问题的一种方法或过程，指令的有限序列，
  • 输入、输出、确定性：指令无歧意，有限性

• 程序

  • 算法用程序语言实现，程序可以不满足算法的有限性，如操作系统可无限循环
  • 操作系统不是算法，而是程序
  • 操作系统的子程序由算法完成

• 理解问题

  • 输入输出
  • 确定数据结构，算法策略
  • 正确性
  • 分析算法，复杂性分析，时间空间复杂性
  • 设计程序

• 算法复杂性

  • 所设计的算法产生的程序，所耗费的资源，保证正确性

  • 计算机资源：时间，空间

  • n是问题的规模

  • 

  • I为n，n为规模，在n规模时，算法使用的时间最大，为最坏

  • 渐进概念

    • 
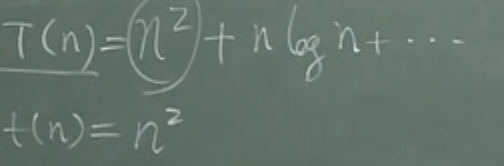
    • 函数T由多种复杂度组合而成，当n趋近与+∞时，复杂度是由什么速度进行增长的
      • 小t(n)为n方，当T（n）减去t（n）剩下低阶项，和T（n）比是无穷小的，所以小t（n）就是大T（n）的渐进形式 ，T（n）排除去低阶项的主项就是它的渐进形态

  • 认识符号概念

    • 

    • n是问题规模，f（n）和g（n）都是复杂性的函数

    • O

      • {} 表示集合
      • ｜ 集合需要具有的属性
      • 举例： O（n^2）函数的集合，在所有的函数之间，当n足够大，都小于等于一个常数乘上n平方 ，以n^{2为上界，的所有的函数都称为O（n}2），不是一个函数的概念，是一个函数集合的概念

    • 欧米伽 下界，计算时间下界由欧米伽

    • 

    • 塞塔 既是上界也是下界

    • f（n）=O（n^{2）这样的表达并不严谨O（n}2）是函数集合的复杂性，应该写成f（n）属于 O（n^2），上面那种也能说，只是一种约定俗成，讲的是f（n）的阶， 是渐进的阶

    • 

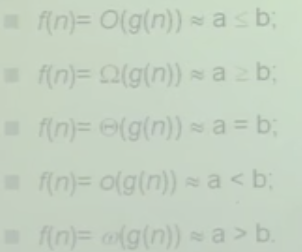
    • 帮助理解函数渐进阶

    • 传递性

    • 

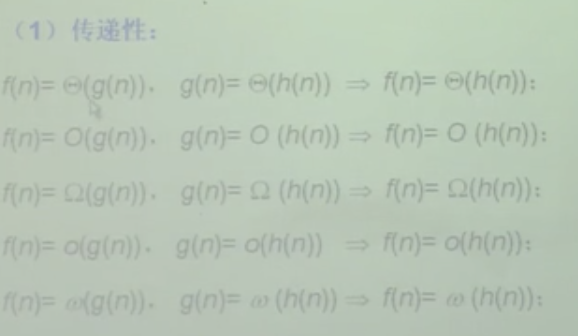
    • 算数运算

    • 

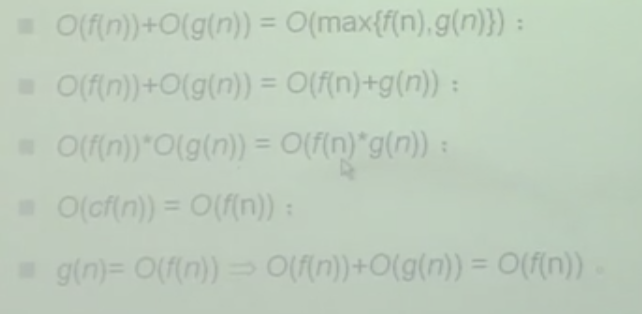
    • O（max{f(n),g(n)})

    • f（n）和g（n）两条曲线，的每个数值点相加就是他的算数运算，这是一个他的渐进性，O的渐进形态，在fn和gn中取一个大的，不是两个函数相加，而是max取一个大的，渐进形态就是取一个大的，如果函数比较复杂，是有拐点的，一段是第一个函数一段是另一个函数

    • [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-YjpGuQe6-1629271689812)(…/…/…/Library/Application Support/typora-user-images/image-20210222021049425.png)]

  • 算法中常用的函数

  • 

  • 单调函数

    • 单调递增，随着n的增加，函数是递增的，就是单调递增
    • 单调递减，随着n的递减，函数递减
    • 严格，函数是否可以相等，严格的不等就是严格单调递增
      • 相等是两条水平线，普通的相等是在一个区间，相等，而严格相等是在任意区间都相等

  • 取整函数不大于x的最大函数，天花板函数

  • 复杂性排序

  • 

数据结构概念

• 反应数据内部的构成，数据由哪些成分构成
• 逻辑上反应了逻辑关系
• 物理上反应了计算机内存储的安排
• 是数据存在的形式

数据类型概念

• 在数据结构的基础上，具有相同数据结构的数据属于同一种类型
• 抽象数据类型
  • 数据类型的延伸，数据模型的以及在数据模型上定义的运算的紧密联系
  • 表也是一种抽象数据类型，对象是给定的元素序列，在给定的元素序列进行的运算，联系在一起称为抽象数据类型
  • 好处
    • 可以使顶层设计和底层实现分离，不考虑数据和数据类型，不考虑在什么场合使用
  • C++实现，用类来实现抽象数据类型
    • 类由四部分组成
      • 类名 同抽象数据类型名对应
      • 数据成员 数据结构对应
      • 成员函数 和运算对应，支持哪些运算
      • 访问级别 公有私有保护

第二章 表

• ADT abstract data type
• 前驱 ，后继
• 逻辑、物理结构
• 逻辑有n个元素
  • 逻辑上相邻的的结构在计算机物理存储中如何实现
• 运算决定他能做什么
• 复杂运算能通过基本的运算组合实现
• 两种存储
  • 顺序存储
  • 链式存储

数组实现表

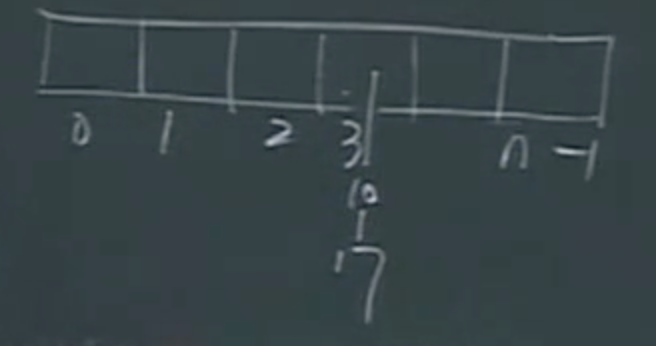
• 约定n=0为空表
• a1为第一个位置
• 插入
  • 最好情况，插入最后一个位置
  • 移动n-k个元素，O（n）
  • 平均要移动n/2
• 删除
  • 删除a(k) 让a(k-1)和a(k+1)相邻
  • 最好情况同上
  • 平均情况，n-1/2
• 优点：不仅要存数据也要存关系，下标存储关系，无需额外的运算存储关系，逻辑相邻物理上也相邻
• 缺点：插入删除需要移动大量元素，容量限制

指针实现表

• 数据结构
  • 数据域
  • 指针域
• 修补空间扩充插入删除的移动
• 时间空间，要么牺牲时间，要么牺牲空间
• 物理上可以不需要相连，但是逻辑上相连
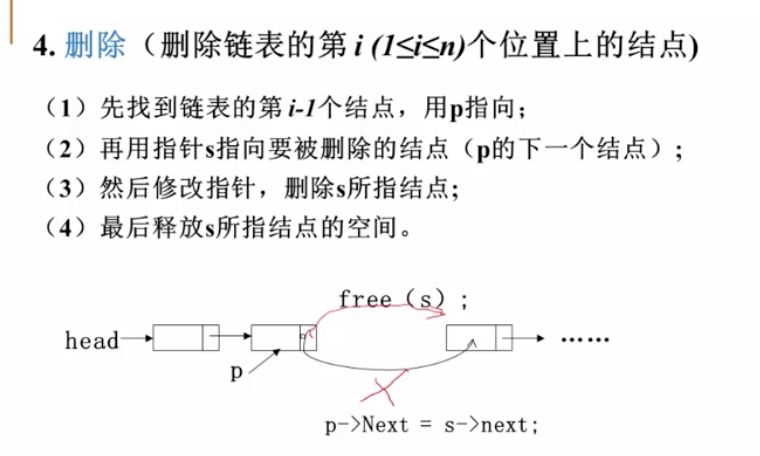
• 在k节点插入和在k节点之后要谨慎考虑，定位在k节点之后插入，不是插入在k+1节点，而是k+1和k之间，定位在k节点之后插入应该定位在k位
  • 如果在k节点插入应该在k-1节点处停下，定位在待插入节点的前一个
• 有些数据结构可能会设置表头节点，不存储元素，书中的是没有表头节点，是first直接指向节点，作为的头节点
  • 设置表头节点的概念就可以忽略新节点插入在表头的情况，因为始终有一个节点不存放元素只是作为first的节点排在第一位，插入头部的方法和插入中间和尾部的方法是一样的
• 插入
  • 其他操作都是默认从k为1开始，但是在插入中，插入的节点是在k值之后的节点，所以在插入中，k是可以为0开始
  • i = 1；i<k 定位在k处，找到k位置，复杂度为O（k），最坏情况是O（n）
  • k为0时是插入在头节点
• 删除
  • 删除位置k，应该定位在k-1节点
    • 如果直接定义在k位，要删除k节点，可以采用将k+1元素存放在k节点，链接k和k+2，删除k+1也能实现删除操作
      • p作为工作指针，在其中定位了k+1的位置，p->next就是k+2的位置
      • p = k->next ; k->element = p->element ; k->next = p->next ; free §
  • k位置是否在范围，链表不为空
  • 是否删除表头节点
  • 如果有表头节点，同上
    • 如果引入表头节点，在插入和删除运算得到统一，一致性的处理，不需要单独考虑头节点位置
  • p= q->next ;q->next = p->next ; free§;
  • 时常要审核程序的健壮性，k是否越界，和q的位置，q表示k-1位置
    • 如链表长度为10，q位置为9，删除10，q要连接的是11位置，没有11位置，就会越界
    • 所以，应该判断 !q || !q->next->next 不为空

间接寻址实现表

• 数组中存放元素的地址，插入时，还需要往后移动，但是移动的是数组中存放的地址，换取较高的效率，地址根据机器的字长，大小是固定的，但是元素可能很大，要移动地址和移动元素消耗的时间可能很大

游标实现表

• 自主调配内存资源，实现是通过存储下标来代替指针的，可以有两个或一个的指针来确定可用数组单元的下标位置，便于分配空间，如果过是一个游标，进行插入和删除会产生内存碎片，游标设定在最后一个位置，只能从后面分配，前面被删除的节点只能变成内存碎片，使用两个游标，有一个就可以指向被删除的位置，要分配内存时先分配那些删除后空出的位置

循环链表

• 书中的循环链表是加入了 表头节点的概念 first节点是不需要存放元素的，使插入和删除得到统一的处理
  • 循环链表中任何一个元素都也作为链表的入口，选择表位作为链表的入口，找到表头和表位的复杂度都为O（1），表头就是last->next,表头不存储元素，last->next->next 就为a（1）的位置
• ListLocate 找x，
  • 确定范围问题，一般两种方法，一种计数器，但是简单的数据结构插入和删除并没有记录数组总长的功能
    • 第二种方法，利用表头节点，将x存放在last->next->element，就是头节点，从第一个节点开始遍历last->next->next，比对element，工作节点p向后推进，判断p->element是否与x相同，跳出循环后判断是中途找到了x元素的位置还是走了一圈碰到p==L->last->next，相同说明走完一圈

双链表

• 需要更快的速度就需要用更多的空间来换取时间，在O（1）时间既能访问到前一个元素，又能访问下一个元素，再将头部和尾部连接起来就实现了，双向循环链表
• 在单链表时，插入时应该定位在k位置，删除时应该定位在k-1位置，虽然定位在k位置也可以，使用双循环链表，就可以在任何节点都可以在O（1）时间找到前驱和后置节点
• 
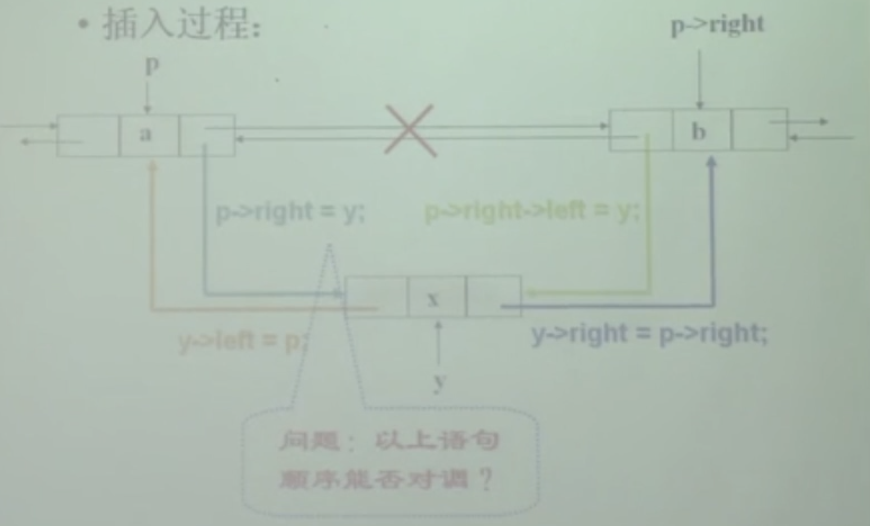
• 进行了y节点的插入，p和p->next的right和left是可以有几种组合的方式赋值的，不局限于这一种，容易因为赋值顺序的交替，导致p->rigth->left定位和想法有出入，可以采用y->right来定位出b的位置 y->right->left = y;
• 双链表还是比较好理解的
• 优点，简化运算，O1时间找到任意元素的前驱节点，简化一些基本运算
• 缺点，消耗空间

第三章 栈 Stark

• 只能在栈顶（表首）进行插入和删除
• 先进后出（FILO），后进先出（LIFO）
• 基本运算，判空满，top返回栈顶元素，push入栈、pop出栈
• 应用，括号匹配问题
  • 字符串反转，回文测试可以用指针指向两段向中间比对
• top初始为-1，用数组实现，元素存放位置t(0…n-1),top应该指向-1
  • 入栈操作应该先移动，再放元素
  • 应选 s[++top] = x
  • 出栈先返回元素再下降
  • top = -1 栈空， top =maxtop -1 栈满
    • 上溢 （underflow） 下溢（overflow）
• 数组实现优缺点，7个基本运算都是O(1)，缺点，需要预设空间
  • 弥补缺点
    • 用两个栈使用同一个数组空间
      • 栈底的分布在数组两端，两个栈的大小动态变化，空间利用率更高
      • 
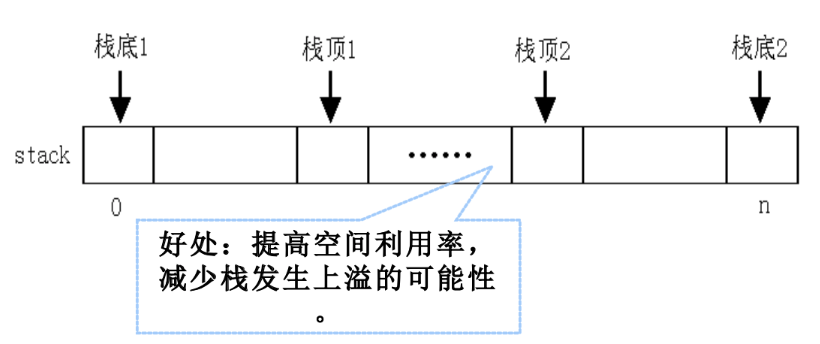
      • 栈满判断，s1->top+1 == s2->top
• 指针实现栈
  • 表头作为栈顶，都是在头节点插入和删除
• 栈实际应用
  • 
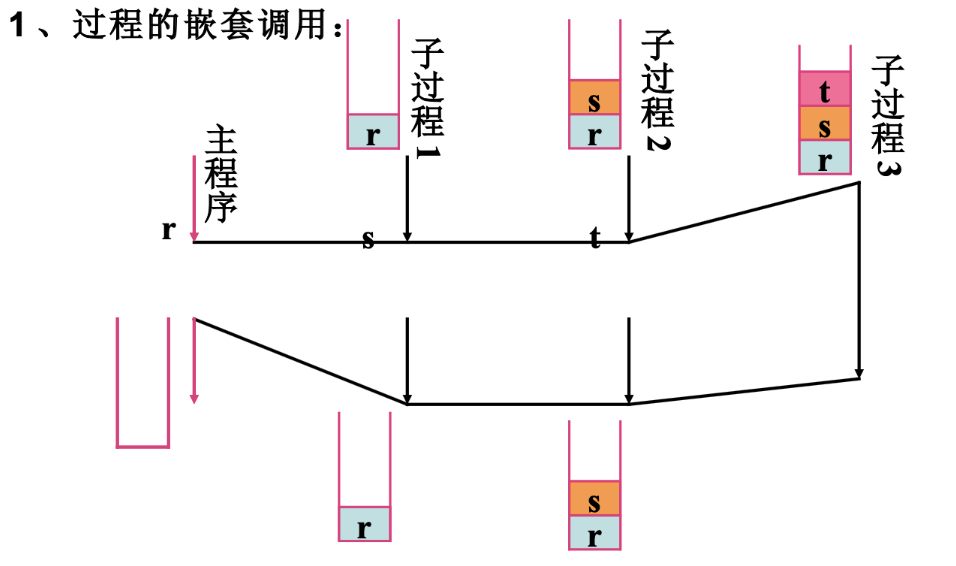
  • 过程嵌套调用，执行子过程1时要保存主程序r的地址，好执行完成子程序1后能通过主程序的地址r返回到主程序，子过程1的地址是s，子过程2的地址是t，。。。
  • 应用2：递归实现
    • 
    • 递推 到 print(w-1)==0 ，开始递归
    • 
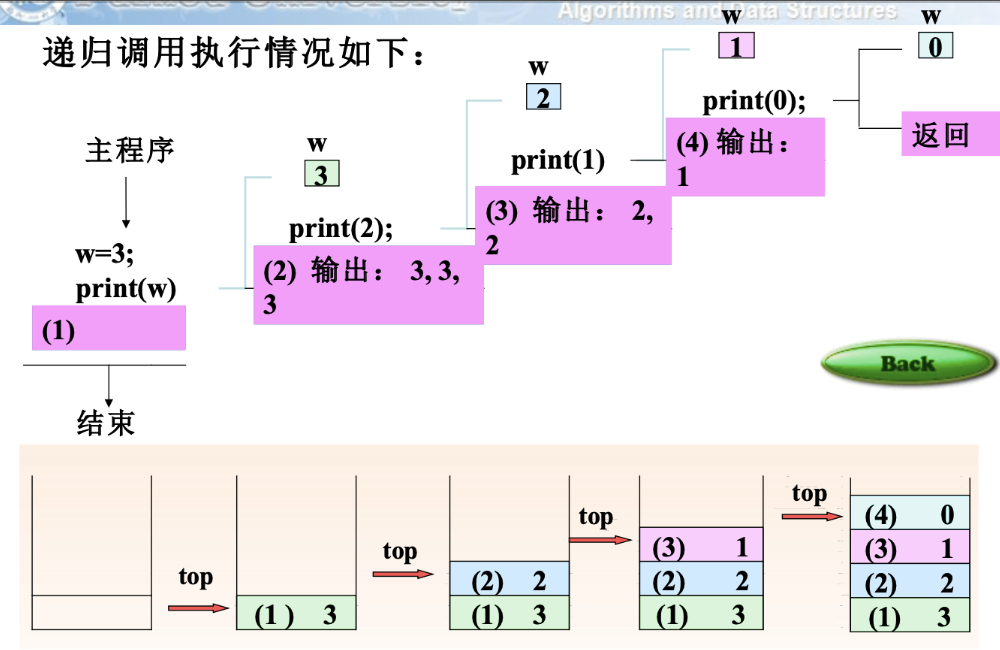
    • 使用技巧，计算出每层结果，然后叠放
  • 应用3:算数表达式
    • 
    • 界线符号 # ，用于标记表达式的结束
    • OP （operation）
    • 计算机将中缀式，转为后缀式，计算后缀式
    • 
    • 扫描到界限符#，将栈顶输出，最后的栈顶元素
    • 

第四章 队列

• First In First out，先进先出
• front 前面 rear 后面
• 队列是否满，尝试能否再次分配内存，如果可以就不满，分配了要free
• 返回队首队尾，先判断是否为空
• 队尾插入
  • 两个情况
    • 队为空，队首队尾都指向新节点
    • 队尾指向新节点
• 队首出队
  • 判空
  • 工作指针p帮助删除，x存储element，改动front
• 数组实现队列
  • 两种方法
    • 指向后移，越使用越少
    • 或移动元素，产生了循环数组
• 循环数组实现
  • 
  • +1 取余运算
  • 判空满
  • 
  • 少用一个元素，或设置一个变量记录
  • 
  • 
  • 指向队首前一个位置
• 队列的应用
  • 缓冲区
  • cpu调度队列，时间片
  • 最优电路布线
    • 栈实现的方式是深度优先，回溯最好就是用栈来实现
    • 用队列找到的方式一定是最短的，广度优先、
      • 长度为1的全部找出，长度为2的全部找出，。。。。。直到找到
      • 
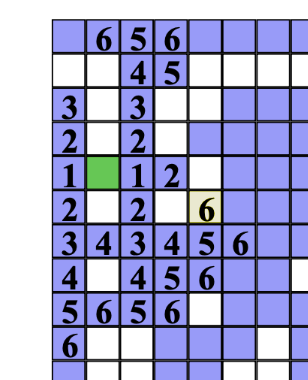
      • 6找小于6的，到5，5找小于5到。。。回溯回去
  • 划分子集问题
    • 
    • 2 8冲突。。。不存在冲突，还要尽可能少
    • 二维数组中 冲突关系表示为1
    • 
    • newr表示工作数组，newr是1到9的，工作数组，拷贝
    • 
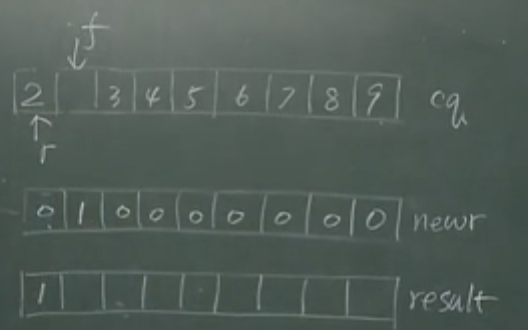
    • 1和2冲突，将2插入到队尾
    • result的1中的1表示第一组，3是和1一组的，在result的【4】位放1，表示和1一组，跟3冲突的再加入newr
    • 第一轮筛选结束，组数加一， 重新生成newr，为2的冲突列表
    • 

第五章 排序

• 两种解决机制
  • 比较运算
    • 冒泡、插入、选择 属于简单排序算法
    • 快速 、合并 渐进最优
  • 数字和地址计算
    • 桶排序
    • 计数排序
    • 能达到有前提条件的线性时间
• 排序问题如何解决
  • n个元素，每个元素是一条记录
    • 每条记录包含若干个数据域，必定有一个数据域，能符合线性序关系的，作为排序的依据，称为关键字域，值称为元素键值，剩下的域称为这个元素的卫星数据
    • node1{sum=10，course=20,course1=30…}
    • node2{sum=10，course=20,course1=30…}
    • node3{sum=10，course=20,course1=30…}
    • 键值为sum，根据键值排序，其他的course称为这个键值的卫星域
    • node为记录，一条记录有若干个数据域
    • 根据键值排序，并且根据排序移动卫星数据
    • 键值相等的元素没有特别的要求
• 基于比较的排序算法，时间下界是nlogn
• 数字和地址计算作为主要运算，桶，计数，线性速度
• 度量性能
  • 算法步数
  • 比较次数
  • 比较不多，元素大，移动困难耗时

简单排序

冒泡

• n为底，0为顶，自底向上，相邻元素比较，重的下落，轻的向上
• 
• 
• O(n^2)

插入

• 扩充有序序列，从无序序列，插入有序序列
• 插入元素，挨个比较有序序列中的元素，有序序列从1个扩充到n个
• 
• 默认第一位有序
• 最坏，完全逆序，O(n^2)，完全有序，移动操作为0，无操作可线性时间

选择

• 找出最小放置，i缩小，找n遍
• 每次到交换和比较次数固定
• n^2
• 不稳定

快速排序

• 分而治之，选一个基准元素，将其他元素分为左右部分，左右部分依法分解
• 
• 关键看如何分解
• 
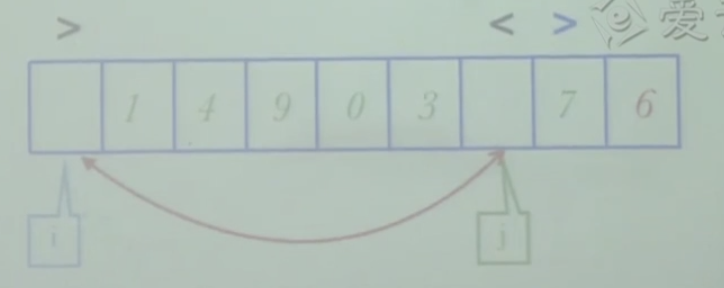
• 当左右元素都不对时，才交换左右元素，i 和 j 交叉，表示处理完成，
• 
• i 和 j 已经交叉，错位，i此时指向的是比6大的元素，所以跟i进行交换
• 
• 第一个while，i 右移 ，第二个 while ，j 左移
• 时间复杂度
  • 分解算法，分解算法基本是线性的，每一次都能对半分 O(nlogn)，完全逆序，每次都选最后一个为基准元素，没分好都是单边的,划分为n-1个和1个，O(n^2)
• 改进
  • 改进成 小于 等于基准 大于 三划分模式，原来是 小于等于 基准 大于等于
    • i 和 j 向中间移动时，遇到等于基准元素的，放在两端，当x为基准元素分解完成后，放到中间，再把两端的同基准元素相同的元素放在中间基准元素的两端
    • 
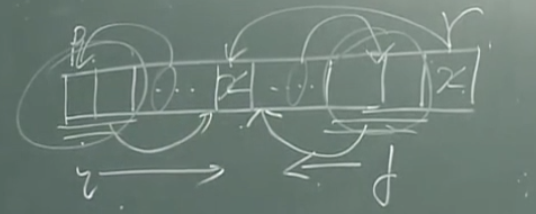
    • 可以改进有大量键值相等的元素，如果元素都不相等，但起码不会不会降低效率
  • 小规模数组，也要开辟栈，改进方法就直接不使用快速排序，使用简单排序
    • 小规模数组在5-25之间
  • 或不使用递归算法
    • 记录元素数组下标，用堆栈结构，保存划分子数组的起至下标
  • 随机选出基准元素
  • 三数取中，最右，最左，中间，三数中，选出一个，在中间作为基准元素
    • 
    • 基准元素还是放在r-1，最大元素方法在r，最小元素放在left，left ，r不参加分解，但是参加递归

合并排序

• 分解 、递归求解、 合并
• 分解的极限，每一个子序列只有一个元素，无法再分解，
• 合并时要使子序列有序
• 和快速的区别是合并和分解的方法不一样
• 
• b数组用来存放临时子序列
• [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-rvTFOqMF-1629271689864)(https://gitee.com/haoyunlwh/Typoraimage/raw/master/img/20210302112628.png)]
• 最好最坏都是O(nlogn)
• 渐进最优，非就地排序算法，因为增加了b数组作为辅助，大小为n
• 合并算法改进
  • 每次都要从b拷贝会a，消除拷贝运算，将b数组合并回a，ab数组交替使用，初始让ab两数组大小一样，本次以a数组作为原数组，b数组作为目标数组，下次以b数组作为原数组，a数组作为目标数组，交替使用 、
  • 不使用递归
    • 划分两个元素的子序列，四个元素的，八个元素的，直到最后完整的，直接不需要分解过程
    • 称为自底向上的合并排序算法，双层for，边界处理技巧
    • 
  • 自然合并
    • 改进输入序列，初始数组a通常存在长度大于1的有序子数组，扫描出已经有序的子数组段，将相邻的子数组段两两合并，构成更大的子数组段，来进行自底向上的合并排序
  • 链表排序
    • 主要问题在划分阶段，0 ---- n-1问题
    • 多使用两个指针，c b，c 指针步进值为1，b步进值为2，b到尾，c刚好到一半
    • 
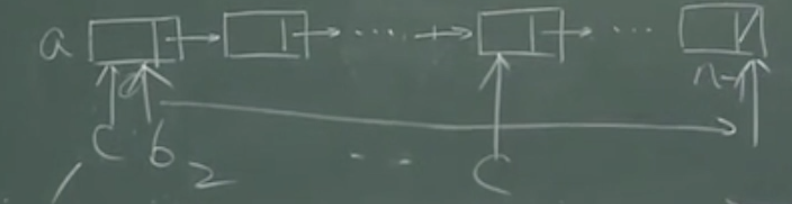
    • 如果不使用 自顶向下的方法 ，使用自底向上
    • 将元素打散，放入队列，队首取两个元素，合并之后放入队尾，一直循环到只剩下一个元素为止
      • 

桶排序

• 前提条件是，输入的取值在有限的确定的范围内
• n个元素分m个类，线性扫描，m个桶，m为 0---->m-1, m个桶串成一张表
• 
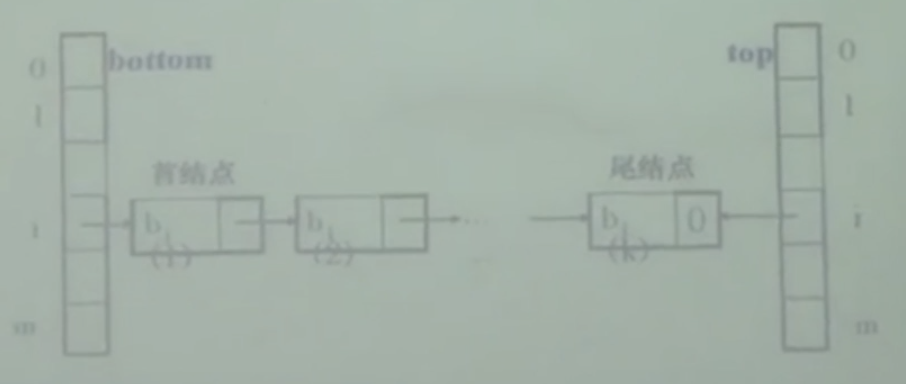
• bottom 底部，存放b链表的每个桶的桶底，top 存放每个桶 桶顶，用于串接每个桶，跳过空桶，
• O（n+m）
• 思想理解
  • 一共有三个数组，原数组a，数组bottom，和top，原数组a是一个链表，数组b和数组t是存储链表节点的数组，b和t初始链不相连，算法思想是，线性排序的的前提是元素关键字的需要在设定的范围m内，以链表节点为元素的数组 b和t以m为长度，b数组的每个节点都可以延伸为一个链表，输入的元素与b与t的下标相同，数字相同的一类数据存储在相同的下标之内，数相同的元素在b中形成一个链，链头存储在b中呢，链尾存储在 t 中，这样如果有m种元素将会形成m条链，最后将m条链首位相接，形成一条链，a链表头尾指针链接好，返回a链头指针，完成排序

计数排序

• 非就地排序，借助其他数组，
• c[ i ]中存放的是a中键值等于 i 的元素个数
• 

二叉树

• 每个节点的度数最大为2的不一定是二叉树
• 高度有h，至少有h+1个节点
• 满二叉树，最多2^(h-1) +1 高度最小
• 近似满二叉树，层序遍历有序的

顺序存储

• 左儿子是父节点，2n，右儿子是父节点的2n+1
• 非 近似满二叉树，容易浪费空间
• 结点度表示节点方法，表达四个状态用0–3来表示，
  • 0表示没有节点
  • 1表示只有左儿子
  • 2表示只有右儿子
  • 3表示左右儿子都有

指针实现

• 非递归实现就使用栈

• 层序遍历使用对队列，顺序为中左右、

• 测算树高度，左右子树分别递归叠加hl和hr，选出最大的h，+1，+1为根

• 线索二叉树

  • 利用空指针指向前驱或后继节点
  • 增加标志来标记出，是普通指针还是线索指向
    • 左线索，右线索
    • 
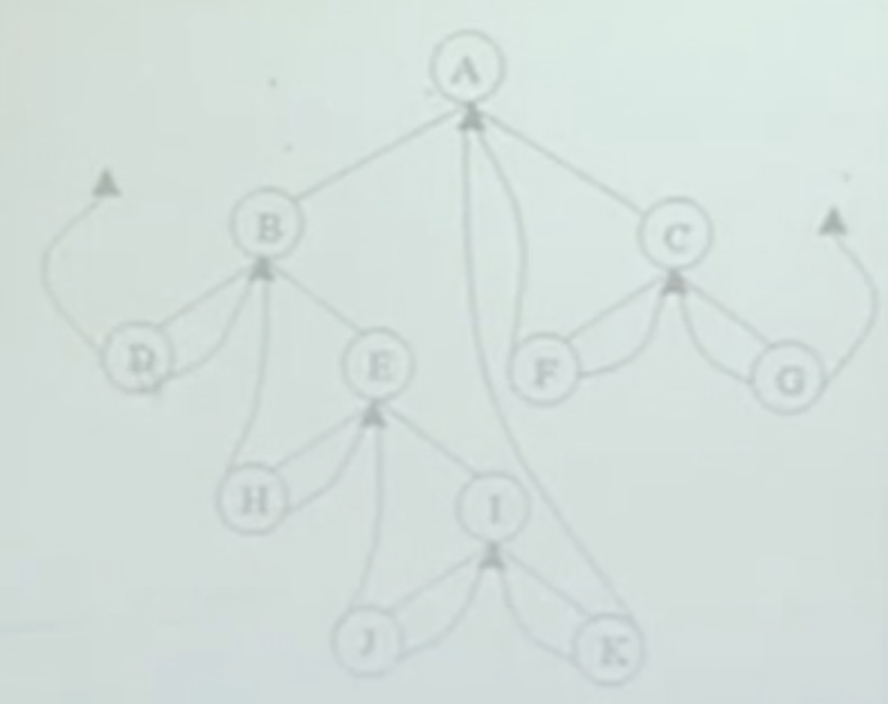
    • 这是一个中序遍历的二叉树，D为遍历的第一个节点，D作为遍历的第一个节点，而且是叶子节点，两个指针都空出来了，左指针应该指向前驱节点，但D是第一个遍历的节点，所以前驱节点为空，后续节点为B，D->R指向B
    • 适用于要频繁找前驱节点和后继节点，时间复杂度为O（h）

• 应用举例 衰减

  • 用后序遍历计算值，超过容许值的都防治一个增强装置，计算一边就能得出是最少的

图

• 图（graph）
• 完全图，任意两个顶点都有一条边，且只有一条边，n个顶点有，n（n-1）/2 条边
• 关联，u v之间有条无向边，称为相互邻接点， 相邻接，关联，有向边
• 顶点度，顶点的个数n等于每个顶点的度数相加除2
• 子图，表示时，加 ` ,顶点集是子集边集也是子集
• 路，根据是有向图还是无向图，也分有向路无向路
• 简单路，起点和终点不相同，简单的简单路经，和回路相反
• 有根图，从一个顶点能到图中的所有顶点
• 强连通，专门对于有向图而言的，任意两个顶点都有到达的路经，路经包裹直接连接，也包括间接到达，只是之间存在路经，称为强连通图
• 
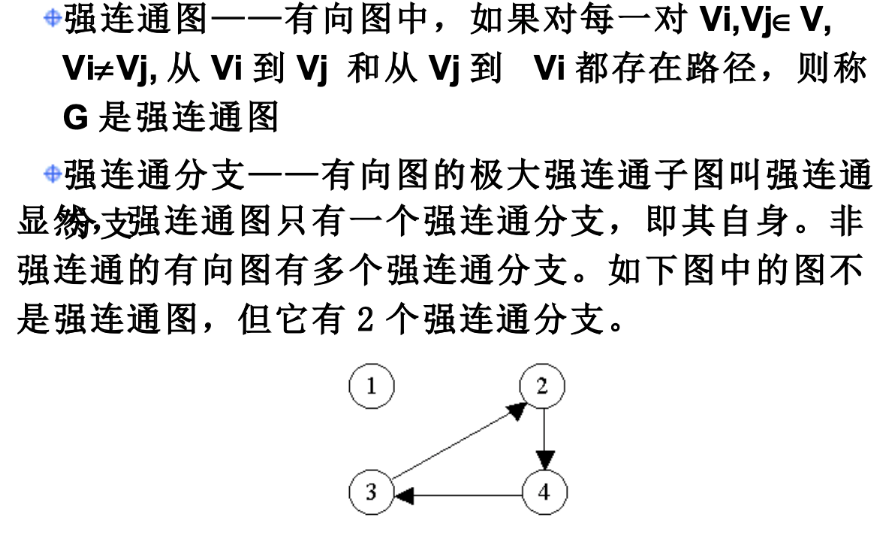
• 赋权的有向和无向图都可以称为网络
• exist 存在
• edges 边
• vertices 顶点
• degree 度
• outDegree 出度
• 紧缩邻接表，将相邻的顶点排在一起，每个顶点在一个数组中各有一个区间，用来存放相邻的顶点，用另一个数组存放顶点的起始位置
• [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Wdde4yFK-1629271689879)(…/…/…/Library/Application Support/typora-user-images/image-20210305213927838.png)]

邻接矩阵实现赋权有向图

• 有些从1开始n结束，初始化0行0列不使用
• 可自定义NoEdge 无边标记
• 添加边函数，不起覆盖作用，因为边总数e要增加
• 计算出度入度遍历分别遍历行和列 统计 ！=NoEdge数量

邻接矩阵实现赋权无向图

• 有向图为基础，两条有向边来实现无向边
• 在不更改数据结构的基础上，以两次操作实现无向图结构

邻接矩阵实现有向图

• 在赋权有向图的基础上，不使用权，关联顶点用1和0表示

邻接表实现有向图

• node顶点，和存放node顶点数组
• adjacency 邻接表 adj

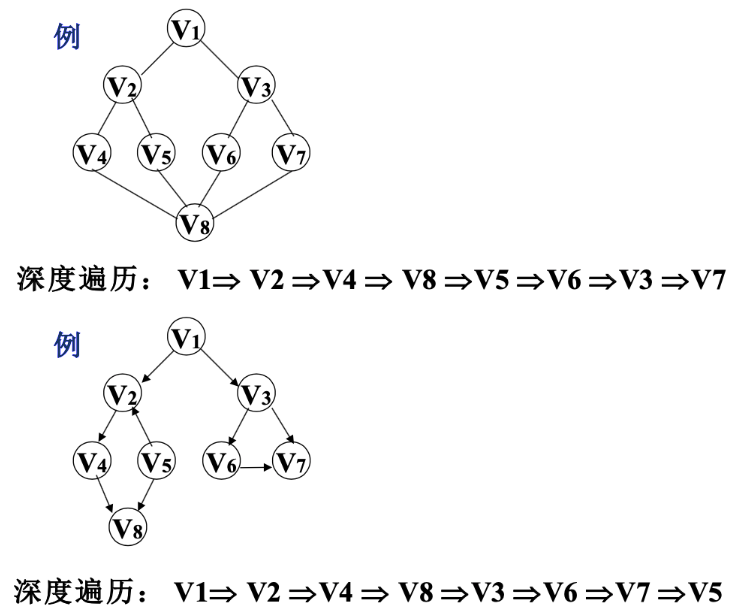
图的遍历

广度优先

• 差别就是使用队列还是栈
• BFS(breadth-first search)
• 访问过的顶点进行标记，跟当前顶点关联的顶点，用队列存储

深度优先

• DFS（depth-first search）
• depth 深度
• 

Dijkstra单源最短路径

• S表示已经求出最短路径的顶点集合，初始时原点已经在S中
• V vertices集合就不用考虑源点s了，所以V集合为V-S ， V-S用T表示尚未确定最短路径的集合
• 
• 找到了从源点s到v2的最短路径，就把v2加入到S集合中，V集合中不再考虑v2的最短路径
• 用dist数组存放从源点s到vi顶点的长度，将dist的最小值加入S，从s到vi的路径一半两种选择，直接到达，或经过其他节点间接到达，但如果以第二种情况求出的特殊最短路径经过的顶点要在S集合中寻找
• 
• dist初始时原点s到vi有边可直达，dist[i]就为两点直连到权值，如果不行，就设置无穷大
• 初始化完成后
  • 先从dist中选择一个最小的，每次从dist选择出一个权值最小的顶点从T加入S，
  • 那些没有直接边的顶点加入到S后，就可能能通过S集合中的顶点间接的找到的与T集合中结点的边，
• 贪心算法保证正确性的两个性质
  • 题目中可能有多个最优解，但是贪心算法一定能求出一个最优解
  • 第一 贪心算法的要求是保证所有的权值都必须为正数
  • 第二 源点到Vi的值一定要是最短路径
  • 
  • 假设i到k走上面两条竖线的2路是最短路径，那就能证明 j 走2到 k 是最短路径
  • 如果j 到 k 还有路径3是比2更短的，那 i 到 k就直接不会走2
  • 由子问题求出较大问题，所以要保证每次求出的是最优解
• 如果有边的值是负值
  • 
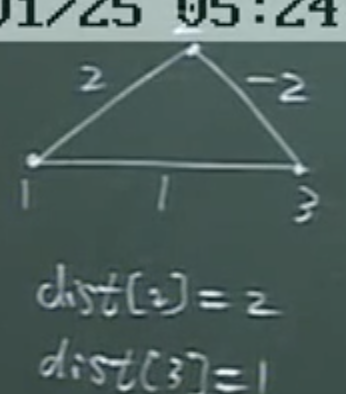
  • 源点为1开始，用Dijkstra算法就是错的，但也是可以求的，但是要考虑所有可能出现的路径，所有顶点都可能是1到3的中间顶点，可能经过n个顶点，所以要考虑所有顶点是否会存在路径，这就是Bellman-Ford 最短路径算法

Bellman-Ford 最短路径算法

• 所有顶点都作为中间顶点进行考虑，每个顶点的最短路径都考虑n个顶点
• 任何两个顶点都可能经过（n-1）条边
• 以边集作为两顶点之间可能经过的边
• 
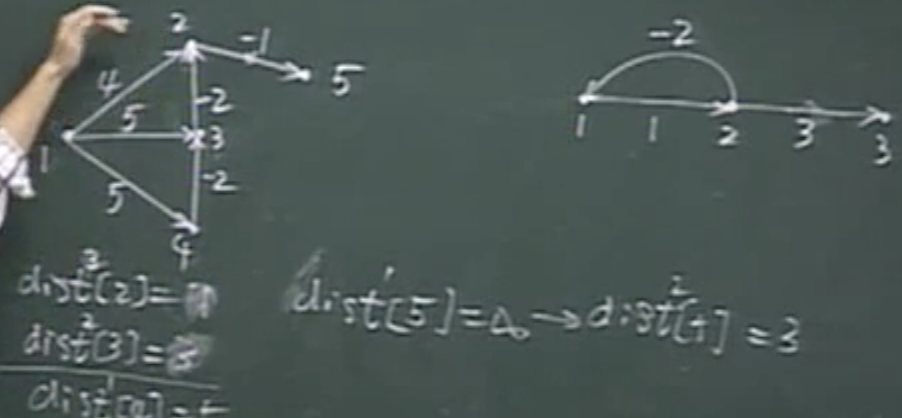
• dist的迭代不是对单个顶点的迭代，而是一次对n-1个顶点的最短路径进行迭代
  • dist1时 4、5、5、0
  • dist2时 3、3、5、3 dist迭代第二次时是考虑两条边的情况，u1通过u3到u2，u2更新路径，u1通过u2到达u5，长度为3
  • dist3时 1、3、5、2
  • dist4时 1、3、5、0
• 用邻接表来实现就是O（en）
• 用邻接矩阵来实现就是O（n^2）
• bellman ford算法要求
  • 负回环，第二张图，1-2，2回到1不断的回，导致2不断缩小，书中加入count来统计，是否超过n条
• 传递闭包 也可使用这种方式实现，只是证明任意两顶点是否可达的关系，每次增加节点考虑是否联通
• 如果有时间应该编程实现

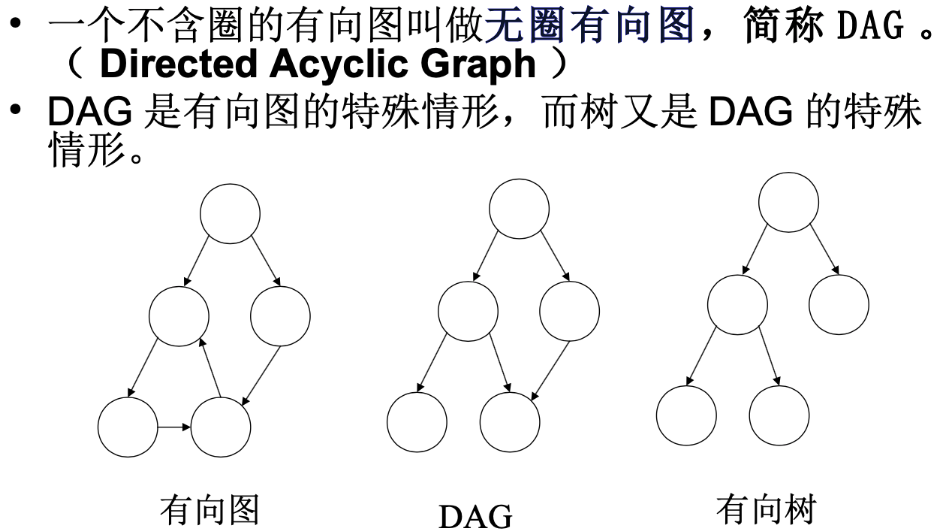
无圈有向图DAG

• Directed Acyclic Graph 定向 非循环 图
• 
• dag可以表示用来描述表达式
• 
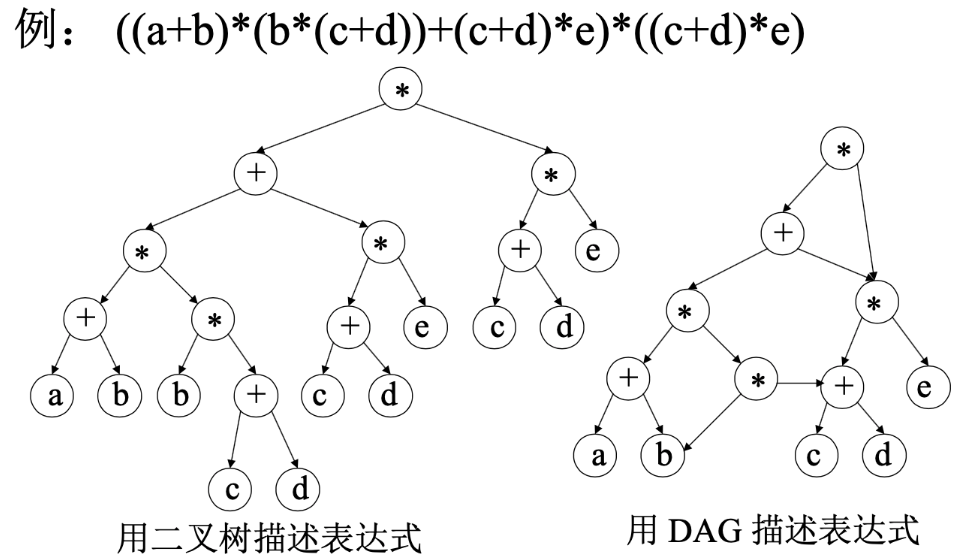
• 将公共的表达式合并，节省空间
• 
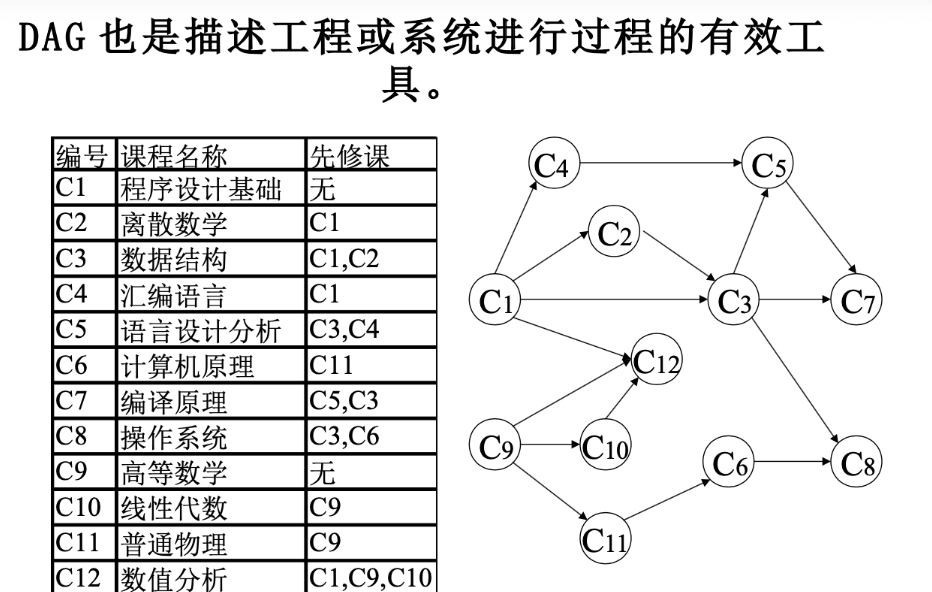
• 实际应用，用来表达先后次序
• 开课次序应该选择从无前驱节点的位置开始

拓扑排序

• 应该从无制约的顶点开始，就是入度为0的顶点开始
• 
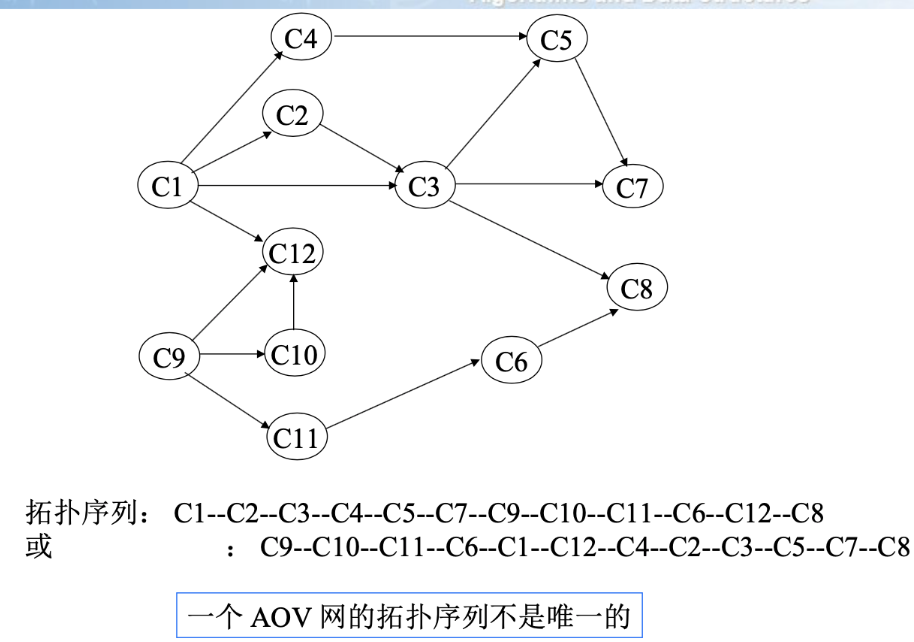
• 可以用栈或队列，入度为0的顶点入栈，栈非空，这个顶点出栈时将，这个顶点的出度的边都删除 ，并且修改与之相连的顶点的入度值，进行下一轮的入度为0的顶点入栈出栈
• 拓扑排序，逆向拓扑排序，
• 最优子结构性质，整体的最优解 包含 子结构的最优解
• 动态规划的思想就是用子结构的最优解求出整体的最优解

AOE关键路径

• 
• 顶点代表一个事件，在顶点之前的代表这些活动都已经结束，在顶点之后的代表活动都可以开始
• 
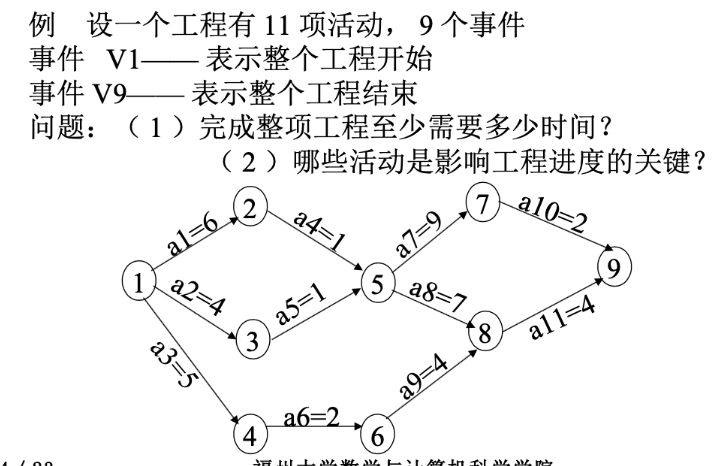
• 在完成9之前，前面的任务都必须完成
• 关键路径不能拖延
• 
• 找到 l(e) = e(i) 最早和最迟的开始时间

生成树

• n个顶点n-1条边，保证顶点联通，首先保证连通图，但不产生回路，生成树可能有多棵，最小生成树为长度最小的，但不一定唯一，
• 在n个顶点可设置n（n-1）/2条边，建立最小生成树之需要n-1条边
• 两个找最小生成树的算法，两个算法都是贪心算法，Prim算法，Krushal算法

Prim算法 谨慎

• 
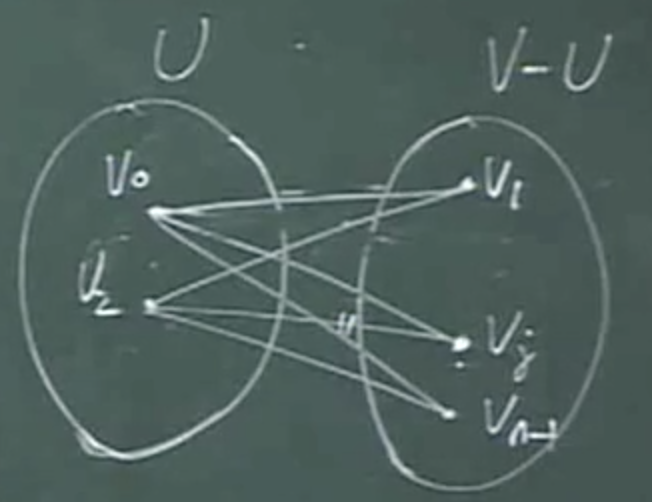
• V2原本在右侧，当（V0，V2）权值最小，将V2加入左侧，V0，V2与右侧相连的边集中寻找最小的边加入，加到n-1条边时最小生成树的边全部找到，左侧的已经找出的边已经构成了当前的最小生成树，最右边的顶点加入，是将未加入的顶点加入最小生成树，不会产生回路，并且每次找到的边也是最小的边，前面证明了最小的边一定在生成树之中
• 
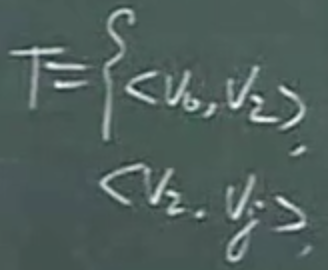
• 完成两次操作，最小生成树的边集合，

集合

• 成员同一类，不重复，
• 有时也可以相同，称为多重集合
• 原子具有线性序关系，称为有序集
• 并、差、交、异或等运算
• 向量实现比较费空间，但是实现简单

位向量实现集合

• 树上157页通过位置的0和1来表示元素是否在集合中存在，提供了两种思想，一种是直接n长度的数组来实现，元素对应下标，数组通过设置0或1的方式来表达原子在数组中存在，这种方法比较消耗内存，n就是元素有效范围，当n十分大时，数组的大小也为n，十分容易造成空间的浪费，在并交差等操作时间复杂度都为O(n)复杂度

• 书上介绍的方法是，选用unsigned short 类型在作为数组存储单元的类型，这种类型占用2个字节，即16位Bit，当bit位的1位到16位可以表示0-----15

• S->v[0]，这一个数组单元就能表达0-----15，共16位的数，S->v[1]能表示16—31，

• 主要思想就是x存储在哪一个区间，和计算出1的左移次数，存放在当前这个区间的第几位

• 存储在哪一个区间

  • ArrayIndex x>>4 //对16取整

• 存储在区间中的第几个位置

• BitMask 1<<(x&15) //相当于对x取余 %16

• #include <stdio.h>#include "stdlib.h"typedef struct  bitset *Set;typedef struct bitset {	int setsize;	int arraysize;	unsigned short *v;	}Bitset;Set SetInit(int size){	Set S = (Set)malloc(sizeof(Set));	S->setsize  =size;	S->arraysize  = (size+15)>>4;	S->v = (unsigned short *)malloc(size*sizeof(unsigned short));	for (int i=0;i<size;i++) {		S->v[i]=0;	}	return S;	}int ArrayIndex(int x){//	return x>>4;	return  x/16;	//十六个单位为一个区间	}unsigned short BitMask(int x){	//	return 1<<(x&15);	x %=16;		return 1<<x;	}void SetInsert(int x,Set S){//	if(x<0 || x>=S->setsize)return ;	unsigned short a;	int i,p;	a = BitMask(x);	i = ArrayIndex(x);	p = S->v[i] |= a;		}void SetDelete(int x,Set S){//	if(x<0 || x>=S->setsize)return ;	S->v[ArrayIndex(x)]  &= ~BitMask(x);}int SetMember(int x,Set S){	return S->v[ArrayIndex(x)]&BitMask(x);}int main(int argc, char *argv[]) {//	printf("%d\n",sizeof(unsigned short));	//16位	Set S = SetInit(10);	SetInsert(16, S);//	SetInsert(36, S);//	SetInsert(13, S);//	SetInsert(0, S);//	SetInsert(5, S);	//0为第一区间的第一位//	SetInsert(16, S);	//16为第二区间的第一位	//每一个区间都能存放16位	//	SetInsert(144, S);//	SetInsert(164, S);//	SetInsert(175, S);	printf("member :%d \n",SetMember(1,S));	SetInsert(3, S);//8//	SetInsert(2, S);//4//	SetInsert(2, S);//4	//12//	SetInsert(1, S);//2//	SetInsert(0, S);//1//	SetInsert(-1, S);//0//	SetInsert(-2, S);//0	//	SetDelete(9, S);//	SetDelete(4, S);	for (int i=0;i<10;i++) {		printf("%hu  ",S->v[i]);	}	printf("\n%d",1<<30);	}  
  

• 

• 和数因子，和数因子是从素数中产生的，最小的素数为2，m作为合数因子，从2开始，配合k+=m，删除合数因子的倍数，当m不断扩大时，如当m为5的时候，上一层的循环为4的时候，4已经被m为 2 的时候删除了，所以m走完素数2走素数3，跳过已经被删除的4直接走到5

• 

链表实现集合

• 就是普通单向链表结构
• 通过普通的比较来完成操作

散列表

• 符号表可以称为散列表查找，集合member 、insert、delete三种运算的冲向数据类型的专门名称称为符号表，查找十分高效
• 散列发生冲突时如何解决冲突
• 普通数组方式实现符号表只是无序存储，加入last，进行三种基本操作都是O(n)时间复杂度，直接淘汰
• 二分查找是logn时间

开散列

• 建立元素键值和对应存储位置之间建立联系关系 ，每个值都能通过计算得到一个唯一的存储位置值从而建立唯一一个联系，时间复杂度就能降低到O(1)
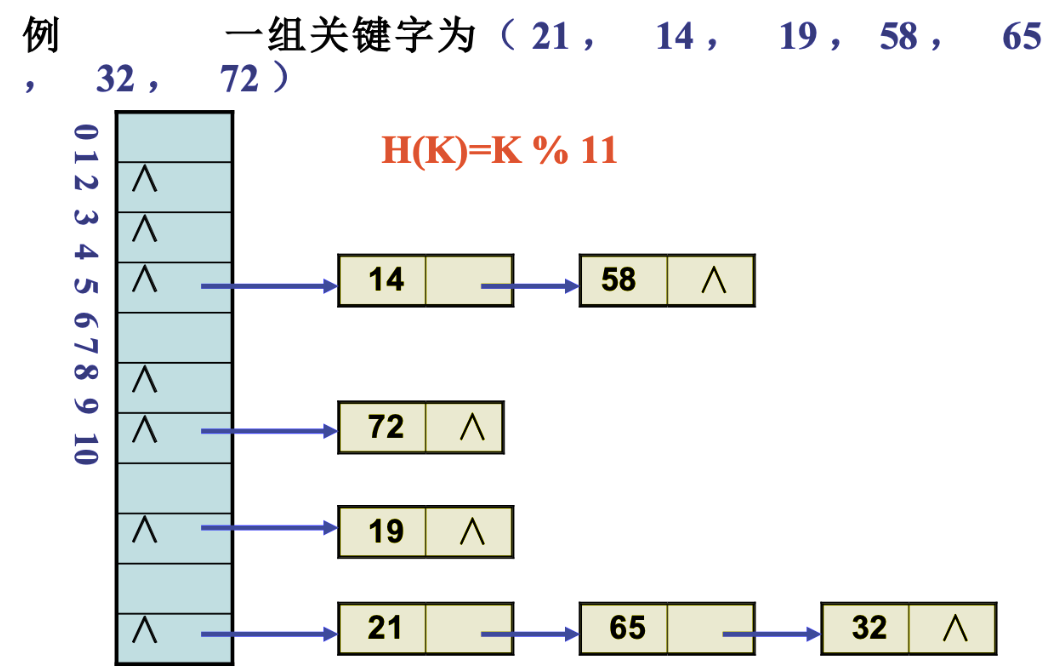
• 开散列主要思想
• 
• 使用的是桶的概念，3不直接存储元素而是像桶排序，每个存储位置都能延伸出一条链，每个单元都是一个桶，通过计算，将计算出相同key的元素放入同一个桶中
• 选取一个合适的key能让每个桶存放的元素均匀分布，最重要的就是构造散列函数
• 

闭散列

• 不使用桶的概念，直接存储在数组单元中，会产生冲突，如何解决冲突，相同的都是使用散列函数的构造
• 线性探测法处理冲突
  • 加入存储标记，标记已经存放的数组单元
  • 如果散列函数H（key）计算出的位置已经存放，就+1，向后探步，探步到尾巴要回到头部开始，和表长n取余
  • 要注意的是曾经存放过的位置的桶，元素被删除，不能直接设置为0，桶应该有三种状态，0为一直为空，1为满，2为曾经存放过，当此桶存放 a 为满时，插入这个位置的元素 i 向后探步，当这个 元素 a 被删除后，原 元素a的位置被删除，查找 i ，定位到a，就不会继续向后探步，所以需要增加一个新的状态2，表示曾经存放过，让key为a index的查找能向后探步查找
• 构造散列函数
  • 计算时间复杂度要低
  • 元素分布均匀
  • key%m m一般选取！=2 的素数
  • 有很多种，具体问题具体分析
  • 或者改进Delete操作，删除当前元素后，向后探步寻找，相同key但不再桶中向后探步的元素，放在桶中，找另外一个元素代替，
    • 这是用删除的效率换查找的效率

优先队列

字典

• 在集合的基础上寻找前驱后继节点
  • Predecessor 前驱运算
  • Successor 后继运算
  • Range （x,y）区间查询
  • min、insert、delete、member
• 寻找区间值
• 有序集

数组、链表实现

• 查找可以用二分法 logn
• 插入删除元素移动，保持有续集，O(n)
• 链表插入删除查找都慢不推荐

二叉搜索树

• 任何一个节点都大于左子树，小于右子树
• 相当于在链式存储中加入二分查找，查找效率为logn
• 中序遍历保证了有序性
• 为保证处理效率，尽量保证左右树高度相等
• 不插入相等的元素，如果按二叉搜素树插入相等的元素就在元素中加入计数使相同的元素不加入树中，只记录在节点中
• 插入操作
  • 查找定位插入
  • 不同的插入顺序得到的搜索可能也不同
  • 普通操作不能保证左右两颗树高度相等
  • 最坏情况就是单边树，最好情况两树高度相等
• 删除操作
  • 删除跟节点，选 右儿子的最左子树 或 左儿子的最右子树 替换
    • 中序遍历 根节点的 前继 结点在左子树 的最右子树 ，后继是右子树的最左结点
  • 几种情况
    • 为叶节点，直接删除
    • 单子树，只有一个儿子，区分左右，选一个代替
    • 左右子树非空
      • 可以选前驱节点也可以选后继节点，进行交换删除，替换那个结点由设置决定
      • 左子树最右节点，或右子树最左结点
    • AVL树还要加入平衡运算
    • 最好情况 logn 最坏On 平均logn
• Predecessor 前驱结点 Successor 后继结点
  • 先查找x
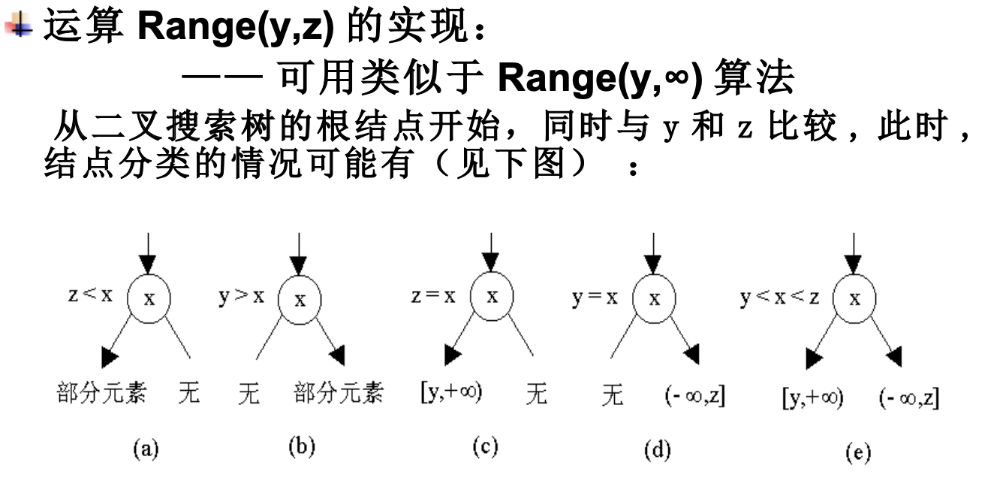
• range(y,z)区间查询
  • 先找x所有的后继节点，包含条件是y的前驱条件，反过来也可以
  • 查找的效率为logn 区间如果有r个就是 r*logn
  • 如果使用线索二叉树，找前驱和后继节点就只要常数时间，O（r+logn）
  • range改进
    • 半无限查询区域，y到z，y的后继节点都会比y大，所以y到正无穷区间
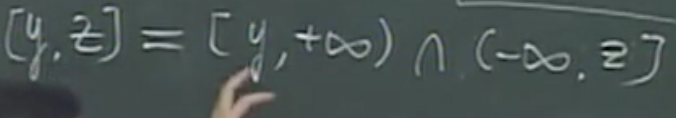
    • 负无穷到z
    • 

AVL树

• Rebalance
• 书本没涉及平衡二叉树

字典

• 用表格的方式统计数据出现的频率
• 计数排序、二叉搜索树 给元素加入计数标志 中序遍历 插入速度会提高，平衡二叉树又会更快

优先队列

• 每个元素有优先级

• 优先级可能重复

• 优先级高低由自己定义，数值大或数值小的作为高优先级

• DeleteMin删除优先级最小的元素，主要关心优先级最小的元素

• 用树和字典实现优先队列都不是最高的，优先队列最关注的操作就是找优先级最高的元素

• 最小和最大堆，或称极小或极大优先级树，根节点小于左右子树，根节点是所有元素中最小的

• 堆实现

• 满足优先级树又满足近似满二叉树

• 近似满二叉树能用顺序存储，父子关系通过下标实现，

• 插入操作

  • 叶子节点位置插入与父节点进行比较，一路向上比较

• 删除操作

  • root节点与层序最后一个节点交换，最小的元素根就已经换到层序最下端，删除，
  • 大的数位于顶层，向下比较，选取左右树中最小的交换，直到找到正确位置
  • 插入删除时间复杂度都是On

• 用堆进行排序

  • 和选择排序相近

  • 只是全部元素插入删除就能得到有序效率为O(nlogn)，但这只是全部元素删除的时间复杂度，还需要加上建堆的时间

  • 

  • k为当前节点，m为底部位置，

  • 建立初始堆

    • 从下向上调整

    • 

    • 

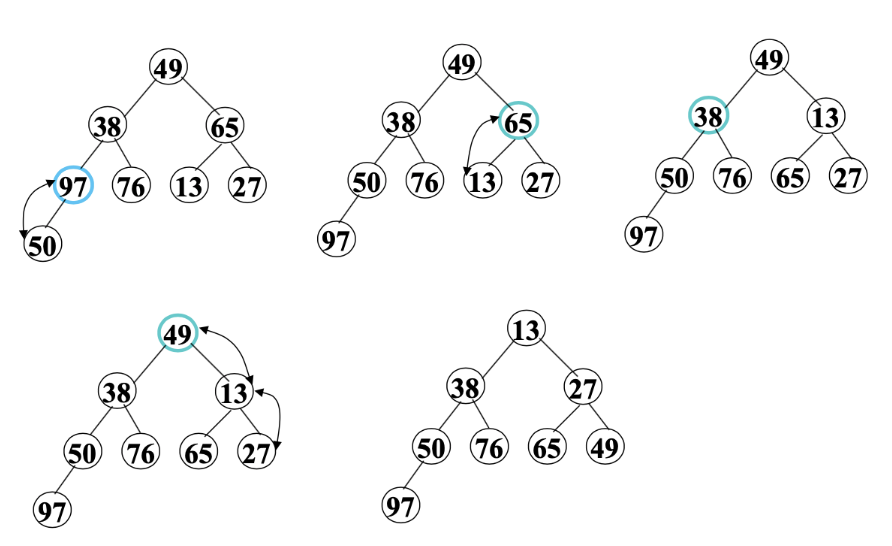
    • n/2开始，一个for循环就能n/2的位置从下向上构建完成堆，调整每一个节点所在的子树调整为一个堆，第二个for循环意义不明，

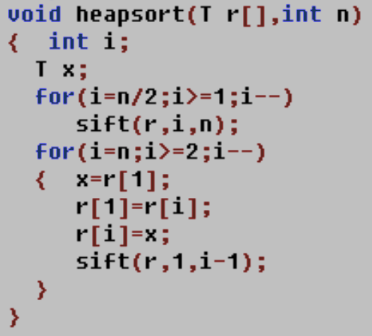
    • #include <stdio.h>int sift(int r[],int k,int m){	int i,j;	int x;	i = k;	x = r[i];	j=2*i;	while (j<=m) {		if((j<m)&&(r[j]>r[j+1]))j++;		if(x>r[j]){			r[i]=r[j];			i=j;			j*=2;					}else {			break;					}	}	r[i]=x;	}void heapsort(int r[],int n){	int i;	int x;	for (i=n/2;i>=1;i--) {		sift(r, i, n);			}//	for (i = n;i>=2;i++) {//		x = r[1];//		r[1] = r[i];//		r[i]=x;//		sift(r, 1, i-1);//		//	}}int main(int argc, char *argv[]) {	int r[9]={0,49,38,65,97,76,13,27,50};	heapsort(r,9);	for (int i=1;i<9;i++) {		printf("%d ",r[i]);	}}
      

可并优先队列

• 逐个插入效率较慢，使用左偏树概念
  • 合并时间不超过logn
  • 左偏高树
    • 任意一个子树，左子树的高度都大于右子树的高度
    • 递归定义
  • 左偏重树
    • 任意。。。左边重量都大于。。

哈夫曼树Huffman

• 带权路径长度最短的树
• 压缩算法
• 一个编码是另一个编码的前缀，就无法解码，从跟节点走到也节点作为一个编码，就不会产生为前缀的问题，证明使用不等码也是可以实现编码
• 不等长编码还压缩了编码长度
• 
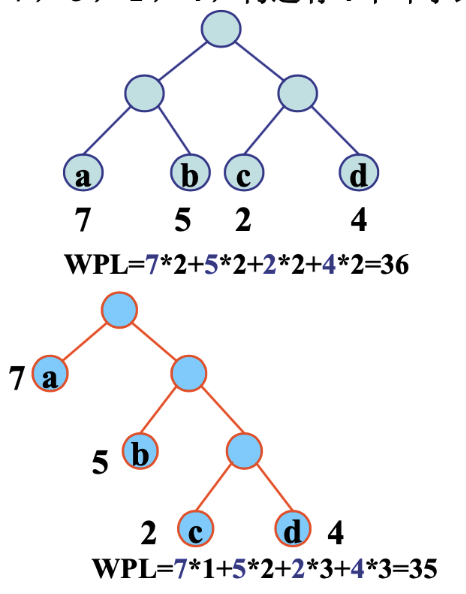
• 选出两个权值最小的合并成新的树，产生的树合并入森林
• 从每次取数组中两个最小值的性质可以使用优先队列，
• 没有度为1的节点，每次都是通过两个节点合并成一个节点，所以没有度为1的节点
• Huffman tree可以为
  • 
  • Huffman数没有度为1度的节点
• 普通树的节点树为 度0的节点数 + 度1的节点数 + 度2的节点树

并查集

• 以集合为基础
• 要频繁查找元素属于某一个集合，得到第几个集合，实现合并和查找的运算
• k个集合不相交
• 集合名字由root节点表示
• 属于同一个集合的就不能合并

小程序练题收集

• //注意指针叠加int main(int argc, char *argv[]) {	int a[]={2,4,6,8,10,12,14};	int *p;	p = a+4;	printf("%d\n",*p++);//10	printf("%d\n",(*p)++);//12	printf("%d\n",*p);//13	printf("%d,%d\n",p[-2],*(a+4));//8,10}
  

• //正负数reverse反转int reverse(int n){	int sign=1,m;	if(n<0){		sign =-1;	}	n = (n>=0?n:-n);	m=n%10;	while (n>=10) {		n = n/10;		m = m*10+n%10;			}	return sign*m;}
  

数据结构注意点

• 存储结构

  • 
  • 线性表既可以用数组实现，也可以用链表实现
    • 数组实现：无力空间在物理层面都是连续的，所以使用的是顺序存储结构，数组实现有下标，可以直接定位存储单元，所以使用的顺序存储结构存取方式是随机存取
    • 链表实现，逻辑上是连续的，但物理上是不连续的存储单元，存储结构是随取存储结构，存取方式是顺序存储，插入删除查找都需要遍历链表来实现。
    • 注意存储结构，和存取方式的区别

• 二分查找

  • 

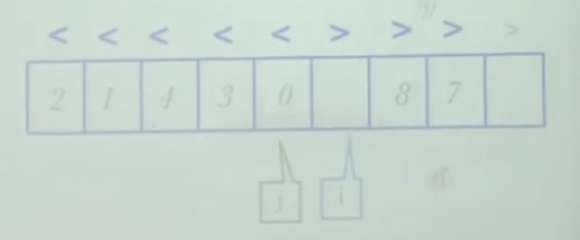
  • int Binary_Search(int* a, int size, int val){	int pos = -1;//pos返回查找到的值的位置	if (a == nullptr || size < 1)//数组合法性检查	{		return pos;	}	int left = 0;	int right = size - 1;	while (left <= right)//当左端元素位置不等于右边元素位置时反复查找	{		int mid = (left + right) / 2;		if (val < a[mid])//若所查找值小于中间值，在前半部分查找		{			right = mid - 1;		}		else if (val > a[mid])//若所查找值大于中间值在后半部分查找		{			left = mid + 1;		}		else		{						pos = mid;//若已找到则终止循环			break;		}	}		return pos;//返回查找到的值所在位置}	
    

  • 范围从0------ size-1

  • 先判断array [2]，20，缩小再判断，25

• 二叉树非空域

  • 
  • 一个节点有两个域，分别指向左右子树，注意分析题型

• 单链表上溢

  • 
  • 空间分配完毕，也会发生上溢

• 算法四个性质

  • 输入
  • 输出
  • 确定性
  • 有限性、有穷性

• 循环队列优点

  • 
  • 普通数组实现队列，执行删除操作就要将队列向前移动，循环队列利用两个下标实现元素不用移动
  • 判空 front==rear
  • 判满（rear+1）%maxsize == front
  • 删除要判空，插入要判满

• 基数排序

  • #include <stdio.h>#include "stdlib.h"#define RADIX 10void RadisSort(int array[],int l,int r){	int pow=1,max=1;			//申请临时数组b	int * b = (int*)malloc(sizeof(int)*(r+1));			//找出max，max的位数决定需要进行几次的排序  //算法思路，先根据个位数排序，然后根据十位数排序，然后。。  //排序的次数根据max的位数决定  	for (int i=l;i<r;i++) {		max<array[i]?max=array[i]:max;			}  //pow 初始为1，第二轮变成pow会变为10，RADIX决定的是进制，如果是10进制就是10，八进制就是8	while (max/pow) {		//重制count	    //根据count的统计来，来确定根据当前排序位应该处于什么位置		int count[RADIX]={0};			int i;    		//统计array元素的位数		for ( i=l;i<r;i++) {			int k;			k = array[i]/pow%RADIX;			count[k]++;		}				//计算前缀和    //位数有相同的时候，进行增加，到时将元素放回去的时候要--		for ( i=1;i<RADIX;i++) {			count[i]+=count[i-1];					}		//临时存放到b中    //count需要--，以防相同位数将位置叉开		for ( i=r-1;i>=l;i--) {			b[--count[array[i]/pow%RADIX]]=array[i];					}    //写会array中		for ( i=l;i<r;i++) {			array[i]=b[i];					}    //进制		pow *=RADIX;			}	free(b);	//释放b临时数组	}void printArray(int array[],int l,int r){	printf("\n");	printf("\n");	for (int i=l;i<r;i++) {		printf("%4d",array[i]);	}	printf("\n");	printf("\n");}int main(int argc, char *argv[]) {	int array[] ={39,457,657,39,436,720,355};	int i=0;	int size  = sizeof(array) /sizeof(int);	RadisSort(array, 0, size);	printArray(array, 0, size);}
    

• 数据的逻辑关系，数据的逻辑结构划分为 4类

  • 
  • 逻辑结构
    • 集合结构，是否属于同一个集合的关系
    • 线性结构，一对一关系
    • 树形结构，一对多
    • 图形结构，多对多
  • 存储结构
    • 顺序、链式存储
    • 索引存储
      • 除建立存储结点外，还附加索引表来标识结点的地址
    • 散列存储
      • 根据节点关键字直接计算出该节点的存储地址
    • 一种数据结构可以表示成一种或多个存储结构
  • 逻辑结构用于设计算法，存储结构（物理结构）用于算法编码实现，逻辑结构与存储结构没有必然的联系，存取结构又是对逻辑结构中数据的存取
  • 数据结构中，一般分为线性结构和非线性结构

• 地址计算

  • 
  • 相差个数*单元素大小+收地址

• 算法五特性

  • 输入、输出、
  • 有穷性
    • 不会无限循环
  • 确定性
    • 每一步不产生二义性
  • 可行性
    • 每一步都可行，在能够执行有限次数完

• 算法复杂度

  • [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LYir2Bmq-1629271689933)(https://gitee.com/haoyunlwh/Typoraimage/raw/master/img/20210313170119.png)]

• 排序受挫经验

  • 基数排序

    • 忘记计算前缀和
    • 忘记禁卫 pow * = radix；
    • 释放临时数组
    • –count

  • 快速排序

    • left和right的起始位置，因为是–i ，–j开始的
    • 要根据使用的是最左元素还是最右元素选择i和j开始和的位置
    • 使用最左元素作为基准，交换j位置，返回j
    • 使用最右元素作为基准，交换i位置，返回i

  • 冒泡排序

    • 使用swap交换，注意传值引用和转地址应用，最好使用define swap
    • i =1向后，j=i向前
    • j和j-1比较

  • 选择排序

    • 一般两种方式，min记录值交换，或记录min下标交换

    • void selectSort(int array[] ,int length){		int i,j;	for ( i=0;i<length;i++) {		int min =i;				for ( j=i;j<length;j++) {			if (array[min]>array[j]) {				min =j;							}				}		swap(array[i], array[min]);	}}void selectS(int array[] ,int length){		int i,j;	for ( i=0;i<length;i++) {		int min =array[i];				for ( j=i;j<length;j++) {			if (min>array[j]) {				min =array[j];				swap(array[i], array[j]);							}				}			}}
      

  • 插入排序

    • 两种方式，分开交换，一次性交换

    • 分开交换交换次数少

    • 一次性交换交换次数多

    • 两者比较次数不变

    • void insertSort(int *array ,int length){	int j;		for (int i=1;i<length;i++) {		int temp = array[i];				for ( j=i;temp<array[j-1]&&j>0;j--) {				array[j]=array[j-1]; 		}		array[j] = temp;			}}void Insert(int *array ,int length){	int j;		for (int i=1;i<length;i++) {				for (int j=i;j>0;j--) {			if (array[j]<array[j-1]) {				swap(array[j], array[j-1]);			}		}			}}
      

  • 归并排序

    • 注意左右元素边界，什么时候后使用<=,要将边界元素包含
    • 产生过错误copy没复制完全

总结数据结构书中思想技巧

引论

• 注意设置递归结束条件，多看递归式
• 典型问题：
  • Fibonacci数列
    • While 自底向上方法 1 2位初始化为1
    • 递归法，自顶向下 ，结束条件 n=0 ret 1
    • While数组滚动计数，之需要两个元素，根据–n，n&1，存放在0位和1为，【0】和【1】，滚动叠加，
  • 连续整数和问题
    • 6=1+2+3
    • 左右各一个标记，和大时，减去左边，和小时增加右边

表

• 数组实现
  • 插入删除要移动元素
• 链表实现
  • 插入删除判空满
• 间接寻址
  • 不需要移动较大元素只要移动指针
  • 数组为基础，插入删除同样移动数组中的指针
• 游标实现
  • 手动实现单元释放
• 循环链表
  • 注意有是否加入 表头节点
  • 从last开始还是从head开始
• 双链表
  • 注意是否加入表头节点
  • 插入删除要进行的修改指针操作，左右指向
• 应用举例
  • 环形淘汰，隔开多少人就淘汰一个，最后剩一个
    • 两层for ，For从1–>n,for（j=i——m）
  • reverse
    • 两头向中交换
  • 两数组合并
    • 交替插入，可加入判断大小就变成有序数组合并，
    • 剩余元素处理
  • 奇数分割
    • 交替输入给两个数组，
  • 链表reverse
    • 使用工作指针向后，挨个将节点指向前一个节点，最后一个节点作为新的头
    • 单循环链表同理
    • 双循环链表，逐个交换每个节点的左右指针
  • 链表交替合并
    • 交替合并，处理剩余元素
    • 加入判断，变成有序表合并
    • 单循环，双循环链表同理
  • 条形轮廓图41页

栈

• 数组实现

  • 新元素存放在top+1位置，top初始-1
  • 入栈++top，出栈top–，注意顺序

• 指针实现

  • 入栈，在队首插入

• 应用举例

  • stackSplit 分两个栈，上下部分

    • 数组直接切
    • 指针实现
      • S1切分成S1和S2
      • 遍历测算数组长度/2
      • S1，top向下不删除元素，中间位置作为S1top位，源top位置作为S2top，切开后S1->top=0

  • combine 合并，顺序不变

    • 数组接上，改动top
    • 链表实现
      • S2向下寻找栈底，链接到S1栈顶，修改S1栈顶，S2栈关闭

  • 括号匹配

    • 左括号入栈，来右括号出栈
    • 数组空，栈不空，多左括号
    • 来右括号，栈空，多右括号

  • 计算后缀表达式

    • 处理数字
      • 遇到数字就入栈，从表达式到入栈的元素还要经过计算
      • 后缀式数字在前符号在后
      • 26 90+
      • 26和90中间用空格间隔空格，输入数组中占五个单位，单只表示两个数，要将2和6合并成26
      • 如果是数字 while循环pop和push操作叠加数字，x = pop（s），push（ 10*x+(a[ i++ ] - ‘0’) ,S）
      • 顺序2入栈，while ，2出栈，2*10+6入栈，空格的时候i直接++跳过
    • 处理符号，pop两次，计算后，入栈
    • 最后得出后缀表达式值

  • 两个栈共享一个数组

    • 两头向中

  • 多个栈使用游标实现记录栈顶栈底，可分配可分配空

  • findmin栈O1时间找到栈中最小元素

    • 加入辅助栈，minstack 的 top始终是最喜爱哦元素，小于minstack就入min顶，不小于入普通栈
    • 出栈stack普通栈top等于mintop时，同时出，否则只之处普通栈，保证min栈顶一直都是最小的

  • 单词反转reverse

    • hello world 反转为olleh dlrow，以单词为单位反转
    • 非空格时入栈，否则出栈直到栈空

  • 找亲兄弟，最右边大于自身的为请兄弟，给出每个元素请兄弟下标，没有亲兄弟为-1

    • 初始化输出数组全为-1

    • push(0)

      for(1-----n){

      ​ while(stackempty&&x[stacktop(s)]<=x[i])d[pop(s)]=i;

      ​ push(i,s);

      }

队列

• 指针实现队列
  • 链尾入队
  • 链头出队
• 循环数组实现队列
  • 约定少使用一个节点，元素个数达到maxsize-1时满
  • front指向队首前一个元素
  • 判空front==rear
  • 判满rear+1%maxsize==front
  • 入队（rear+1）%maxsize
  • 出队（front+1）%maxsize
• 主要用于广度优先算法，breadth first serach depth是深度
• split
  • while交叉划分给Q1 Q2
  • 判断Q的最后一个单元是给Q1还是Q2，如果给Q1要给Q2的rear->next =0；
• combine
  • 合并为Q
  • Q1Q2判空，空直接制作好Q返回
  • 交叉合并
  • 判剩余
• 双端队列
  • 循环数组实现双端队列
    • 四个操作，头部插入、删除，尾部插入、删除
    • 分别要写四个enter，和delete
  • 指针实现双端双链表
    • 也是写四个操作

排序

• 冒泡排序 bubble

• 插入排序 insertion

• 选择排序 select

  • 简单排序时间复杂度都是n^2 空间复杂度都是O1

• 快速排序 quick

  • 第一个或最后一个座位基准元素，最坏时n方
  • 空间复杂度nlogn与时间复杂度相同
  • 要使quick最坏时间复杂度能达到nlogn就耀在On时间内寻找到中位数median
  • 可使用随机选择基准元素
  • 非递归方式
    • 使用栈技术来代替递归
    • 左右下标入栈
    • while{左右出栈， partition划分，if（i-l>r-i）得出的左右下标又入栈 }
  • 三数取中 加m低于一定时使用普通排序排序子数组
    • 通过交换让array[left]<array[mid]<array[right]
    • partition用right作为基准
  • 三划分
    • 相同元素在中间形成一个数组，设定左右时，以中间数组左右边界为递归的 右左 边界

• 合并排序 merge

  • 常见递归实现
  • 自底向上合并
    • 步长设置m=1，m<=r,m+=m
    • 左边界和次数i=l;i<=r-m;i+=m

• 链表结构合并排序

  • 合并两个有序链表
  • 划分两个链表，一个步长为1，一个步长为2，循环结束步长2停留的指针位置就是mid
  • 队列实现
    • 单链表，打散入队
    • 出队两个使用链表合并得出的一条链表又入队，循环

• 计数排序 count

• 桶排序 bucket

• 基数排序 radix

• 应用举例

  • 最大增序列问题

    • 二维数组每行选择一个数组成一个递增序列

      使用贪心策略，线从最后一行开始选一个最大的，最后一行的最大数决定了递增序列的最大数，自底向上，每行的最大值都要小于上一行的最大值

  • 排序只有 0 1 2的数组

    • 设置三个位置，分成三段，switch，l段以m段开头作为结尾，r段从后向前，循环以m<=r 结束

  • 数值范围限制时用桶排序或基数排序

  • 众数

    • 直接使用count数组进行统计，数值需要有范围

  • 最优服务次序，让服务平均等待时间最小

    • 每个客户的等待时间是前面顾客的总和
    • 升序排序，从头叠加到尾部，/个数计算平均时间

树

• 根节点，深度为0
• 左儿子右兄弟表示法，
• 满二叉树个数
• 递归遍历
  • While（指针不空），输出，递归左子树，递归右子树
• 非递归遍历
  • 使用栈，while（栈空）「pop输出，左子树入栈，右子树入栈」
• 线索二叉树，叶子节点左子树指向前驱节点，
• 二叉搜索树
• 信号增强布置

题目解法思想

• 删除链表min到max区间的值

  • 思想确定minindex，确定maxindex，两个指针来确定要释放的区间
  • 

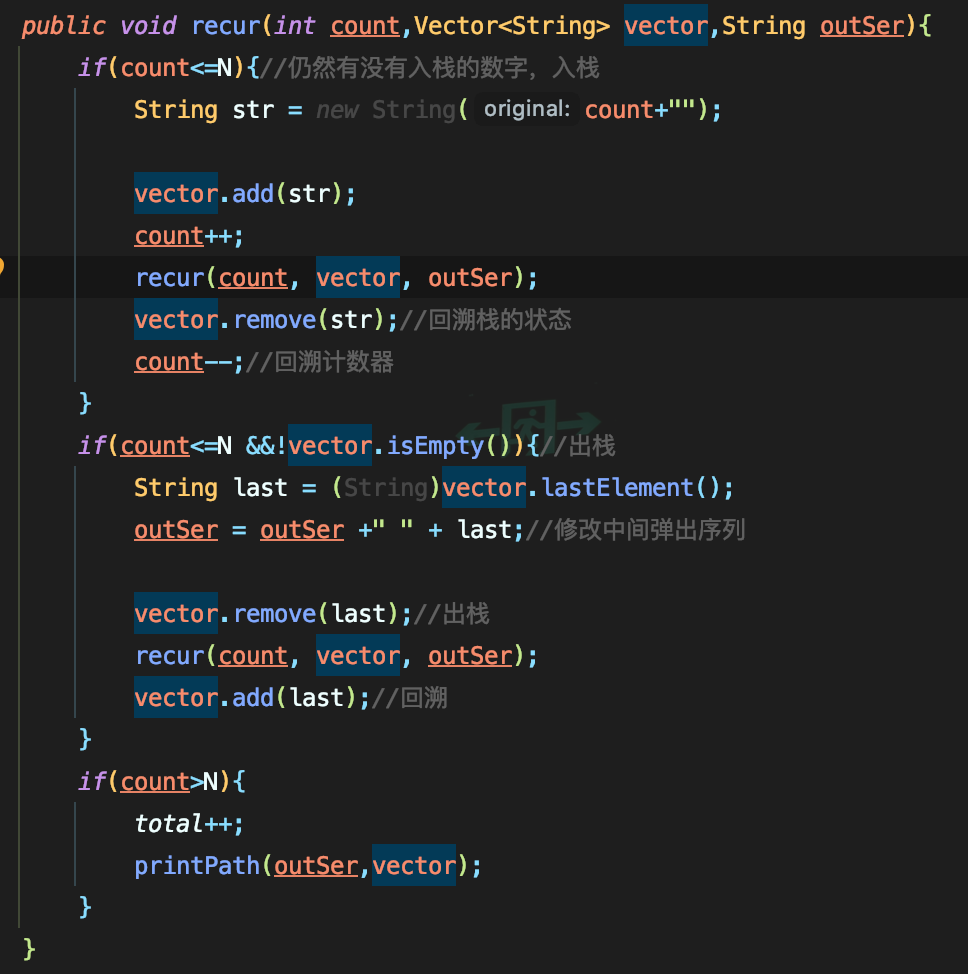
• 给定入栈序列，给出所有的出栈序列

  • 每一次递归有入栈和出栈两种选择，所有数都入栈后就打印，
  • 

• 回文

  • 方法1，使用字符指针指向比较，两头向中比较
  • 方法2，字符串入栈一半，逐个出栈比较

• 是否是合法序列

• 可以用两个变量分别记录入栈和出栈，循环范围为输入数组长度，如果是 I就i++如果是O就 j++，O操作只要i<j 就直接为非法序列并且exit，循环结束 i！=j 说明入栈和出栈次数不一，也是非法，else 合法

• 带头节点的循环链表表示队列，设置一个指针指向队尾元素站点，设置队空，判队空，入队，出队

  • 

  • 和书本中的初始化一样，分配一个表头节点不使用

  • 从rear->指向的是表头节点，不存储东西的，结构是和书中的一样rear的位置是表尾巴，rear->next->next 是表头

  • #include <stdio.h>#include "stdlib.h"typedef struct  queuenode{	int data;	struct queuenode * next;	}QueueNode;typedef  struct {	QueueNode * rear;	}linkQueue;void insertNode(linkQueue *Q,int x){	QueueNode * p = malloc(sizeof(QueueNode));	p->data = x;	p ->next = Q ->rear ->next;	Q->rear ->next  = p;	Q ->rear = p;	}int emptyQueue(linkQueue *Q){	return Q->rear ->next->next == Q->rear->next;}linkQueue * initQueue(void){	linkQueue * L = malloc(sizeof(linkQueue));	QueueNode * node = malloc(sizeof(QueueNode));	//注意malloc一个node然后再让link的指向	L->rear = node;	L->rear->next = L->rear;//指向自己	return L;}void printqueue(linkQueue * Q){	QueueNode *p;	p = Q->rear ->next->next;	//从节点开始遍历，p=p->next 指向，那个表头节点空节点时，刚好遍历完最后一个标为节点，rear，所以应该在rear->next时候停下	while (p!=Q->rear->next) {		printf("%d ",p->data);		p=p->next;	}	}int deleteQueue(linkQueue *Q){	QueueNode *p;	p = Q ->rear ->next->next;	//先判空，然后从表头删除，指向表头节点的位置	if(emptyQueue(Q)){		printf("link NULL");		return -1;	}	int x = p->data;		if(p == Q->rear){		//最后一个节点		//要移动指针和rear的位置，使rear的位置停留在表头节点（空节点），指向也好指向自己		Q->rear = Q ->rear->next;		Q->rear->next = Q->rear;	}else {		Q ->rear ->next->next = p->next;		//改变指向，确定了新的头节点	}		free(p);	return x;}int main(int argc, char *argv[]) {	linkQueue * Q;	Q = initQueue();	insertNode(Q, 1);	insertNode(Q, 2);	insertNode(Q, 3);	deleteQueue(Q);	printqueue(Q);}
    

  • 

• 使用tag 为0和tag为1表示front和rear相等时为空还是满

  • 队首删除，队尾插入

  • 初始front=rear=tag=0

  • isEmpty return (front==rear && tag == 0);//为空返回1isFull return (front==rear && tag == 1);//full ret 1EnQueue  if(!isFull){    //不满的前提下能插入    rear = (rear+1)%length;    if(rear == front) tag = 1;  }else{    exit(0);  }DeQueue  //同理,但是要返回front的值  getFront  if(!isEmpty){   	return array[ (front+1)%10 ];  }else{   	print。。  }
    

• 循环数组实现队列，要求从 rear删除，从front插入

  • [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-m2IjK9xU-1629271689941)(…/…/…/Library/Application Support/typora-user-images/image-20210318235106302.png)]

  • 解题关键在于初始化

    • 这样是理解错误的，rear向右++，front向左–，方向应该一致，像正常的从尾巴插入，从头删除，是rear++，front++

    • 改成从尾删除，从头插入，就要是rear–，front–，这里用到了–从头转到尾巴的方法就是（front-1+M）%M 能使指针指向尾部

    • #include <stdio.h>#include "stdlib.h"#define   M 5typedef struct queue{	int array[M];	int front;	int rear;	}Queue;void InQueue(Queue * Q,int x){	if(Q->rear == (Q->front-1+M)%M){			printf("full ");				}else {		Q->array[Q->front] = x;		Q->front  = (Q->front-1+M)%M;				}}int DeQueue(Queue *Q){	//rear 删除 向左	if(Q->front == Q->rear){		printf("Empty");		return -1;		}else {		Q->rear  =  (Q->rear-1+M)%M;		return Q->array[(Q->rear+1+M)%M];			}}int main(int argc, char *argv[]) {	Queue * Q ;	Q = malloc(sizeof(Queue));	Q->front =0;	Q->rear = 0;	InQueue(Q, 1);	InQueue(Q, 2);	InQueue(Q, 3);	printf("%3d",DeQueue(Q));	printf("%3d",DeQueue(Q));	printf("%3d",DeQueue(Q));	printf("%3d",DeQueue(Q));	}
      

    • front 和rear的位置唯一的要求就是要一致

    • 要注意的地方，rear删除要不然提前将这个位置的数据记录好，再移动，后续好返回记录好的数据，跟普通的链表同理，front指向的是表头的前一个位置，rear要删除也是在前一个位置，移动了就要将上一个位置返回，而不是移动后的位置

• 单链表实现选择排序

  • 交换指针太复杂，两个for交换数据项就行